Расчет потока вектора Умова-Пойтинга

Оценим величину мощности потерь электромагнитной энергии, вытекающей через боковую поверхность той части объема пластины, которая находится внутри зазора.

Вектор Умова - Пойтинга параллелен плоскости пластины, поэтому

Найдём сначала поток этого вектора через боковые грани, перпендикулярные оси (рис.2)

Рис.2. К расчёту потока энергии через боковую поверхность той части объёма пластины, который находится внутри зазора.

(16)

Как и раньше, множитель соответствует средней мощности потерь за период.

Электромагнитное поле на поверхности

(17)

На поверхности

(18)

Используя выражения (17) и (18) в подынтегральном выражении (17) и учитывая направления внешних нормалей к поверхностям и , в результате интегрирования получим

, (19)

где - средний радиус тороида. Результат (19) следует удвоить за счет электромагнитной энергии, поступающей в пластину сверху.

Аналогично вычислим поток вектора-Пойтинга через боковые грани, перпендикулярные оси , На поверхности ( )

(20)

Очевидно, на поверхности

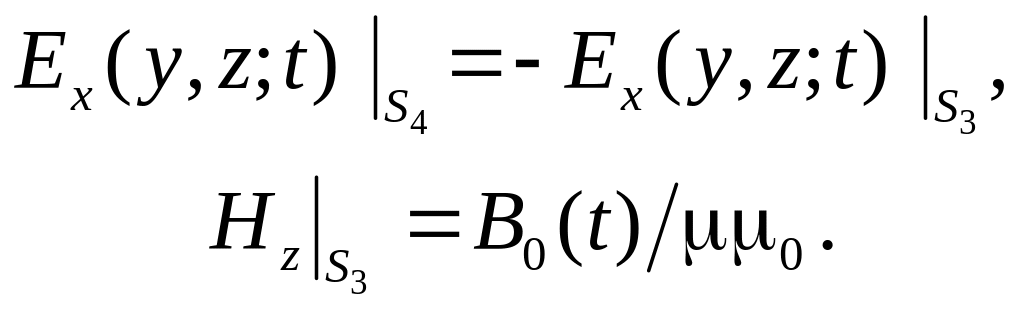(21)

Из соображений симметрии потока вектора Пойтинга через поверхности и равны. Суммарный поток через эти поверхности равен

. (22)

Этот результат следует удвоить, учитывая электромагнитную энергию, поступающую в пластину сверху.

Полная средняя мощность , теряемая в той части объёма пластины, которая находится вне зазора, оказывается равной

(23)

Сравнивая формулу (23) с (15), оценим, какую часть эта энергия составляет от энергии джоулевых потерь внутри зазора

(24)

В случае сильного скин-эффекта ( - глубина скин-слоя на много меньше толщины пластины и тем более ) получим

(25)

Для слабого пьезоэффекта и тем более , разлагая в ряд экспоненту в формуле (24)

,

получим

(26)

Из формулы (25) следует, что в случае сильного скин-эффекта потерями в объёме пластины вне зазора, можно пренебречь. Наоборот, если скин-эффект отсутствует, то согласно формуле (26), в этот объём излучается энергия, которая на много больше энергии джоулевых потерь внутри зазора. Поэтому для пластин с малой проводимостью величина в (26) может соответствовать добротности, которая окажется больше добротности датчика без пластины, и её будет невозможно зафиксировать.

Интервал измерений проводимости бесконтактным методом снизу не связан со скин-эффектом, он ограничен величиной добротности датчика без пластины. Сверху этот интервал ограничен скин-эффектом, когда для пластин с большой проводимостью в тонком скин-слое джоулевы потери оказываются также настолько малыми, что соответствующая им добротность меньше добротности датчика без пластины.

Методика измерения проводимости q-метром

Проведенное теоретическое исследование позволяет обосновать следующую методику измерений. Поскольку неизвестны параметры ферритового датчика, джоулевы потери в обмотке, потери на излучение и т.д., предлагается вначале измерить величину - добротность ферритового датчика без пластины, затем - добротность датчика с эталонной пластиной, проводимость которой считается известной, и, наконец, - добротность пластины, проводимость которой требуется определить

Составим систему трех уравнений

(27)

Здесь W - полная электромагнитная энергия эквивалентного резонансного контура, - джоулевы потери эталонного образца, - джоулевы потери образца, проводимость которого нужно определить.

Из системы уравнений (13) найдем величину отношения

(28)

С другой стороны, из выражения (15) для энергии джоулевых потерь следует . (29)

Приравнивая правые части выражений (28) и (29), получим формулу для вычисления

. (30)