5 Результаты расчета.
Решение, полученное средствами обоих пакетов, совпадает, что подтверждает правильность выполненных расчетов.
Решение позволяет ответить на ряд вопросов о характере распределения температуры в области.
Температура возрастает в области получения решения монотонно на большей части области полученных значений, без разрывов (рисунок 5.1). Но при увеличении времени температура убывает при t=0,1с и t=0,2с, особенно при малых значениях пространственных координат (при t=0,2с это наблюдается лишь при x до 0,5м). Температурные профили в эти моменты времени представлены на рисунках 5.2 и 5.3.
Можно определить наименьшую и наибольшую температуру и их расположение в области, например как на рис. 5.4. Максимум наблюдается при x=0,75м и t=1,1c, а минимум – при x=0,15м и t=0,2c.
Можно проследить распределение температуры в определенный момент времени (например, как на рис. 5.5), а также изменение температуры в некоторой точке области за рассмотренный промежуток времени (например, как на рис. 5.2). С увеличением координаты температура монотонно возрастает при t=0,9c; при увеличении времени до 0,1с температура убывает, а затем монотонно возрастает при x=0,6
Рисунок 5.1. График поверхности распределения температуры.
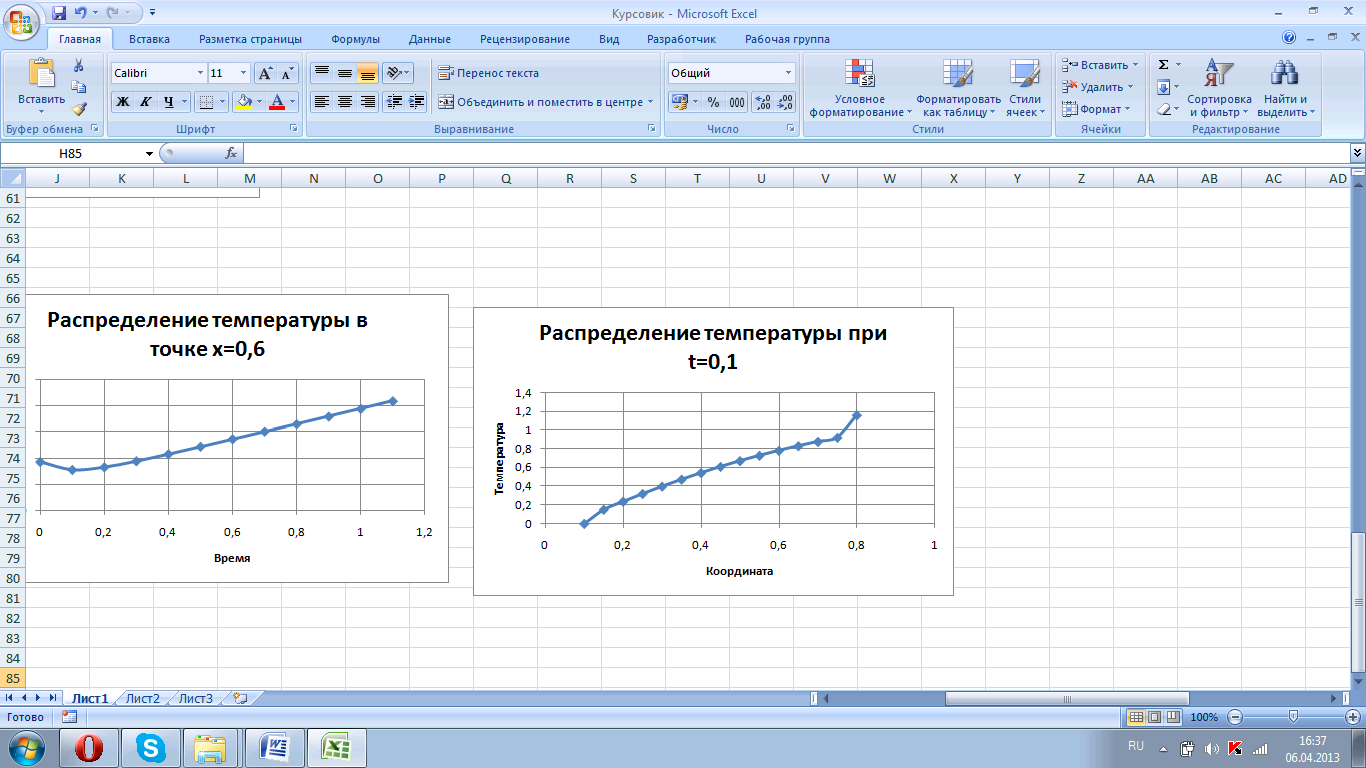
Рисунок 5.2. Температурный профиль в момент времени t=0,1.
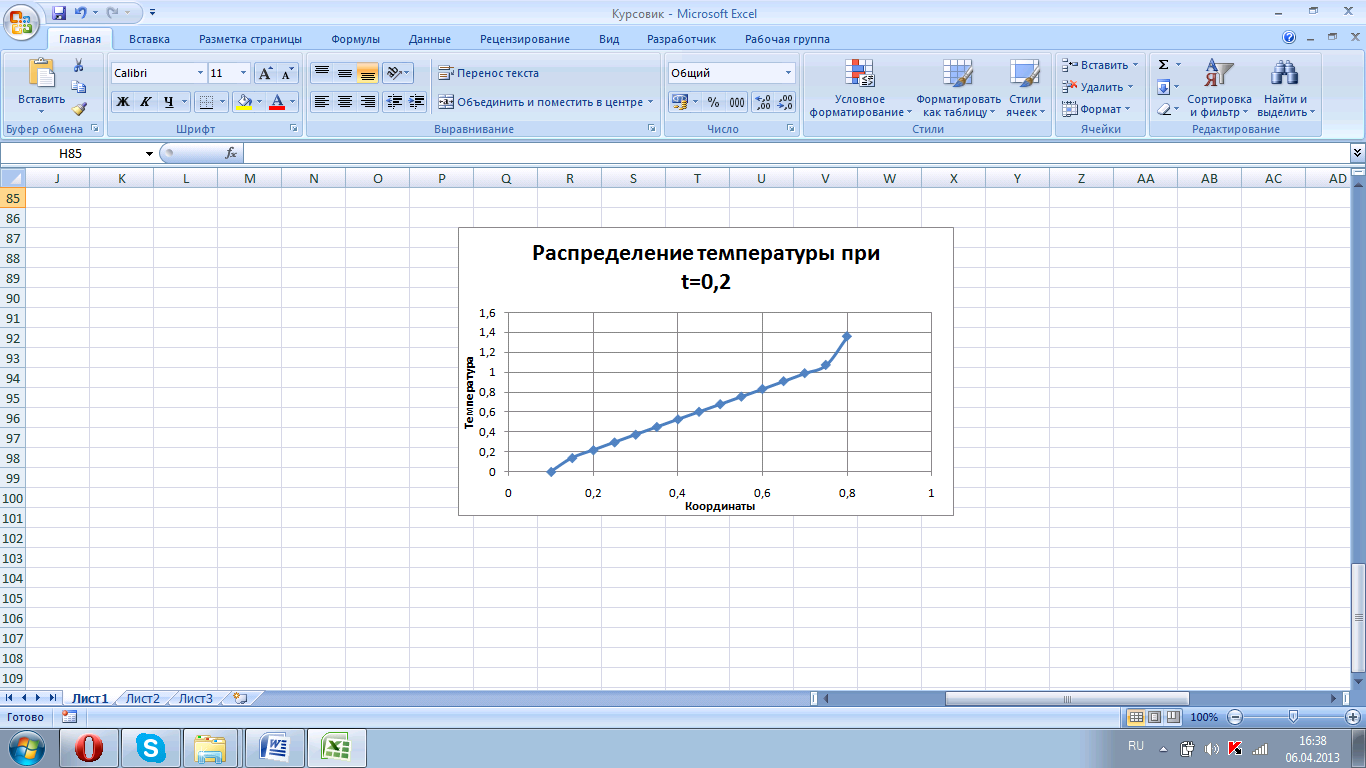
Рисунок 5.3. Температурный профиль в момент времени t=0,2.
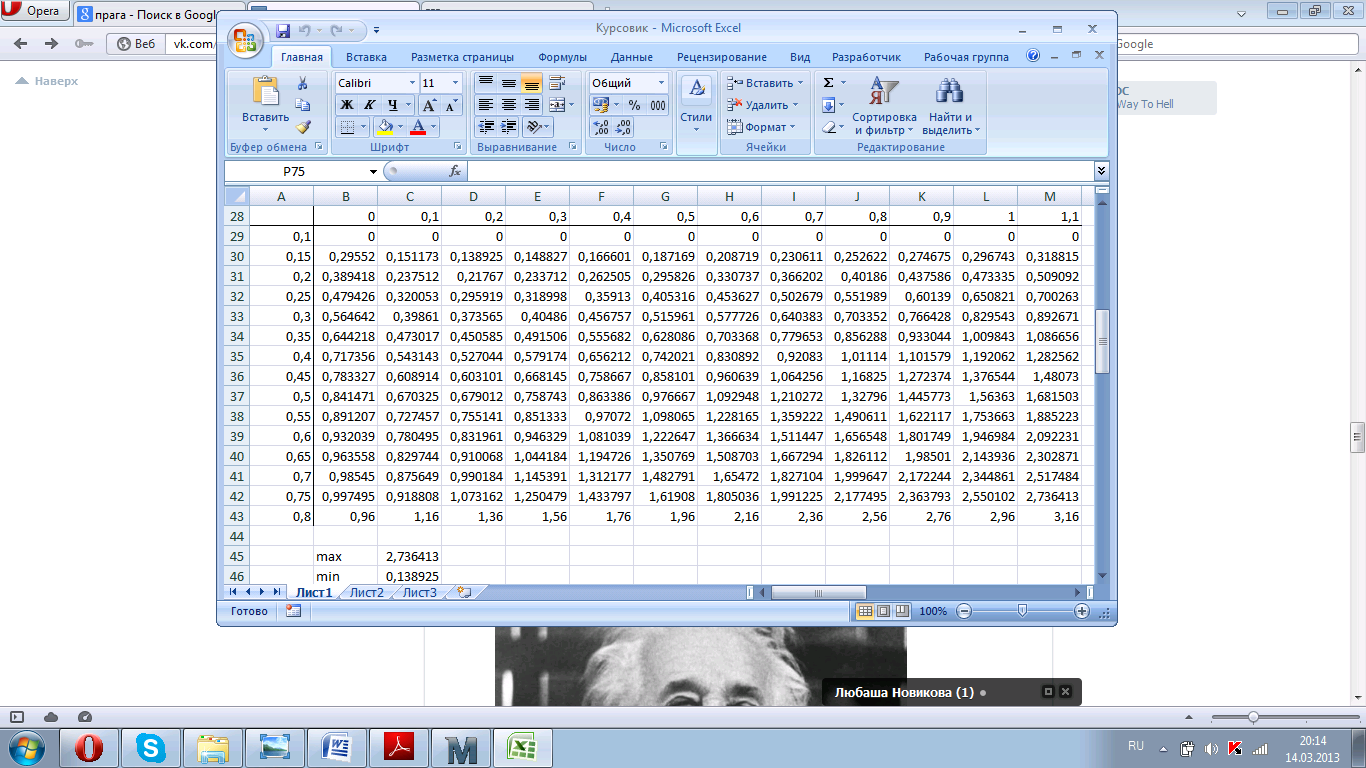
Рисунок 5.4. Анализ решения на максимальное и минимальное значения.
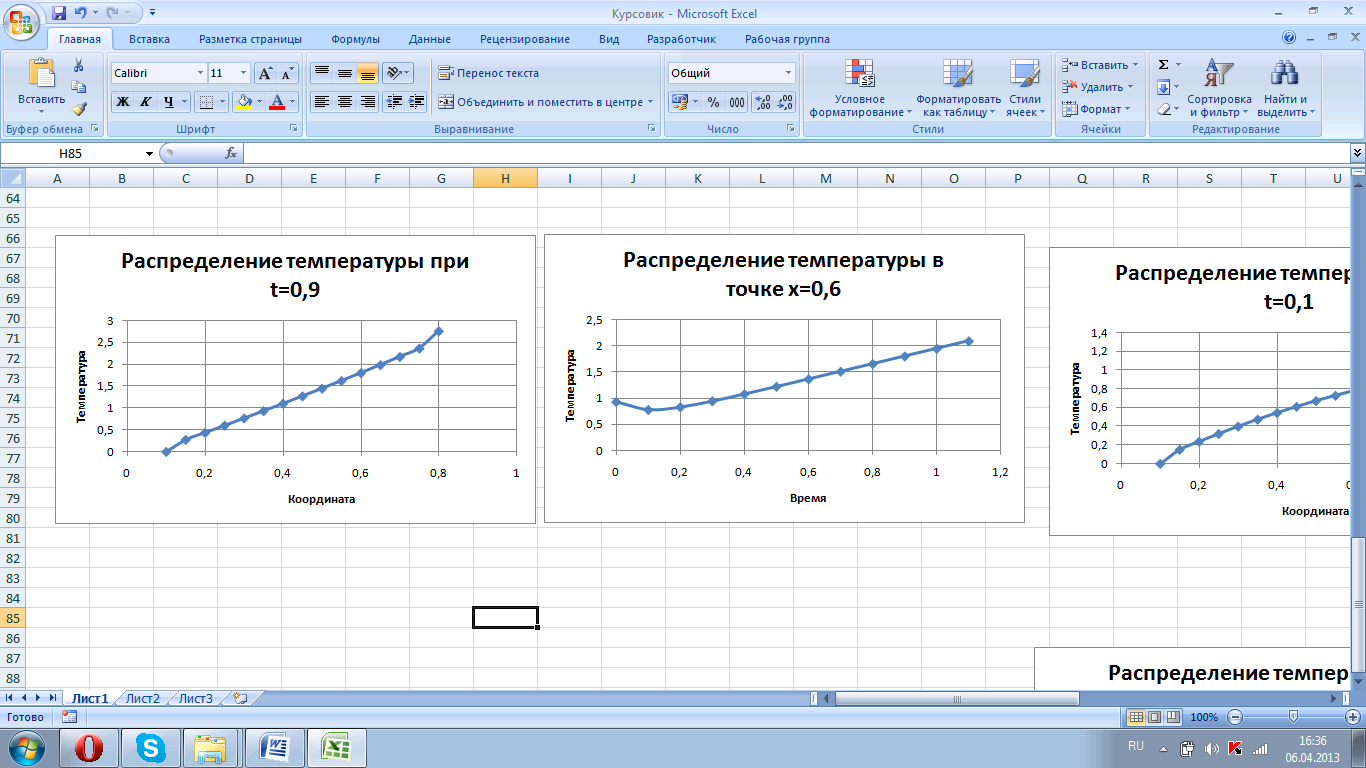
Рис. 5.5. График изменения температуры (температурные профили) в момент времени t=0,9 и график изменения температуры в точке x=0,6.
Вывод:
Наиболее быстро температура возрастает на последнем временном слое (t=1,1с), наименее быстро на первом временном слое (t=0). В зависимости от координаты температура наиболее быстро возрастает при x=0,8м, а наиболее медленно при x=0,1 м, точнее, там она даже не изменяется.
Небольшое отклонение при t=0,1с и 0,2с на фоне общей монотонности связано с возможной некорректностью начальных и граничных условий.
6 Заключение.
В ходе работы мне удалось по достоинству оценить преимущества пакетов MathCad и Ms Excel. Выполнение сложных вычислений с использованием этих пакетов существенно облегчает задачу и экономит время. Также, используя, эти пакеты мы уменьшаем риск возникновения вычислительной ошибки.
Таким образом, выполнять численное моделирование распределения теплопереноса в этих пакетах довольно удобно, а полученные результаты отличаются хорошей точностью.
7 Список литературы и источников.
1. Бронштейн И.Н., Семендяев Н.А. Справочник по математике для инженеров и учащихся втузов.
2. Быкова О.Г. Информатика. Решение нелинейных и дифференциальных уравнений: методические указания к выполнению практических и лабораторных работ. СПб, 2009.- 70 с.
3. Быкова О.Г. Информатика. Вычисления в Microsoft Excel: методические указания к самостоятельной работе. СПб, 2008.- 58 с
4. Быкова О.Г. Применение программных продуктов для прикладных задач математического моделирования: Учебное пособие. СПб, Национальный минерально-сырьевой университет «Горный», 2012.- 58 с.
5. Половко А.М., Ганичев И.В. MathCAD для студента.- СПб.: БХВ-Петербург, 2006.- 336 с.
6. Калиткин Н.Н. Численные методы. М.: Наука, 1978.- 522 с.
7. Правила оформления курсовых и квалификационных работ. Методические указания /Сост. И.О.Онушкина, П.Г. Талалай .- СПб.: СПГГИ, 2005.-64 с.
8. Самарский А.А. Лекции по теории разностных схем. М.: изд-во АН СССР, 1969.- 447 с