6. Метод наименьших квадратов в регрессионном анализе.

В общем случае задача метода наименьших квадратов формулируется следующим образом. Пусть искомая функциональная зависимость величины у от величины х выражается формулой:

           (1)

где заданные функции, искомые параметры – коэффициенты уравнения (1). Предполагается, что значения аргумента  х  установлены точно, а соответствующие значения функции  у  определены в эксперименте с некоторой погрешностью. Если бы измерения производились без ошибок, то для определения параметров  потребовалось бы ровно  т+1  измерений. Но из-за ошибок эксперимента разные серии из  т+1  измерений будут давать различные значения параметров . Поэтому количество проводимых измерений должно быть гораздо бо’льшим, чем число  т  определяемых параметров, для уменьшения влияния ошибок  эксперимента за счет использования избыточной информации и получения наилучших в некотором смысле оценок определяемых параметров.  Итак, для получения оценок параметров проводят  n  экспериментов, результаты которых дают значения не этих параметров, а некоторой функции (1), зависящей от них линейно.

Метод наименьших квадратов состоит в том, что оценки параметров формулы (1) определяются из условия: сумма квадратов отклонений

         (2)

достигает наименьшего значения.

Для определения этих оценок нужно продифференцировать (2) по всем оценкам , приравнять все производные нулю и решить полученную линейную систему из т+1 уравнений относительно т+1 неизвестных оценок параметров :

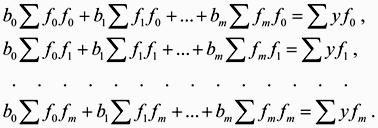           (3)

Система уравнений (3) называется системой нормальных уравнений Гаусса. Здесь для краткости записи приняты следующие обозначения сумм:

       (4)

Следует отметить, что система уравнений (3) иногда оказывается плохо обусловленной, т.е. ее решения весьма чувствительны к малейшим изменениям в результатах измерений. Для плохо обусловленных систем в настоящее время разработаны специальные методы, например, метод регуляризации.

7. Линейная модель регрессии.

Линейная регрессия (англ. Linear regression) — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости.

Модель линейной регрессии является часто используемой и наиболее изученной в эконометрике. А именно изучены свойства оценок параметров, получаемых различными методами при тех или иных предположениях о вероятностных характеристиках факторов и случайных ошибок модели. Предельные (асимптотические) свойства оценок нелинейных моделей также выводятся исходя из аппроксимации последних линейными моделями. Необходимо отметить, что с эконометрической точки зрения более важное значение имеет линейность по параметрам, чем линейность по факторам модели.

Общая модель линейной регрессии

Введем два вектора: —факторы регрессии и -- неизвестные параметры регрессии. Каждый вектор есть вектор-столбец, а изображен по горизонтали для удобства. Обозначать вектора мы, как и ранее, будем жирным шрифтом.

Рассматривается модель регрессии, которая в курсе «Эконометрика» называется простой (линейной) регрессией:

Пусть в -м эксперименте факторы регрессии принимают заранее заданные значения , где .

После экспериментов получен набор откликов , где

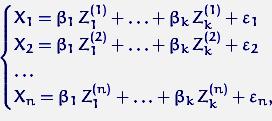
или, в матричной форме, , где матрица (матрица плана) равна

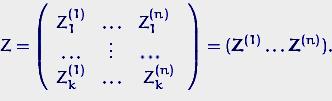
Вектор состоит из случайных ошибок в данных экспериментах.

Требуется по данным матрице плана и вектору результатов найти оценки для параметров регрессии и параметров распределения вектора ошибок .