35. Доверительные интервалы для прогнозируемых значений временных рядов.

Очевидно, что точность прогноза тем выше, чем меньше величина ошибки, которая представляет собой разность между прогнозируемым и фактическим значением исследуемой величины.

Вся проблема состоит в том, чтобы вычислить ошибку прогноза, так как фактическое значение прогнозируемой величины станет известно только в будущем. Следовательно, методы оценки точности по уже свершившимся событиям (апостериорные) не имеют практической ценности, так как являются лишь констатацией факта. При разработке прогноза оценку его точности требуется производить заранее (априорно), когда истинное значение прогнозируемой величины еще не известно. Как же поступить в этих случаях? Дискуссии в специальной литературе отмечают эти трудности, и в итоге все предложения так или иначе связаны с определением доверительного интервала на основе статистического выборочного метода. При этом точность прогноза оценивается величиной доверительного интервала для заданной вероятности его осуществления, а под достоверностью понимают оценку вероятности осуществления прогноза в заданном доверительном интервале. Таким образом, точность прогноза выражается с помощью вероятностных пределов фактической величины от прогнозируемого значения.

Следует отметить, что точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, явление маловероятное. И этому виной следующие источники погрешностей:

1) выбор формы кривой (порядка полинома и т. д.), характеризующей тренд, содержит элемент субъективизма. Во всяком случае, часто нет твердой основы для того чтобы утверждать, что выбранная форма кривой является единственно возможной или тем более наилучшей для экстраполяции в данных конкретных условиях;

2) оценивание параметров кривых (иначе говоря, оценивание тренда) производится на основе ограниченной совокупности наблюдений, каждое из которых содержит случайную компоненту. В силу этого параметрам кривой, а следовательно, и ее положению в пространстве свойственна некоторая неопределенность;

3) тренд характеризует некоторый средний уровень ряда на каждый момент времени. Отдельные наблюдения, как правило, отклонялись от него в прошлом. Естественно ожидать, что подобного рода отклонения будут происходить и в будущем.

Погрешность, связанная со вторым и третьим ее источниками, и может быть отражена в виде доверительного интервала прогноза при принятии некоторых допущений о свойстве ряда.

35. Тест Чоу, его особенности.

Тест Чоу может применяться, например, для выявления стабильности временного ряда. Для этого временной ряд разбивается на две подвыборки: до существенных изменений ряда и после этого. Выдвигается гипотеза о структурной стабильности тенденции ряда и проверяется на основании теста Чоу.

В практике эконометрики нередки случаи, когда имеются две выборки пар значений зависимой и объясняющих переменных ( ). Например, одна выборка пар значений переменных объемом получена при одних условиях, а другая, объемом — при несколько измененных условиях. Необходимо выяснить, действительно ли две выборки однородны в регрессионном смысле. Другими словами, можно ли объединить две выборки в одну и рассматривать единую модель регрессии по ?

При достаточных объемах выборок можно было, например, построить интервальные оценки параметров регрессии по каждой из выборок и в случае пересечения соответствующих доверительных интервалов сделать вывод о единой модели регрессии. Возможны и другие подходы.

В случае, если объем хотя бы одной из выборок незначителен, то возможности такого (и аналогичных) подходов резко сужаются из-за невозможности построения сколько-нибудь надежных оценок.

В критерии {тесте) Г. Чоу эти трудности в существенной степени преодолеваются.

1.По каждой выборке строятся две линейные регрессионные модели:

Проверяем гипотезу

2. Рассчитываем суммы квадратов остатков для регрессий.

3. Строим регрессию.

4. Рассчитывается :

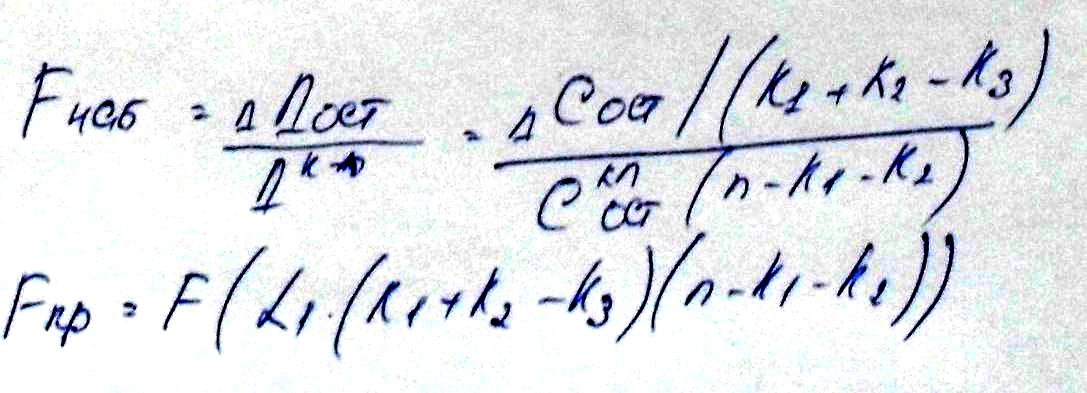
Если F наб. попадает в интервал распределения, то нулевая гипотеза отвергается и мы не можем объединить две выборки в одну

Если нулевая гипотеза верна, то две регрессионные модели можно объединить в одну.

Идея теста Чоу тесно связана с методикой регрессионного анализа с фиктивными переменными, когда имеется возможность разделения совокупности на­блюдений по степени воздействия этого фактора на отдельные группы и требуется установить возможность использования единой модели регрессии.

Оценивание регрессии с использованием фиктивных переменных более информативно в том отношении, что позволяет использовать -критерий для оценки существенности влияния каждой фиктивной переменной на зависимую переменную.

Особенности:

1. Если число параметров уравнения регрессии (Ia, Ib, II) имеют одинаковое количество, то формула для расчета наблюдаемого значения упрощаются.

2. Тест Чоу позволяет сделать вывод о наличии или отсутствии структурной стабильности в изучаемом временном ряду. Если наблюдаемое значение не превосходит критического значения Фишера, то уравнения Ia, Ib описывают одну и ту же тенденцию, а различие числовых оценок их параметров а_1, а₂ и b₁ b₂ соответственно статистически не значимы. В обратном случае – гипотеза структурной стабильности отклоняется, что означает статистическую значимость различия оценок параметров Ia и Ib.

Применение теста Чой предполагает соблюдение предпосылок о нормальном распределении остатков в уравнениях Ia и Ib и независимость их распределения. Если гипотеза о структурной стабильности тенденции временного ряда отклоняется, то дальнейший анализ заключается в дальнейшем исследовании и более детальном рассмотрении характера изменения тенденции.