Декартово произведение двух множеств обладает следующими свойствами:

• A×B ≠ B×A–некоммутативность

• A× (B×С) = (A×B) ×C= A×B×C – ассоциативность

• A× (B C) = (A×B) (A×C) – дистрибутивность по объединению

• A× (B C) = (A× B) (A× C) – дистрибутивность по пересечению

• A× (B\C) = (A×B)\( A×C)– дистрибутивность по разности

• (A × B) (C × D)=(A C)×(B D)

Теорема.

Число всех подмножеств множества A из n элементов равно

Следствие. Справедливо равенство

поскольку число k - элементных подмножеств множества из n элементов, то сумма в левой части есть число всех подмножеств.

Свойства счетных множеств

а) Объединение конечного числа счетных множеств счетно

б) Объединение счетного числа счетных множеств счетно

в) Объединение конечного числа конечных множеств конечно или счетно

Теорема. Пусть А и В счетные множества. Тогда декартово произведение  также является счетным множеством.

Доказательство. Перечислим элементы множеств А и В: А= ,  Тогда  =  Разобьем  на счетное объединение счетных множеств:

,

,

.…………………………………….

.

Очевидно, что Ø при , т.к. , и =А В, то есть  есть объединение счетного числа счетных попарно непересекающихся множеств. Значит  счетно.

Следствие. Пусть  – счетные множества, тогда  – счетно.

Теорема. Отрезок равномощен множеству всех бесконечных последовательностей нулей и единиц.

Доказательство. В самом деле, каждое число записывается в виде бесконечной двоичной дроби. Первый знак этой дроби равен или в зависимости от того, попадает ли число в левую или правую половину отрезка. Чтобы определить следующий знак, надо выбранную половину поделить снова пополам и посмотреть, куда попадет , и т.д.

Это же соответствие можно описать в другую сторону: последовательности соответствует число, являющееся суммой ряда

Описанное соответствие пока что не совсем взаимно однозначно: двоично-рациональные числа (дроби вида ) имеют два представления. Например, число можно записать как в виде , так и в виде Соответствие станет взаимно однозначным, если отбросить дроби с единицей в периоде (кроме дроби , которую надо оставить). Но таких дробей счетное число, поэтому на мощность это не повлияет.

Теорема. Квадрат (со внутренностью) равномощен отрезку.

Доказательство. Квадрат равномощен множеству пар действительных чисел, каждое из которых лежит на отрезке (метод координат). Мы уже знаем, что вместо чисел на отрезке можно говорить о последовательностях нулей и единиц. Осталось заметить, что паре последовательностей нулей и единиц можно поставить в соответствие последовательность-смесь и что это соответствие будет взаимно однозначным.

Теорема. Если множество бесконечно, а множество конечно или счетно, то объединение равномощно .

Доказательство

Можно считать, что не пересекается с (пересечение можно выбросить из , останется по-прежнему конечное или счетное множество).

Выделим в счетное подмножество ; остаток обозначим через . Тогда нам надо доказать, что равномощно (знак символизирует объединение непересекающихся множеств). Поскольку и оба счетны, между ними существует взаимно однозначное соответствие. Его легко продолжить до соответствия между и (каждый элемент множества соответствует сам себе).

Неравенство мощностей

Отношение " иметь не большую мощность" обладает свойствами:

• Если и равномощны, то имеет не большую мощность, чем . (Очевидно.)

• Если имеет не большую мощность, чем , а имеет не большую мощность, чем , то имеет не большую мощность, чем . (Пусть находится во взаимно однозначном соответствии с , а находится во взаимно однозначном соответствии с . Тогда при втором соответствии 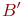соответствует некоторому множеству , как показано на рис, и потому равномощно .)

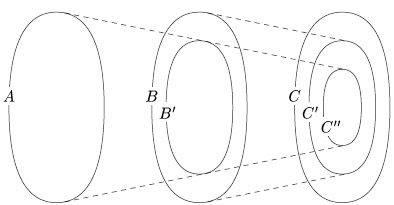
Рис. Транзитивность сравнения мощностей

• Если имеет не большую мощность, чем , а имеет не большую мощность, чем , то они равномощны. (Это утверждение составляет содержание теоремы Кантора - Бернштейна)

• Для любых двух множеств и верно (хотя бы) одно из двух: либо имеет не большую мощность, чем , либо имеет не большую мощность, чем .

Теорема. (Кантора-Бернштейна) Если множество равномощно некоторому подмножеству множества , а равномощно некоторому подмножеству множества , то множества и равномощны.

Доказательство

Пусть равномощно подмножеству множества , а равномощно подмножеству множества .

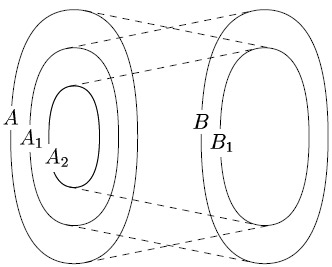Рис.

 

При взаимно однозначном соответствии между и подмножество переходит в некоторое подмножество . При этом все три множества , и равномощны, - и нужно доказать, что они равномощны множеству , или, что то же самое, .

Теперь можно забыть про множество и его подмножества и доказывать такой факт:

если и равномощно , то все три множества равномощны.

(Для единообразия будем говорить вместо .)

Пусть - функция, осуществляющая взаимно однозначное соответствие (элемент соответствует элементу ). Когда переходит в , меньшее множество переходит в некоторое множество (см. рис. ниже)). Аналогичным образом само переходит в некоторое множество . При этом , так как .

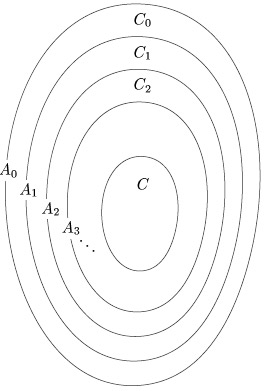Рис.  

Продолжая эту конструкцию, получаем убывающую последовательность множеств

и взаимно однозначное соответствие , при котором соответствует (иногда это записывают так: ). Формально можно описать как множество тех элементов, которые получаются из какого-то элемента множества после -кратного применения функции . Аналогичным образом состоит из тех и только тех элементов, которые получаются из какого-либо элемента множества после -кратного применения функции .

Заметим, что пересечение всех множеств вполне может быть непусто: оно состоит из тех элементов, у которых можно сколько угодно раз брать - прообраз. Теперь можно сказать так: множество разбито на непересекающиеся слои и на сердцевину .

Слои , , , равномощны (функция осуществляет взаимно однозначное соответствие между и , между и и т.д.):

То же самое можно сказать про слои с нечетными номерами:

Можно отметить, что функция на множестве осуществляет его перестановку (взаимно однозначное соответствие с самим собой).

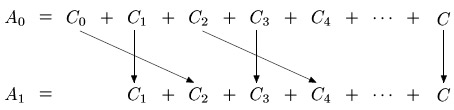Построим взаимно однозначное соответствие между и . Пусть . Тогда соответствующий ему элемент строится так: при и при или (см. рис.)

Рис. 

Теорема Кантора-Бернштейна значительно упрощает доказательства равномощности: например, если нужно доказать, что бублик и шар в пространстве равномощны, то достаточно заметить, что из бублика можно вырезать маленький шар (гомотетичный большому), а из шара - маленький бублик.

При сравнении мощностей для заданных множеств и теоретически имеются четыре возможности:

• равномощно некоторой части , а равномощно некоторой части . (В этом случае множества равномощны.)

• равномощно некоторой части , но не равномощно никакой части . В этом случае говорят, что имеет меньшую мощность, чем .

• равномощно некоторой части , но не равномощно никакой части . В этом случае говорят, что имеет большую мощность, чем .

• Ни не равномощно никакой части , ни не равномощно никакой части . Этот случай невозможен.

Теорема Кантора

Множество бесконечных последовательностей нулей и единиц несчетно.

Доказательство

Предположим, что оно счетно. Тогда все последовательности нулей и единиц можно перенумеровать: Составим бесконечную вниз таблицу, строками которой будут наши последовательности:

(через мы обозначаем -й член -й последовательности). Теперь рассмотрим последовательность, образованную стоящими на диагонали членами , , , ; ее -й член есть и совпадает с -м членом -й последовательности. Заменив все члены на противоположные, мы получим последовательность , у которой

так что последовательность отличается от любой из последовательностей (в позиции ) и потому отсутствует в таблице. А мы предположили, что таблица включает в себя все последовательности - противоречие.

Теорема 3 (обобщенная теорема Кантора). Для любого множества А имеет место неравенство  (Никакое множество не равномощно множеству всех своих подмножеств).

Доказательство. Докажем, что  Построим вложение А в Р(А):  Очевидно, что f - искомое вложение.

Докажем, что между А и Р(А) не существует биекции. Доказываем от противного. Допустим, что существует биекция F: AP(A). Отметим, что для каждого хА F(х) поэтому для каждого х уместно поставить вопрос: хF(x) или хF(x)?

Элемент х назовем «хорошим», если хF(x). Пусть  - множество всех «плохих» элементов из А. Так как F по допущению есть отображение «на», то существует х₀А такой, что F(х₀)=Х₀. Возникает вопрос, х₀-«плохой» или «хороший»?

Если х₀ «хороший», то х₀F(x₀), значит х₀X₀, то есть х₀F(x₀) и х₀ «плохой». Противоречие. Значит х₀ не может быть «хорошим». Ему остается быть «плохим», то есть х₀F(x₀), поэтому х₀X₀, значит х₀ «хороший». Снова противоречие. Итак, допущение о существовании биекции между А и Р(А) приводит к противоречию. Поэтому  

Эта теорема показывает, что для любого сколь угодно большого множества А существует множество В, мощность которого строго больше А. То есть последовательность мощностей ничем не ограничена.