 И.Ф. Шишкин, В.М. Станякин, 1992

2.ИЗМЕРЕНИЕ КАЧЕСТВА

2.1. Методы измерения показателей качества

Как уже отмечалось (см. п. 1,1), единственный способ по­лучения представления (информации) о количественных характе­ристиках показателей качества — теоретическое или эксперимен­тальное сравнение их размеров между собой.

Сравнение размеров теоретическим путем, как и любое теоре­тическое исследование, не является измерением. Соответственно не является измерительной информацией и представление о размерах, полученное таким путем. Экспериментальное сравнение размеров между собой служит отличительным признаком измерения. На этапе получения измерительной информации экспериментальные данные с целью повыше­ния качества результата измерения могут подвергаться математи­ческой обработке. Однако в дальнейшем, после получения резуль­тата измерения, никакое его преобразование и использование, г. е. переработка измерительной информации, измерением не яв­ляется.

Противоположная точка зрения состоит в том, что рассмотрен­ное измерение называется прямым, а переработка измерительной информации, полученной в результате прямых измерений, в зави­симости от ее вида называется косвенным, совокупным или сов­местным измерением. При таком подходе стирается грань между получением и использованием измерительной информации, меж­ду измерениями и вычислениями, между теоретическим и экспери­ментальным методами исследований.

Получение представления (информации) о размерах теорети­ческим путем будем называть расчетным методом определения по­казателей качества. Он может основываться как на теоретических исходных данных (каких-либо научных положениях, обозначениях размеров), так и на конкретных результатах измерений.

Получение представления (информации) о количественных ха­рактеристиках показателей качества опытным путем (эксперимен­тально) называется измерением. Результат измерения будем рас­сматривать как форму представления измерительной информации.

Измерения могут выполняться как с помощью специальных технических средств, имеющих нормированные метрологические характеристики (они называются средствами измерений), так и без них. Соответственно различаются инструментальный и экс­пертный методы измерений.

Инструментальный метод распространен в технике, в различ­ных сферах народного хозяйства, в области точных и естествен­ных наук. Измерения инструментальным методом могут быть ав­томатическими, автоматизированными либо выполняться вруч­ную.

При автоматических измерениях роль человека полностью ис­ключена (но не на этапе создания средств измерений и методики измерения, конечно). Результат измерений вполне объективный, не зависит от квалификации экспериментатора, настроения, сосре­доточенности и других влияющих на него факторов. Автоматичес­кие измерения обычно бывают высокопроизводительными, резуль­таты их выдаются в форме, удобной для систем автоматического управления, ЭВМ, наглядной для специалистов. Такие измерения являются наиболее ценными в прямом и переносном смысле, ибо стоимость их велика; целесообразность автоматизации измерений должна быть технико-экономически обоснована в каждом от­дельном случае.

При автоматизированных измерениях некоторые измерительные операции (например, считывание показаний, обработку экспери­ментальных данных) выполняет человек. Это существенно снижа­ет качество измерений, делает их менее производительными, но гораздо дешевле. К подготовке операторов, выполняющих изме­рения, предъявляются определенные требования.

Самыми простыми и наиболее распространенными являются измерения вручную. Роль субъективного фактора здесь особенно велика, поэтому работа операторов требует контроля.

Экспертный метод измерений применяют тогда, когда примене­ние более объективных методов с использованием технических средств невозможно, сложно или экономически неоправданно. Очень часто к нему прибегают, например, при визуальной топо­графической съемке, при измерении эргономических и эстетичес­ких показателей качества продукции. Количество экспертов может варьировать от одного до десятков тысяч и даже миллионов. Социологические 'исследования строятся, например, на массовых опросах населения или отдельных его социальных групп, члены которых тем самым выступают в качестве экспертов. Опрос может производиться путем анкетирования, интервьюирования, открыто­го или тайного голосования и т. п. Такие исследования требуют научно обоснованных систем сбора и обработки информации, предполагающих широкое применение средств автоматики и вы­числительной техники. Социологические исследования использу­ются для выяснения общественного мнения, подготовки важных государственных решений (референдум), для определения показателей качества товаров народного потребления {например, спрос) и т. п. В государственном и хозяйственном управлении экс­пертный метод реализуется в форме коллегиальности, в общест­венно-политической жизни — в форме собраний и съездов, в ис­кусстве — в форме жюри, в юриспруденции — в форме судов, в медицине—в форме консилиумов и т. д. Самое широкое распро­странение экспертный метод измерений получил в сфере человече­ских взаимоотношений и в области гуманитарных наук.

Разновидность экспертного метода —Органолептические изме­рения. Они основаны на использовании органов чувств человека: зрения, слуха, осязания, обоняния и вкуса. Органолептические из­мерения широко применяются в обиходе, в пищевой и парфюмер­ной промышленности, в медицине.

Комбинаторный метод измерений сочетает инструментальные и Органолептические измерения.

2.2. Измерительные шкалы

2.2.1. Шкала порядка. Простейшим видом измерения (получения опытным путем представления о каком-либо размере) яв­ляется экспериментальное сравнение его с другим размером той же меры по принципу «что больше (меньше)?» или «что лучше (хуже)?». Более подробная информация о том, насколько больше (меньше) или во сколько раз лучше (хуже) иногда даже не тре­буется. Например, масса гп\ одного из двух образцов одного и то­го же изделия (рис. 2.1) может быть больше массы та второго образца, но для решения вопроса о том, какой из них легче, по­лучаемой таким образом измерительной информации вполне до­статочно. Если изделие предназначено для использования на ле­тательных аппаратах, то качество второго образца по этому пока­зателю выше, чем первого.

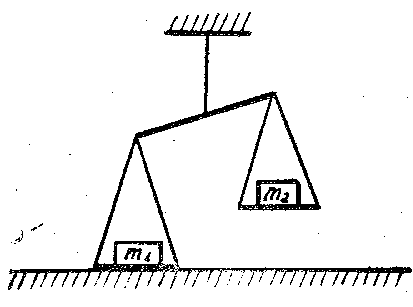
Рис. 2.1. Сравнение двух размеров одинаковой меры (массы) по шкале порядка

Подобным же образом можно визуально сравнить линейные размеры двух изделий (длину, ширину, высоту) и вынести сужде­ние о том, качество какого из изделий выше по каждому из этих показателей транспортабельности.

Можно по прибору или на глаз сравнить освещенность рабо­чего места, создаваемую разными светильниками, сделать вывод о том, качество каких светильников выше по этому эргономическо­му показателю.

Число сравниваемых между собой размеров, как в последнем примере со светильниками, может быть достаточно большим. Рас­положенные в порядке возрастания или убывания, они образуют шкалу порядка… Так, на многих конкурсах и соревнованиях мастерство исполнителей и спортсменов (или целых команд) определя­ется их местом, запятым в итоговой таблице. Последняя, таким образом, является шкалой порядка — формой представления из­мерительной информации, отражающей тот факт, что мастерство одних выше мастерства других, хотя и неизвестно, в какой степе­ни (насколько или во сколько раз). Построив людей по росту, можно, пользуясь шкалой порядка, сделать вывод о том, кто вы­ше, однако сказать, насколько выше или во сколько раз,—нельзя.

Расстановка размеров в порядке их возрастания или убывания для получения измерительной информации по шкале порядка на­зывается ранжированием.

При построении шкалы порядка (ранжированного ряда) широ­ко используется способ попарного сопоставления, когда измеряе­мые размеры сначала сравниваются между собой попарно и для каждой пары результат сравнения выражается в форме «боль­ше—меньше» или «лучше—хуже». Затем ранжирование произво­дится на основании результатов попарного сопоставления.

Пример 2.1. Результат дегустации пищевых продуктов, обозначенных номе­рами от 1 до 6, представлен в табл. 2.1, где предпочтению i-го продукта над j-м соответствует 1, а противоположному отношению—0.

Расставить продукты по качеству.

Таблица 2.1

	j
i	1		2		3		4		5		6		Итого
1		1		0		1		1		1		4
2	0			0		1		1		1		3
3	1	1		0		1		1		1		5
4	0	0		0				0		0		0
5	0	0				1				0		1
6	0	0		0		1		1				2

Решение. Ранжированный ряд (шкала порядка) имеет вид

Q4<Q5<Q6<Q2<Q1<Q3

Иногда попарное сопоставление проводят более тщательно, учитывая равноценность.

Пример 2.2. В табл. 2.2 приведены результаты попарного сопоставления ма­стерства певцов, выступавших на конкурсе вокалистов. Преимущество 1-го соли­ста над j-м обозначено 1, i-го над 1-м соответственно—1, равноценное выступление 0.

Определить итоги конкурса.

Т а б л и ц а 2.2

	j
i	1	2	3	4	5	6	Итого
1	0	1	-1	1	1	1	3
2	-1	0	-1	0	1	0	-1
3	1	1	0	1	1	1	5
4	-1	0	-1	0	1	0	-1
5	-1	-1	-1	-1	0	-1	-5
6	-1	0	-1	0	1	0	-1

Решение. Победителем конкурса стал певец выступавший третьим, второе место занял солист, выступавший первым. Третье, четвертое и пятое места по­делили между собой вокалисты, выступавшие вторым, четвертым и шестым. Последнее место досталось певцу, выступавшему пятым.

Психологами доказано, что попарное сопоставление лежит в основе любого выбора. Сравнивать размеры попарно всегда легче, чем сразу определять их место на шкале порядка.

Для облегчения измерений но шкале порядка некоторые точки на ней можно зафиксировать в качестве опорных (реперных). Зна­ния, например, оценивают но реперной шкале порядка, имеющей следующий вид: неудовлетворительно; удовлетворительно; хорошо; отлично. Точкам реперной шкалы могут быть поставлены в соответствие цифры, называемые баллами, В последнем случае шка­ла имеет вид: 2; 3; 4; 5.

Интенсивность землетрясений измеряется по двенадцатибалльной международной сейсмической шкале МSК—64 (табл. 2.3, шка­ла приведена с некоторыми сокращениями).

Таблица 2.3

Балл	Название землетрясения	Краткая характеристика
1	Незаметное	Отмечается только сейсмическими приборами
2	Очень слабое	Ощущается отдельными людьми, находящимися в состоянии полного покоя
3	Слабое	Ощущается лишь небольшой частью населения
4	Умеренное	Распознается но мелкому дребезжанию и коле­банию предметов и оконных стекол, скрипу две­рей и стен
5	Довольно сильное	Общее сотрясение зданий, колебание мебели, тре­щины оконных стекол и штукатурки, пробужде­ние спящих
6	Сильное	Ощущается всеми. Картины падают со стен, от­калываются куски штукатурки, легкое поврежде­ние зданий
7	Очень сильное	Трещины в стенах каменных домов. Антисейсми­ческие, а т;5кже деревянные постройки остаются невредимыми
8	Разрушительное	Трещины на крутых склонах и на сырой почве. Памятники сдвигаются с места или опрокиды­ваются. Дома сильно повреждаются
9	Опустошительное	Сильное повреждение и разрушение каменных до­мов
10	Уничтожающее	Крупные трещины в почве. Оползни и обвалы Разрушение каменных построек; искривление же­лезнодорожных рельсов
11	Катастрофа	Широкие трещины в земле. Многочисленные опол­зни и обвалы. Каменные дома совершенно разрушаются
12	Сильная катастро­фа	Изменения в почве достигают огромных разме­ров. Многочисленные обвалы, оползни, трещины Возникновение водопадов, подпруд на озерах. Отклонение течения рек. Ни одно сооружение не выдерживает

Твердость минералов (показатель их назначения) определяет­ся по минералогической шкале твердости (табл. 2.4).

Особенно широкое распространение измерения по шкале по­рядка получили в духовной сфере, в_ области интеллектуального труда, искусстве, гуманитарных науках, где переход к точным ко­личественным методам исследований только намечается.

По шкале порядка сравниваются между собой размеры, кото­рые сами остаются неизвестными. Результатом сравнения являет­ся ранжированный ряд. В зависимости от того, как он получен, ранжированный ряд может быть;

Таблица 2,4

Балл			Твердость
0		Меньше твердости талька
1		Равна или больше твердости талька, но меньше твердости гипса
2	Равна или больше твердости гипса, но меньше твердости известкового шпата
3		Равна или больше твердости известкового шпата но меньше твердости плавикового шпата
4		Равна или больше твердости плавикового шпата, но меньше твердости апатита
5		Равна или больше твердости апатита, но меньше твердости полевого шпата
6		Равна или больше твердости полевого шпата, но меньше твердости кварца
7		Равна или больше твердости кварца, но меньше твердости топаза
8		Равна или больше твердости топаза, но меньше твердости корунда
9		Равна или больше твердости корунда, но меньше твердости алмаза
10		Равни или больше твердости алмаза.

результатом измерений, если сравнение размеров производи­лось опытным путем;

результатом вычислений, если сравнение размеров производи­лось теоретически (расчетным методом);

смешанным ранжированным рядом, т. е- просто результатом сравнения размеров по шкале порядка, если сравнение произво­дилось и теоретически, и экспериментально.

В рассмотренных выше примерах ранжированный ряд был ре­зультатом измерений. Примером результата вычислений может служить ранжированный ряд

Sв.т. < So < Sо.т.

.где So — площадь круга, а Sв.т. и Sо.т. —площади вписанного испи­санного треугольников соответственно.

Смешанный ранжированный ряд мог бы иметь следующий вид:

S < Sв.т. < Sо.т.

где S—площадь некоторой фигуры, если бы первое неравенство было установлено экспериментально. Математической моделью теоретического сравнения между со­бой двух размеров одной меры по шкале порядка служит неравен­ство

Qi <> Qj (2.1)

а результатом сравнения —решение о том, какой размер больше другого или они равны между собой. Если все расчеты выполнены верно, то результат вычислений—решение—является правиль­ным.

В отличие от этого результат экспериментального сравнения между собой двух размеров (результат измерения) согласно ос­новному постулату метрологии является случайным, т. е. решение о том, какой размер больше другого или они равны между собой, может оказаться как правильным, так и неправильным.

Пример 2.3. У рычажных весов, показанных на рис. 2.1, длина плеч коро­мысла l1 и l2 никогда не бывает строго одинаковой. Если коромысло легкое, а длина его невелика, это различие может оставаться незамеченным.

Условие равновесия коромысла записывается следующим образом:

m₁l₁=m₂l₂

Результат измерительного эксперимента (см. рис. 2,1) означает, что

Результат измерения но шкале порядка (решение, принимаемое в предположении равноплечести весов)

m₁>m₂

может быть правильным, а может быть и неправильным, если l1>l2. При взве­шивании этих же образцов на других «равноплечих» весах он может оказаться противоположным.

Рассмотренная в примере неравноплечесть коромысла весов проявляется как мультипликативный фактор, влияющий на резуль­тат измерения по шкале порядка. В общем случае всевозможные влияния и помехи могут быть как мультипликативными, так и аддитивными. При участии в измерениях человека влияющими факторами могут оказаться утомление, рассеянность, душевные переживания, сенсорные помехи и многое другое. Все эти факто­ры делают результат измерения в той или иной степени случай­ным.

Математической моделью измерительного эксперимента в усло­виях аддитивных помех может служить выражение

Q_i+M_л <> Qj+M_п, (2.2)

в котором Qi и Qj — сравниваемые между собой размеры, а Мл и Мп — случайные изменения левой и правой части неравенства, обусловленные аддитивными влияющими факторами. При отсут­ствии общего влияющего фактора эти изменения независимы. Ре­зультат измерения по шкале порядка, т. е. принимаемое на осно­вании измерительного эксперимента решение о том, какой из раз­меров, Qi или Qj больше другого либо они равны между собой, является случайным вследствие случайности слагаемого

M=Mл-Mп (2.3)

в левой части преобразованного выражения (2.2). В иных случаях это слагаемое становится предметом самостоятельного изучения метрологами с тем, чтобы можно было повысить качество измере­ния путем внесения в результат измерительного эксперимента ад­дитивной поправки, равной приблизительно—М. При измерениях по шкале порядка такой подход не представляется возможным по следующей причине.

Измерения по шкале порядка являются самыми несовершенны­ми, наименее информативными. Они не дают ответа на вопрос о том, на сколько или во сколько раз один размер больше другого. На шкале порядка определены (т. е. могут выполняться) лишь некоторые логические операции. Например, если первый размер больше второго, а второй больше третьего, то и первый больше третьего. Или если хоть один из двух размеров больше третьего, то их сумма тоже больше третьего. Если два размера меньше тре­тьего, то их разность меньше третьего. Эти свойства шкалы поряд­ка называются свойствами транзитивности. В то же время на шка­ле порядка не определены (т. е. не могут выполняться) никакие арифметические действия. Интервалы между реперными точками неизвестны (на шкале не установлен масштаб), поэтому баллы нельзя складывать, вычитать, перемножать или делить. В принци­пе их можно заменить любыми символами (буквами или знака­ми). Измерительная информация, полученная по шкале порядка, непригодна для математической обработки (переработки). Невоз­можно и внесение в результат измерительного эксперимента поправки, ибо если ни сами сравниваемые размеры, ни разность между ними неизвестны, то останется неизвестным, изменится ли соотношение между ними после учета поправки.

Структурная схема средства измерений по шкале порядка (рис. 2.2) состоит из устройства сравнения (компаратора) и уст­ройства принятия решения. Пример компаратора (равноплечих весов без отсчётного устройства) приведен на рис. 2.1. Во многих случаях в качестве компаратора выступает человек (эксперт или экспериментатор). В таких случаях он же принимает решение.

6 Других случаях, когда компаратором является техническое уст­ройство, решение может приниматься как человеком, так и авто­матически.

Рис. 2.2. Структурная схема средства измерений по шкале порядка

Измерения по шкале порядка широко используются при конт­роле. Здесь проверяемый размер Qi сравнивается с контрольным Q2. Результатом измерения служит решение о том, годно или нет изделие по контролируемому параметру.

Особое место занимает сравнение с размером, равным нулю Оно называется обнаружением. Таково, например, обнаружение сигналов на фоне помех. Результатом обнаружения служит реше­ние о том, есть сигнал или нет. Средства измерений по шкале по­рядка, предназначенные для обнаружения, называются индикато­рами. Для обнаружения слабых сигналов они включают в себя другие устройства (кроме показанных на рис. 2.2). Последние яв­ляются оконечными устройствами индикаторов.

И результат контроля, и результат обнаружения также слу­чайны. Этим любой результат измерения всегда отличается от ре­зультата вычислений, полученного теоретическим путем. На про­цесс вычислений не оказывают влияния помехи в обычном их по­нимании, а допущенные человеком или компьютером, выполняю­щими вычисления, ошибки могут быть устранены путем много­кратных проверок. Поэтому результат вычислений не является случайным (если не являются случайными исходные данные). Пусть, например, требуется сравнить длину пути по прямой меж­ду двумя точками на плоскости с длиной любого другого пути между этими же точками. Эту задачу можно решить двумя спосо­бами: экспериментально (т. е. посредством измерений) и теорети­чески, не проводя измерений. Результат сравнения, который можно сформулировать в виде утверждения (решения): «Длина пути по прямой между двумя точками на плоскости меньше длины любого другого пути между этими точками»—в первом случае будет слу­чайным, а во втором—нет. Результат теоретического сравнения по шкале порядка двух или более размеров не является случай­ным результатом измерения.

Измеримость или неизмеримость всевозможных свойств зави­сит от воспроизводимости их мер. Некоторые меры в принципе невозможно воспроизвести, а следовательно, и сравнить между собой экспериментально (т. е. измерить) их размеры. Невоспроиз­водима, например, мера неопределенности—энтропия. Между тем можно по шкале порядка сравнить энтропию разных ситуаций и убедиться (теоретически) в том, что энтропия ситуации, ха­рактеризующейся равновероятными возможностями, больше энтро­пии ситуации с неравновероятными исходами. Этот пример вместе с предыдущим говорит о том, что теоретический метод познания также весьма эффективен и может использоваться для получения

количественной информации наряду с экспериментальным и за пределами его применимости.

2.2.2. Шкала интервалов. Более совершенной по сравнению

со шкалой порядка является шкала интервалов. На ней отклады­вается разность между размерами, которые сами Остаются по прежнему неизвестными. Принцип построения шкалы интервалов для размеров, образую­щих ранжированный ряд Q1<Q2<Q3<Q4<Q5<Q6<Q7, показан на рис. 2.3. Математической моделью теоретического сравнения между собой двух размеров одной меры здесь служит выражение

Qi-Qj=Qij (2.4)

в котором при построении шкалы интервалов с размером Q_j срав­ниваются все размеры Q_j. На рис. 2.3 в качестве Q_j выбран чет­вертый размер. Если бы в качестве Q_j был выбран размер Q₅, произошло бы смещение нуля вправо, а если бы Q₃, — влево. На­чало отсчета на шкале интервалов произвольное.

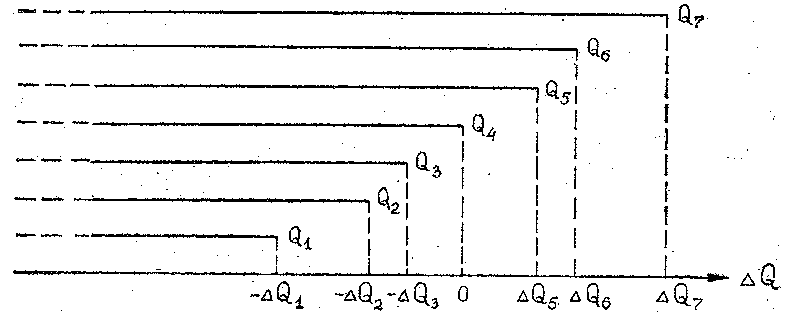
Рис. 2.3. Построение шкалы интервалов для семи размеров

Пример 2.4.

1. Насколько Токио восточнее Москвы, не зависит от того, ве­дется ли отсчет от Пулковского, Гринвичского или любого другого меридиана.

2. Насколько высота многоэтажного дома больше высоты первого этажа, hg зависит от того. ведется ли отсчет от фундамента или уровня моря.

3. Расстояние по окружности между противоположными концами диаметра равно R, независимо от начала отсчета.

На температурной шкале Цельсия (рис. 2.4) за начало отсче­та принята температура таяния льда. С ней сравниваются все дру­гие температуры. Для удобства пользования шкалой интервал между Температурой таяния Льда и температурой кипения воды разбит на 100 равных интервалов—градаций или градусов. Вся шкала Цельсия разбита на градусы как в сторону положитель­ных, так и отрицательных интервалов.

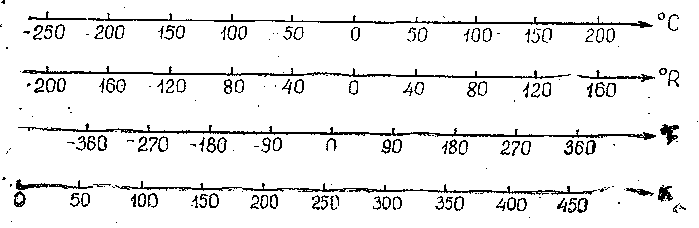
Рис. 2.4. Температурные шкалы Цельсия (°С), Реомюра (°Я), Фаренгейта (°F) и Кельвина (К)

На температурной шкале Реомюра за начало отсчета интерва­лов принята та же температура таяния льда, но интервал между этой температурой и температурой кипения воды разбит не на 100, а на 80 равных частей. Тем самым используется другая гра­дация интервалов температуры: градус Реомюра больше градуса Цельсия.

На температурной шкале Фаренгейта тот же интервал разбит на 180 градусов. Следовательно, градус Фаренгейта меньше гра­дуса Цельсия. Кроме того, начало отсчета интервалов на шкале Фаренгейта сдвинуто на 32° в сторону низких температур.

Деление шкалы интервалов на равные части — градации — устанавливает на ней масштаб и позволяет выразить результат измерения в числовой мере. При наличии масштаба измерение по шкале интервалов сводится к подсчету числа градаций, уклады­вающихся в интервале Qij. Градация, таким образом, выступает в качестве единицы измерения.

Особым случаем является сравнение Qi с Qj=0. В отличие от измерений по шкале порядка, где подобное сравнение производит­ся с целью обнаружения Q;, на шкале интервалов такое сравнение позволяет измерить Qi (, ибо, как это следует из формулы (2.4), измерение интервала Qi при Qj =0 тождественно измерению са­мого размера Qi (. Подробно этот случай рассматривается в п. 2.2.3).

Примером шкалы интервалов, построенной при Qj =0 (она на­зывается шкалой отношений—cм.п. 2.3), может служить темпе­ратурная шкала Кельвина, приведенная на рис. 2.4. На ней за на­чало отсчета принят абсолютный ноль температуры, при котором прекращается тепловое движение молекул. Более низкой темпера­тура быть не может. Второй реперной точкой служит температура таяния льда. По шкале Цельсия интервал между этими реперами равен 273,16°С. Поэтому на шкале Кельвина он разделен на равные части, составляющие 1/273,16 интервала. Каждая такая часть называется Кельвином и равна градусу Цельсия, что значительно облегчает переход от одной шкалы к другой.

На шкале интервалов определены такие математические дейст­вия, как сложение и вычитание. Интервалы с учетом знака можно складывать друг с другом и вычитать друг из друга. Благодаря этому можно определить, на сколько один размер больше или мень­ше другого. Так, на рис. 2.3

Q7-Q5=Q7—Q5;

Q5—Q2=Q5— (—Q2) = Q5 + Q2 (2.5)

Q3—Q1= —Q3(—Q1) = Q1—Оз.

Аддитивные операции' по формулам (2.5) выполняются с раз­мерами интервалов, полученными по формуле (2.4), т. е. по не­отградуированной шкале (см. рис. 2.3). Если шкала отградуиро­вана (см. рис. 2.4),то размеры интервалов выражены в опреде­ленных еди-ницах измерения. Следовательно, по отградуированной шкале определяются значения интервалов по формуле

Qi—Qj=Qij (2.6)

В этом случае

Q7—Q5 = Q7—Q5;

Q5—Q2 = Q5—(—Q2) = Q5 + Q2; (2.7)

Q3—Q1 = —Q3—(—Q1) = Q1—Q3.

Формулы (2.7) используются при переработке результатов из­мерений по шкале интервалов, при разного рода теоретических вычислениях, в том числе при сравнении показателей качества по шкале интервалов расчетным методом, не относящимся к измере­ниям.

На рис. 2.5 показана трансформация шкалы интервалов для автотуриста, следующего через Москву в Ленинград. В первом случае (рис. 2.5, а) он находится в Москве, во втором (рис;' 2.5,6) —в Твери, в третьем (рис. 2,5, в) —в Новгороде. Откуда бы

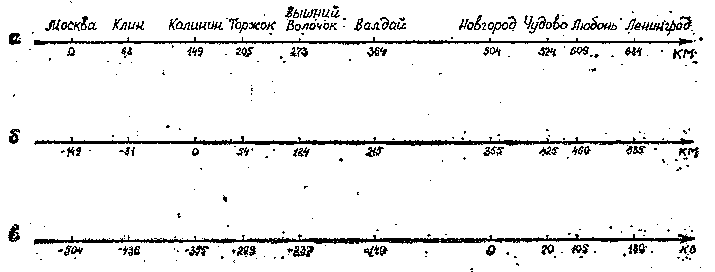
Рис. 2-5. Пример шкалы интервалов

да он ни ехал, расстояние от Торжка до Валдая (разности пути до Валдая и до Торжка) равна 159 км. В первом случае это раз­ность пути от Москвы до Валдая и от Москвы до Торжка. Во вто­ром случае—разность расстояний между Тверью—Валдаем и Тверью—Торжком. В третьем случае—между Новгородом—Вал­даем и Новгородом—Торжком. Легко можно проверить справед­ливость и других аддитивных операций, но если задаться вопро­сом, во сколько раз Ленинград дальше Чудова, то окажется, что в первом случае в 1,19, во втором—в 1,26, а в третьем—в 2,57 раза. Определенного ответа на вопрос, таким образом, нет.

Ввиду неопределенности начала отсчета мультипликативные операции (умножение и деление) на шкале интервалов не опреде­лены. Соответственно по шкале интервалов нельзя определить, во сколько раз один размер больше или меньше другого.

Пример 2.5. Время измеряется по шкале интервалов. Единицами измерения (градациями) являются год, квартал, месяц, неделя, сутки, час, минута, секунда и т. д. Но начало отсчета времени (как и пути) может быть выбрано произ­вольно. При любом начале отсчета коренной перелом в ходе второй мировой войны произошел под Сталинградом спустя 700 лет после разгрома Александ­ром Невским немецких рыцарей Ливонского ордена на льду Чудского озера. Если же поставить вопрос о том, во сколько раз позже наступило это событие, то окажется, что по юлианскому календарю, где время отсчитывается «от сотво­рения мира», в 7448/6748  1,1 раза; по иудейскому, ведущему отсчет времени «от сотворения Адама», в 5б38/4938  1,14 раза; по григорианскому стилю, в котором отсчет времени начинается «с рождества Христова», в 1942/1242 1,56 раза, а по магометанскому летоисчислению, начинающемуся с момента бегства Магомета из Мекки в священный город Медину, где была основана первая му­сульманская община, в 1320/620  2.13 раза. Однозначного ответа на поставлен­ный вопрос не существует.

Структурная схема средства измерений по градуированной шка­ле интервалов представлена на рис. 2.6.

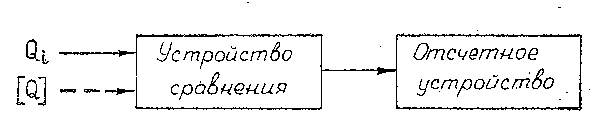
Рис. 2-6. Структурная схема средства измерений по, шкале интервалов.

В устройстве сравнения осуществляется операция (2.4). Так как размер Qj, с которым производится сравнение, остается одним И тем же при разных Qj, подавать его всякий раз на вход сред­ства измерений нет необходимости. Информация о нем заклады­вается в устройство сравнения один раз и хранится в нем посто­янно. Такой информацией может быть, например, высота ртутного столба в термометре при температуре таяния льда.

Главным элементом отсчётного устройства, в котором осущест­вляется преобразование

QijQij (2.8)

является градуированная шкала. Для того чтобы по ней подсчи­тывалось, сколько единиц измерения [Q] укладывается в интер­вале Qij, в отсчетное устройство должна быть заложена инфор­мация о размере единицы. Так как размер единицы сам является интервалом, то в отсчетное устройство можно заложить информа­цию об интервале, известная часть которого — размер единицы. Зафиксировать, например, насколько увеличивается высота, ртут­ного столба термометра при переходе от температуры таяния льда к температуре кипения воды. Тогда на равномерной темпе­ратурной шкале информацией о градусе Цельсия будет 1/100 этого интервала, информацией о градусе Реомюра — 1/80 его часть. Эти градации называются делениями шкалы, а процедура пере­дачи средству измерений информации о размере единицы (опре­деление цены деления шкалы) называется градуировкой.

Реальные измерения отличаются от их теоретической модели, тем, что происходят в условиях влияния множества факторов, точный учет совместного воздействия которых невозможен. Влия­ющие факторы проявляются при каждой измерительной операции. Измерение по градуированной шкале интервалов в соответствии с его математической моделью (2.6) включает две такие операции: первая (см. уравнение 2.4) выполняется устройством сравнения, вторая (см. преобразование 2.8)—отсчетным устройством. Устройством сравнения могут быть, например/рычажные весы, подобные показанным на рис. 2.1, а отсчетным устройством— шкала со стрелочным указателем, по которой определяется зна­чение

m = m1 – m2

Факторы, влияющие на первую операцию, рассмотрены в разд. 2.2. Ограничиваясь для простоты опять-таки только адди­тивными влияниями и учитывая совместное действие всех факто­ров случайным слагаемым M, после операции сравнения (2.4) в реальных условиях получим

m1-m2 =m-M,

где разность коррелированных слагаемых в правой части уравне­ния не является случайной. Согласно (2.8), правая часть этого уравнения должна быть преобразована отсчетным устройством следующим образом: m-M m-M. Однако пpeoбpaзoвaниe также выполняется в условиях разных воздействий. Учитывая и их суммарное влияние аддиативным случайным слагаемым Н, получим

m – M m – M - H

. Здесь

X = m – M – H (2.10)

—показание средства измерений. Его числовое значение х на градуированной шкале называется отсчетом по шкале интервалов.

Определенное выражением (2.10) показание, возможно, зани­жено по сравнению с интересующим нас значением Am и кроме того является случайным. В ходе специальных метрологических исследований иногда удается получить представление о законе распределения вероятности каждого из двух последних слагаемых в правой части уравнения (2.10) или оценить их средние значения. Тогда в показание средства измерений вносится поправка

__ __

M + H

Так как она не является случайной, то после ее внесения за­кон распределения вероятности показания Х смещается по оси абсцисс на . Результат измерения

m = X +  

получается после внесения в показание средства измерений по­дправки.

Поправка может быть положительной (когда, например, часы отстают) и отрицательной (когда часы спешат). В отдельных слу­чаях она может оказаться равной нулю либо может быть принята равной нулю и не вноситься. В общем случае внесение в показа­ние средства измерений Х поправка  обеспечивает правильность результата измерения

AQ-JC+0. (2.11)

Результат измерения, согласно выражению (2.11) и основно­му постулату метрологии, является случайным. Вследствие этого

на шкале интервалов результаты измерений имеют вид, показан­ный на рис. 2.7,

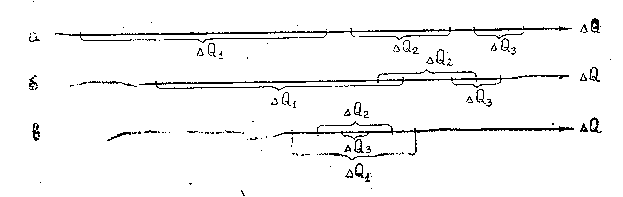
Рис, 2.7. Результаты измерений на шкале интервалов;

а — в примере 2.6, б — в примере 2.7, в — в примере 2.8

Пример 2.6. При испытаниях на надежность измеряется интервал времени Q между началом эксплуатации (включением аппаратуры) и первым отка­зом. Этот показатель качества называется временем безотказной работы. Пред­положим, что время безотказной работы каждого из трех изделий измеряется отдельным средством измерений, причем закон распределения вероятности показаний у них нормальный со стандартным отклонением соответственно: S1 = 2,5с; S2 = 0,5с; Sз= 0,25 с.

Принимая поправки к показаниям средств измерений равными нулю, определить с вероятностью 0,95 время безотказной работы каждого из трех изделий.

Решение. Как следует из графика, приведенного на рис. 2.8, время безотказной работы 1-го изделия не может отличаться от показания соответствующего средства измерений Хi больше чем на 2 Si. Поэтому

Q1 = X1±2S1 = (X1±5) с,

Q2 = Х2±2S2 = (X2±1) с,

Q3 = Хз ±2S3 = (Хз±0,5) с.

Иллюстрацией этого служит рис. 2.7, а.

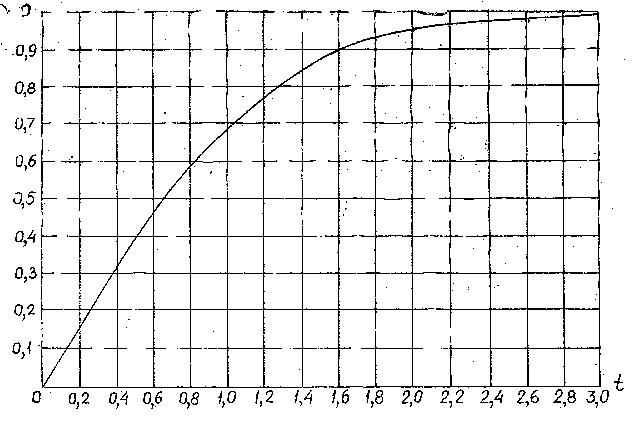
Рис. 2,8. Вероятность попадания отдельного значения случайного числа, подчиняющегося нормальному закону распределения вероят­ности, в окрестность среднего значения.

Пример 2.7. При климатических испытаниях изделий интервал Q между температурой воздуха в камере и температурой тройной точки воды измеряется по мере нагрева равными термометрами с неравными значениями отсчета. На рис. 2.7. б показан пример измерения температуры в камере тремя термо­метрами.

Пример 2.8. При измерении разности потенциалов AQ вольтметрами разных классов точности их показания совпали. Как должен интерпретироваться этот случаи?

Решение. Информация о разности потенциалов, полученная каждым из трех вольтметров, представлена на рис. 2.7, в.