3.6. Дифракция Фраунгофера на дифракционной решетке

О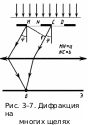 дномерная дифракционная решетка — система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ши­рине непрозрачными промежутками. На рис. 3-7 для наглядности показаны только две соседние щели MN и CD. Ширина щели а, а ширина не­прозрачных участков между щелями b, величина d = a + b называется постоянной дифракционной решетки (периодом). Щели находятся друг от друга на одинаковых расстояниях поэтому разности хода лучей, идущих от соседних щелей, будут для данного направления  одина­ковы в пределах всей дифракционной решетки:

. (3-12)

В точке В на экране в фокальной плоскости линзы соберутся лучи, которые до линзы были параллельны между собой и распространялись под углом  к направлению падающей волны.

Очевидно, что в тех направлениях, в которых ни одна из щелей не распро­страняет свет, он не будет распростра­няться и при двух щелях, т. е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяе­мых условием (3.10):

(3-13)

Кроме того, вследствие взаимной интерфе­ренции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т. е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут на­блюдаться в тех направлениях, которым соответствует разность хода лучей /2, З/2, ..., посылаемых, например, от край­них левых точек М и С обеих щелей. Таким образом, с учетом (3-12) условие дополнительных минимумов:

Для того, чтобы в точке В наблюдался интерференционный максимум, разность хода Δ между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн (четному числу полуволн):

, (3-14)

т.е. выражение (3-14) задает условие главных максимумов.

Таким образом, полная дифракцион­ная картина для двух щелей определяется из условия:

главные минимумы 

дополнительные минимумы 

главные максимумы 

т. е. между двумя главными максимумами располагается один дополнительный минимум. Аналогично можно показать, что между каждыми двумя главными макси­мумами при трех щелях располагается два дополнительных минимума, при четырех щелях — три и т. д.

Если дифракционная решетка состоит из N щелей, то усло-вием главных миниму­мов является условие (3-13), условием главных максимумов - условие (3-14), а условием дополнительных минимумов

(3-15)

где m^* может принимать все целочислен­ные значения, кроме 0, N, 2N, ..., т. е. кро­ме тех, при которых условие (3-15) пере­ходит в (3-14). Следовательно, в случае N щелей между двумя главными максиму­мами располагается N—1 дополнитель­ных минимумов, разделенных вторичными максимумами, создающими

весьма сла­бый фон.

Чем больше щелей N, тем большее количество световой энергии пройдет че­рез решетку, тем больше минимумов обра­зуется между соседними главными макси­мумами, тем, следовательно, более интен­сивными и более острыми будут максиму­мы.

Н а рис. 3-8 качественно представлено распределение резуль-тирующей интенсивности в дифракционной решетке.

При пропускании через решетку белого света все максимумы, кроме цен­трального (m = 0), разложатся в спектр, фиолетовая область которого будет обра­щена к центру дифракционной картины, красная — наружу. Это следует из формулы (3-14) в которой угол отклонения m – го максимума   . Это используется для иссле­дования спектрального состава света (оп­ределения длин волн и интенсивностей всех монохроматических компонентов), т.е. дифракционная решетка может быть использована как спектральный прибор. Распределение энергии по спектрам разных порядков показывает, что значительная часть энергии сосредоточе­на в спектре нулевого порядка (рис. 3-6, б ) и по мере перехода к высшим порядкам энергия быстро убывает. Спектральные приборы, снабженные таки­ми дифракционными решетками, были бы мало светосильны. Устранить данный недостаток предложил английский физик Дж. У. Рэлей, а осуществил это предложение американский физик Р.У.Вуд. Было предложено ввести дополнительную разность хода в пре­делах каждого штриха решетки. С этой целью решетку гравируют так, что каждая борозда имеет определенный профиль, благодаря чему при отражении (или при прохождении) возникает добавочная раз­ность хода от одного края борозды до другого (рис. 3-9). Подбирая профиль борозды, удается сконцентрировать энергию в спектре того или иного порядка, ослабляя остальные, в том числе и самый яркий спектр нулевого порядка. Решетки подобного типа позволили сделать дифракционные спектрографы инструментом, превос-х одящим по све­тосиле обычные призматические спектрографы.

Решетки, изображенные на рис. 3-9, представляют собой фазовые решетки, отдельные элементы которых отличаются не различием в отражающей или пропускающей способности, влияю­щей на амплитуду волны, а своей способностью изменять фазу волны. В этом случае изменение фазы происходит вследствие геометриче­ской формы пластинки, отражающей или пропускающей волну.

М ож­но воздействовать на фазу волны за счет различия в показателе преломления пропускающего слоя при его неизменной толщине; тако­го рода фазовые решетки удается создавать, вызывая в прозрачном теле ультраакустическую волну.

Фазовая отражательная решетка, использующая различие в изменении фазы при полном вну­треннем отражении от се­ребра и стекла показана на рис. 3-10. Для этого на гипотенузную грань стеклянной 90-градусной поворотной призмы были нанесены полоски серебра, которые разделены полосками стекла без серебрения. При падении света со стороны стекла интен­сивность света, отраженного от тех или иных полосок, практичес­ки одинакова (за счет полного внутреннего отражения), но возникает разли­чие в фазах, которое и приводит к обра­зованию дифракционной картины. Возможны, конечно, решетки амплитудно-фазовые, т.е. воздей­ствующие одновременно как на фазу, так и на ам­плитуду.