9

ЛАБОРАТОРНАЯ PAБОТА № 3

Стабилизация релейных систем. Скользящие режимы. Автоколебания.

1.

1. Цель проведения лабораторной работы

- исследование релейной системы регулирования 2-го порядка методом фазовой плоскости.

2. Задачи исследования

- закрепить теоретический материал по разделу «Нелинейные системы управления», изучить методику построения фазовых траекторий линейных систем;

- усвоить понятия фазовой плоскости, автоколебаний и их устойчивости;

- знать свойства скользящего режима и условия его возникновения, сущность метода точечных преобразований.

3. Краткие теоретические сведения

В системе с идеальным реле наблюдаются незатухающие колебания, амплитуда которых может принимать значения, зависящие от начальных условий. В случае с реле с гистерезисом колебания вообще расходящиеся.

Причиной этого является задержка переключения реле (пространственное запаздывание), благодаря чему регулируемая величина существенно отклоняется от заданного значения.

Улучшения качества можно достичь, если охватить РЭ обратной связью по скорости (рис. 1).

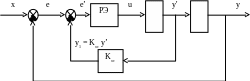
Рисунок 1 – Релейная система с обратной связью по скорости

В этом случае на вход РЭ вместе с сигналом ошибки е поступает сигнал у₁, пропорциональный скорости изменения регулируемой величины.

Результирующий сигнал е₁, поступающий на вход РЭ, определяется формулой

. (1)

Учитывая, что х = const, а , уравнение (1) запишем следующим образом:

(2)

Переходя к фазовым координатам, получим

(3)

Переключения реле определяются теперь сигналом е₁. Но поскольку выход реле u(t) по-прежнему может принимать лишь значения b, уравнения фазовых траекторий остаются неизменными, изменяется лишь линия переключения. Проведем анализ фазовых траекторий скорректированной системы для двух типов реле.

3.1. Идеальное реле.

В этом случае (рис. 1) при е₁ > 0 значение u = b положительно и движение происходит по правой полуплоскости. Переключение реле происходит, когда входной сигнал е₁ равен нулю:

(4)

Прямая (4) определяет на фазовой плоскости (рис. 2) линию переключения и делит плоскость на две области.

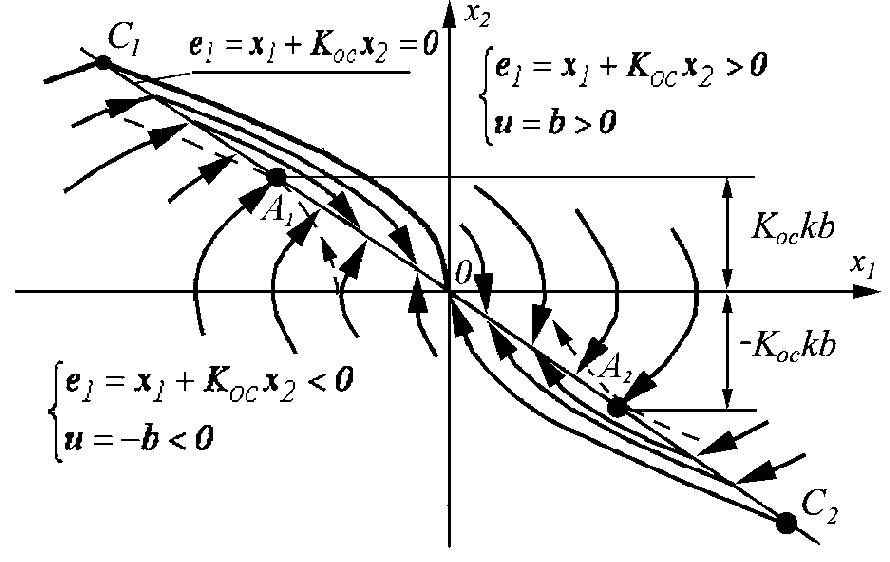
Рисунок 2 – Фазовый портрет системы

Смысл рассматриваемой коррекции заключается в том, что переключение реле происходит раньше, чем изменяется знак ошибки. Таким образом создается опережающий эффект и фазовые траектории сходятся к началу координат. Характерной особенностью фазового портрета является наличие так называемого скользящего режима. Скользящему режиму на рис. 2 соответствует отрезок А₁А₂.

Вне отрезка скольжения фазовые траектории правой и левой полуплоскости направлены «согласно» друг другу, и переключения реле происходят как обычно. На отрезке скольжения фазовые траектории правой и левой полуплоскости направлены навстречу друг другу. Изображающая точка не может уйти с линии переключения, но и не может на нем остаться, так как ее скорость за исключением начала координат не равна нулю. Изображающая точка вынуждена двигаться вдоль линии переключения к центру. Причем переключения реле происходят с бесконечно большой частотой. Движение по линии переключения подчиняется уравнению

(5)

или, возвращаясь к старым координатам,

. (6)

Решением дифференциального уравнения (6), как известно, является экспонента

. (7)

Таким образом, в режиме скольжения переходный процесс протекает по экспоненте и, что весьма существенно, не зависит от свойств объекта. В общем случае переходная кривая, совершив конечное число колебаний, стремится к своему установившемуся значению по экспоненте.

Граничные точки отрезка скольжения А₁А₂ (рис. 2) определяются как точки касания линии переключения соответствующих траекторий (показаны на рис. 2 пунктиром). Тангенс угла наклона линии переключения равен –1/K_oc. Поэтому условие касания фазовой траектории линии переключения записывается следующим образом:

, (8)

где производная находится из уравнений

для точек А₁ и А₂ соответственно.

Дифференцируя уравнение по х₁ и считая х₂ функцией х₁, получим для точки А₁

. (9)

Подставляя теперь значение из (8) в (9), найдем координату точки А₁

. (10)

Координаты точки А₂ отличаются лишь знаком (рис. 2).

Таким образом, от параметров объекта зависит только длина отрезка скольжения.

3.2 Реле с гистерезисом.

Проведем анализ фазовых траекторий системы при наличии обратной связи (рис. 3). Переключения реле (рис 3,а) определяются теперь условиями

( 11)

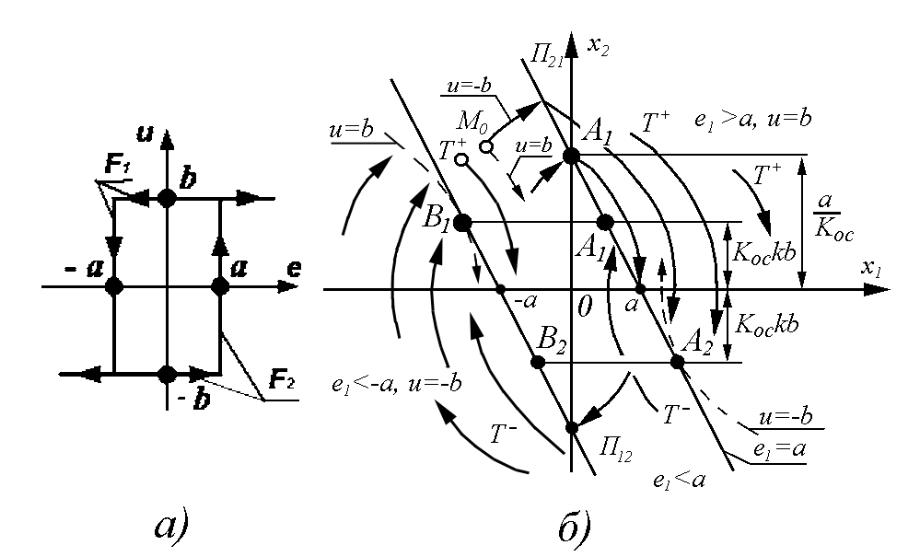
Рисунок 3 – Условия переключения фазовых траекторий

Условия (11) являются необходимыми и задают на фазовой плоскости пару прямых (рис. 3,б). Движение изображающей точки происходит по траекториям Т⁺ правой полуплоскости; при e₁ < -а значение u = -b, и движение происходит в левой полуплоскости. В области |e₁| < а движение изображающей точки в зависимости от состояния реле (u = b или u = -b) может происходить в любой полуплоскости.

На прямой e₁ = a может происходить только переключение П₂₁ – переход u(t) (рис. 3,а) с ветви F₂ на ветвь F₁, то есть переход изображающей точки со второго листана первый. Выделим множество точек прямой е₁ = a, образующих линию переключения П₂₁. В области e₁ > а проходят траектории Т⁺ правой полуплоскости (рис.3). Траектории Т^- левой полуплоскости могут подходить е₁ = а только слева из области |e₁| < а. Это возможно только в тех точках прямой е₁ = а, где угол ее наклона больше угла наклона касательной к фазовой траектории. Предельной здесь является точка А₂ (рис. 3,б), где одна из траекторий семейства Т^- касается прямой е₁ = а. Точки прямой е₁ = , лежащие выше точки А₂, и образуют линию переключения П₂₁.

Аналогично на прямой е₁ = -а возможны только переключения П₁₂ – переход u(t) (рис. 3,а) с ветви F₁ на ветвь F₂, а изображающая точка переходит с правой полуплоскости на левую (рис. 3,б). Траектории Т⁺ могут достичь прямой е₁ = -а только из области |e₁| < а. Все точки прямой е₁ = -а, лежащие ниже точки В₁, в которой одна из траекторий семейства Т⁺ касается прямой, образуют линию переключения П₁₂. (рис. 3,б).

Найдем координаты точек касания А₂ и В₁. Тангенс угла наклона прямых (11) равен –1/К_ос. В разделе 3.1 при исследовании системы с идеальным реле было показано, что координаты точек касания прямой с таким наклоном и фазовых траекторий равны . Учитывая этот результат, уравнения линий переключения П₁₂ и П₂₁ можно записать следующим образом:

П₁₂:

П₂₁: (12)

В исследуемой системе существует предельный цикл – замкнутая изолированная траектория, проходящая через точки Д₁ и Д₂ (рис. 4).

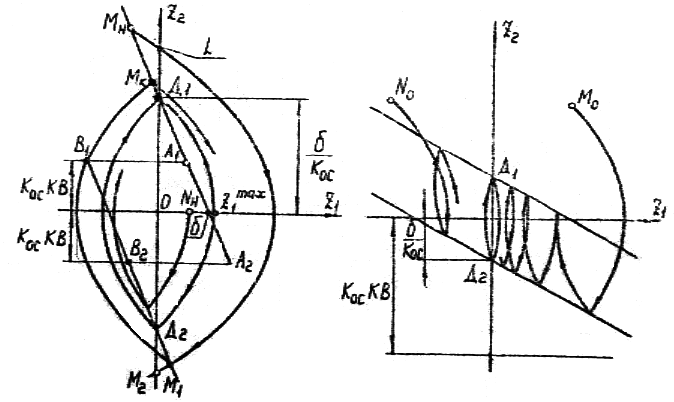
Рисунок 4 – Предельные циклы в релейной системе

Действительно, фазовая траектория, исходящая из точки Д₁, в силу симметрии относительной оси х₁ обязательно пройдет через точку Д₂ и наоборот.

Предельному циклу соответствуют периодические незатухающие колебания – автоколебания. Характер автоколебаний (амплитуда, поведение траекторий в близи предельного цикла) существенно зависит от степени обратной связи (рис. 4). Следует отличать два случая, представленные на рис. 4:

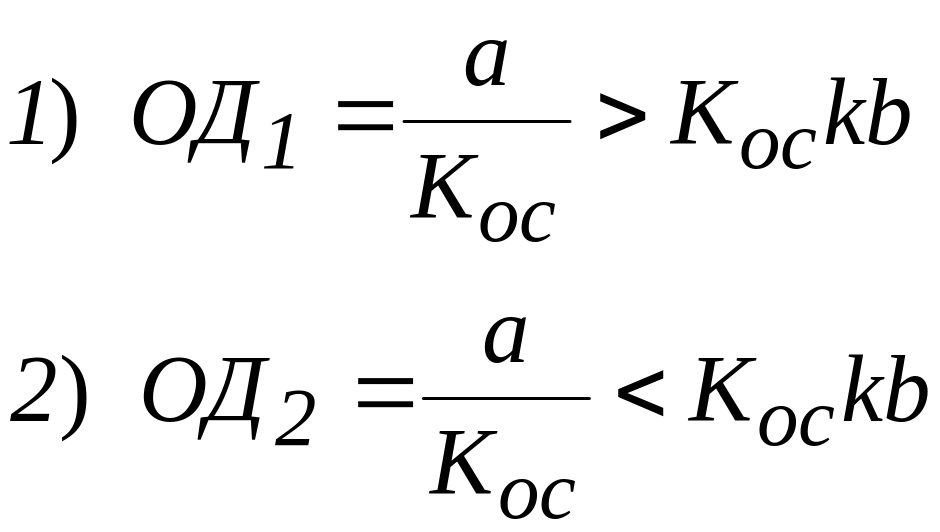(13)

В первом случае (рис. 4,а) траектория предельного цикла всегда пересекает линии переключения – имеют место «нормальные переключения». Во втором (рис. 4,б) – предельная траектория целиком лежит внутри области между линиями переключения, амплитуда автоколебаний х₁^max < а и про цесс установления автоколебаний носит своеобразный характер, напоминающий в какой-то мере скользящий режим. Таким образом, при соответствующем выборе K_oc амплитуда автоколебаний становится меньше зоны нечувствительности, качество регулирования повышается. Объясняетcя это тем, что сигнал е₁ на выходе реле есть сумма е₁ = Z₁ + K_oc х₂. Амплитуда e₁^max, естественно, не может быть меньше , но каждое из слагаемых, в частности х₁, может быть достаточно мало, в особенности при больших K_oc, как это показано на рис. 4,б.

Амплитуда автоколебаний х₁^max

(14)

Из полученной формулы видно, что амплитуда автоколебаний уменьшается с ростом K_oс.

Теперь из (14) легко получить условия, при которых х₁^max  а:

. (15)

Предельный цикл единственный и соответствует устойчивым автоколебаниям. Поскольку выбор начальной точки произволен, то сходимость доказана для всех траекторий, начинающихся вне предельного цикла.