9

Лабораторная paбота № 1 Исследование релейных систем на фазовой плоскости

1. Введение

Релейные системы получили широкое распространение в практике автоматического регулирования. Достоинством релейных систем является простота конструкции, надежность, простота обслуживания и настройки. Релейные системы представляют собой особый класс нелинейных АСР.

В отличие от непрерывных в релейных системах регулирующее воздействие изменяется скачкообразно всякий раз, когда управляющий сигнал реле (чаще всего это ошибка регулирования) проходит через некоторые фиксированные (пороговые) значения, например, через нуль.

Релейные системы, как правило, обладают высоким быстродействием вследствие того, что управляющее воздействие в них изменяется практически мгновенно, а на исполнительное устройство действует кусочно-постоянный сигнал максимальной амплитуды. В то же время в релейных системах часто возникают автоколебания, что во многих случаях является недостатком. В настоящей работе исследуется релейная система с четырьмя различными законами управления.

2. Цель проведения лабораторной работы

- исследование релейной системы регулирования 2-го порядка методом фазовой плоскости.

3. Задачи исследования

- закрепить теоретический материал по разделу «Нелинейные системы управления», изучить методику построения фазовых траекторий линейных систем;

- усвоить понятия фазовой плоскости, автоколебаний и их устойчивости;

- знать свойства скользящего режима и условия его возникновения, сущность метода точечных преобразований.

3. Краткие теоретические сведения

3. 1. Анализ релейных систем на фазовой плоскости.

Фазовая плоскость – это плоскость двух независимых переменных (х₁ и х₂), в которых можно однозначно задавать движение нелинейной системы. Часто в качестве этих переменных принимают какой-либо параметр системы и скорость его изменения.

Фазовая плоскость является весьма эффективным средством для исследования нелинейных систем второго порядка. На фазовой плоскости можно производить анализ движений нелинейной системы, исследовать устойчивость и качество регулирования и, наконец, осуществлять синтез нелинейных систем.

Большой класс нелинейных систем может быть представлен как последовательное соединение нелинейного элемента (в данном случае РЭ) и линейной части (ЛЧ).

Рисунок 1 – Структурная схема релейной системы

Геометрическое место точек на фазовой плоскости, соответствующих последовательным состояниям системы, называется фазовой траекторией.

Полная совокупность фазовых траекторий, соответствующая всем возможным начальным условиям, называется фазовым портретом.

3.2. Уравнения фазовых траекторий релейной системы

Ограничимся линейной частью с передаточной функцией вида:

. 1)

Структурная схема такой системы приведена на рис. 2.

Рисунок 2 – Структурная схема релейной АСР

Найдем уравнения фазовых траекторий системы. Для этого запишем уравнения элементов системы:

- уравнение ЛЧ;

u = Ф₁(е) - уравнение РЭ; (2)

е = х – у - уравнение замыкания.

Вид функции u = Ф₁(е) зависит от типа РЭ. Будем считать, что входной сигнал x(t) может принимать только постоянные значения, т.е. x(t)=x₀=const.

Тогда из уравнения е = х - у следует, что

(3)

Подставляя выражение из (4) и u = Ф₁(е) в уравнение ЛЧ (2), получим дифференциальное уравнение замкнутой системы относительно ошибки регулирования

, (4)

где Ф(е) = k Ф₁(е).

Нелинейная функция может принимать три значения:

, (5)

а ее конкретный вид зависит от типа реле (рис.3).

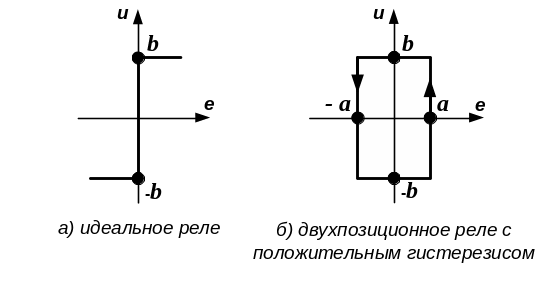
Рисунок 3 - Характеристики релейных элементов

Введем в рассмотрение фазовые координаты х₁ и х₂:

. (6)

Таким образом, – ошибка регулирования, а – скорость ее изменения.

Подставляя соотношение (6) в (4) и учитывая, что , получим

(7)

Система уравнений (7) эквивалентна уравнению (4). Поделив теперь второе уравнение (7) на первое и исключив так им образом время, получим дифференциальное уравнение фазовых траекторий системы:

(8)

Поскольку функция Ф принимает лишь постоянные значения, то переменные в (8) легко разделяются:

(9)

Интегрируя последнее выражение, получим

. (10)

Постоянная С₁ зависит от начальных условий. Подставляя теперь в уравнение (10) последовательно значения и преобразовав, получим уравнение фазовой траекторий:

область I (11)

область III (12)

область II (13)

Уравнения (11) и (12) определяют семейства парабол, отличающихся лишь направлением ветвей.

Соответствующие фазовые траектории показаны на рис. 4.

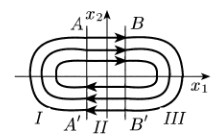
Рисунок 4 – Фазовые траектории листов релейной АСР

По уравнениям (11) – (13) легко построить фазовый портрет релейной системы для различных РЭ.