Вопросы к работе

1. Что такое водородный показатель? Чему равен рН чистой воды при 25°

2. Стеклянный электрод. Устройство, принцип действия, применение.

3. Диссоциация, степень диссоциации. Закон разведения Оствальда.

4. Концентрация и активность, разница между ними. Когда эти понятия тождественны.

5. Коэффициент активности, его связь с концентрацией.

6. Выведите зависимость рН от К_дис. для уксусной кислоты.

Литература.

1. Зимон А.Д., Зарубин Д.П., Лукина И.Г., Евтушенко А.М., Павлов А.Н., Аксёнов В.Н. Физическая химия. Лабораторный практикум. М.: МГТА, 2003 (лаб. работа 3).

2. Зимон А.Д., Лещенко Н.Ф. Физическая химия. М.: Высшая школа, 2000.

РАБОТА № 4

ИЗМЕРЕНИЕ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ ГАЛЬВАНИЧЕСКОГО ЭЛЕМЕНТА.

Цель работы: Приготовление гальванического элемента, измерение его э.д.с. Вычисление э.д.с. элемента при заданных концентрациях солей. Сравнение полученных результатов с вычисленными значениями э.д.с.

Краткое теоретическое введение

Гальванический элемент представляет собой устройство, состоящее из проводников первого (металлы) и второго (электролиты) рода, находящихся в контакте друг с другом. На границах раздела различных проводников, например, металл-раствор, создаются скачки потенциалов, в результате чего в гальваническом элементе возникает электродвижущая сила. При работе гальванического элемента химическая энергия реакции, протекающая нем, переходит в электрическую энергию. Если химическая реакция протекает в элементе обратимо, то и сама цепь будет обратимой, а при этом работа - максимальной.

Примером обратимого гальванического элемента является элемент Якоби-Даниэля, состоящий из медного и цинкового электродов, которые погружены соответственно в растворы CuSO₄ и ZnSO₄. Элемент Якоби-Даниэля может быть записан схематически:

(-)Zn|ZnSO₄||CuSO₄|Cu(+),

г де вертикальная черта означает поверхность раздела фаз металл-раствор, а две вертикальные черты - раствор-раствор.

В результате работы данного элемента на цинковой электроде будут образовываться и переходить в раствор ионы Zn²⁺; Zn®Zn²⁺+2e, а на медном электроде будут разряжаться ионы Cu²⁺ и осаждаться металлическая медь.

Cu²⁺ + 2e® Cu

Во внешней цепи электроны будут переходить от цинкового электрода к медному и будет возникать электродвижущая сила. Суммарный химический процесс выражается уравнением

Cu²⁺ + Zn ® Cu⁰ +Zn²⁺

На границе раздела фаз ZnSO₄||CuSO₄ возникает диффузионный потенциал, который стремятся свести к минимуму из-за невозможности его измерения при помощи солевого мостика, обычно состоящего из насыщенного раствора электролита, у которого подвижности катиона и аниона одинаковы (КCl, NH₄NO₃). Элемент Якоби-Даниэля (рис. 4.1.) с применением солевого мостика можно изобразить следующим образом:

(-)Zn|ZnSO₄|KCl|CuSO₄|Cu(+),

Потенциал металла, погруженного в раствор соли этого металла, определяется уравнением Нернста:

(4.1)

где φ⁰ - стандартный потенциал электрода,

R - универсальная газовая постоянная,

n - валентность катиона,

a - активность ионов металла,

F - постоянная Фарадея.

Значения стандартных потенциалов определяют по отношению к водородному электроду, стандартный потенциал которого условно принят за ноль. Значения стандартных потенциалов приводятся в справочниках. Итак, для медного электрода имеем:

, (4.2)

а для цинкового электрода:

, (4.3)

э.д.с. цепи равна разности потенциалов медного и цинкового электродов:

, (4.5)

где а - стандартные значения потенциалов медного и цинкового электрода соответственно.

Э.д.с. гальванического элемента характеризует максимальную полезную работу, которая может быть произведена системой при протекании в ней данной химической реакции:

, (4.6)

где W ^/_m - максимально полезная работа,

DG - изменение энергии Гиббса,

n - число электронов, принимающих участие в электрохимической реакции,

F - постоянная Фарадея,

E - э.д.с. гальванического элемента.

Стандартная э.д.с. гальванического элемента вычисляется по формуле:

, (4.7)

где К_а - константа равновесия реакции.

Большое значение константы равновесия показывает, что в рассматриваемой реакции равновесие практически целиком смещено в сторону прямой реакции.

Активностью называется термодинамическая величина, позволяющая представить в удобной для практического использования форме концентрационную зависимость химических потенциалов реального раствора. С помощью этой величины можно применять к реальному раствору термодинамические соотношения, относящиеся к идеальному раствору, если заменить в них концентрации активностями.

Активность связана с концентрацией раствора зависимостью:

, (4.8)

где - коэффициент активности.

Коэффициент активности зависит от ионной силы и других свойств раствора. Ионная сила раствора определяется выражением:

, (4.9)

где c_i – молярная концентрация иона,

z_i – заряд иона.

Суммирование производится по всем типам ионов, присутствующих в растворе.

Коэффициенты активности индивидуальных ионов в разбавленных растворах в теории межмолекулярных взаимодействий вычисляются по уравнению Дебая-Хюккеля:

, (4.10)

где А = 0,5092 (дм³/моль)^1/2, Ва^/ = 1 (дм³/моль)^1/2.

Электродвижущая сила гальванического элемента может быть измерена компенсационным методом (рис. 4.2).

Сущность метода компенсации состоит в том, что электродвижущая сила исследуемого элемента уравновешивается падением напряжения от аккумулятора на части АК реохорда АВ.

Для питания реохорда к его концам присоединяют аккумулятор 1. Если проволока АВ на реохорде совершенно однородна, то на единицу длины проволоки приходится падение напряжения Е_ак/АВ.

Для определения э.д.с. исследуемого элемента 2 его присоединяют в боковую цепь так, чтобы направление тока элемента было противоположным току аккумулятора. Передвигая подвижный контакт 8 вдоль проволоки АВ, можно найти такое его положение, при котором падение напряжения аккумулятора на участке АК равно э.д.с. исследуемого элемента. Гальванометр 3 в боковой цепи покажет отсутствие тока, а искомая э.д.с. элемента будет равна: , где Е_х, Е_ак - соответственно электродвижущая сила исследуе­мого элемента и аккумулятора, АК - отрезок проволоки, на котором падение напряжения аккумулятора равно э.д.с. исследуемого элемента.

Рис. 4.2. Схема установки для измерения Э.Д.С.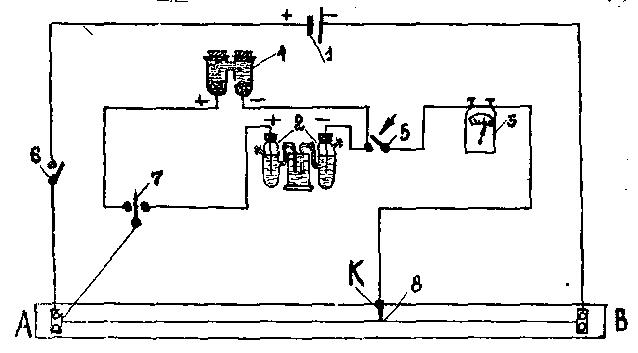

Непосредственно из предыдущего уравнения величина Е_х вычислена быть не может, так как неизвестно значение Е_ак. Чтобы обойти это затруднение, в боковую цепь вместо исследуемого элемента включают нормальный элемент Вестона 4, который обладает хорошо известной и устойчивой э.д.с. Е_о.

Скомпенсировав э.д.с. нормального элемента, получим: , где АВ_о - отрезок проволоки, на котором падение напряжения аккумулятора равно э.д.с. нормального элемента. Проведя преобразования, получим .

По этому уравнению непосредственно можно вычислить величину э.д.с. исследуемого элемента.

Для точных измерений э.д.с. пользуются высокоомными потенциометрами постоянного тока и другими приборами, в основу принципа действия которых положена приведенная ранее компенсационная схема.

Схема экспериментальной установки

Для проведения измерений используется универсальный мультиметр типа UТ-54 (фирма «UNI-T»).