Задание

Для своего варианта статистических данных измерения диаметра проекционной площади наночастиц построить гистограмму и диаграмму кумулятивного распределения, вычислить средний арифметический диаметр, среднее квадратичное отклонение, коэффициент вариации, показатель асимметрии, а также определить моду и медиану распределения.

Контрольные вопросы

1. Какое свойство распределения характеризует среднее арифметическое?

2. Какое свойство распределения характеризует показатель асимметрии?

3. Какое свойство распределения характеризует мода?

4. Какое свойство распределения характеризует среднее квадратичное отклонение?

5. Какое свойство теоретического распределения характеризует стандартное отклонение?

6. Какое свойство распределения характеризует медиана?

7. Почему наряду со средним квадратичным отклонением применяется коэффициент вариации?

8. Зачем наряду со многими другими статистическими характеристиками вычисляют также начальные моменты распределения?

Литература

1. Hunter R.J. Foundations of colloid science. 2nd ed. Oxford: Oxford

University Press, 2001.

2. Barlow R.J. Statistics: a guide to the use of statistical methods

in the physical sciences. Chichester: Wiley, 1989.

3. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и

математической статистики для технических приложений. 3-е изд. Москва:

Наука, 1969.

Вариант 4

d/нм	Ni
10.0–11.9	5
12.0–13.9	7
14.0–15.9	11
16.0–17.9	12
18.0–19.9	24
20.0–21.9	79
22.0–23.9	112
24.0–25.9	189
26.0–27.9	178
28.0–29.9	134
30.0–31.9	79
32.0–33.9	57
34.0–35.9	45
36.0–27.9	35
38.0–39.9	12
40.0–41.9	12
42.0–43.9	8
44.0–46.0	4

Вариант 1

d/нм	Ni
1.33–1.99	8
2.00–2.66	22
2.67–3.32	50
3.33–3.99	82
4.00–4.66	100
4.67–5.32	85
5.33–5.99	43
6.00–6.66	45
6.67–7.32	45
7.33–7.99	13
8.00–8.66	10
8.67–9.32	14
9.33–9.99	9
10.00–10.66	8
10.67–11.32	3
11.33–12.00	1

Вариант 2

d/нм	Ni
1.33–1.99	3
2.00–2.66	6
2.67–3.32	18
3.33–3.99	53
4.00–4.66	87
4.67–5.32	95
5.33–5.99	71
6.00–6.66	67
6.67–7.32	42
7.33–7.99	26
8.00–8.66	14
8.67–9.32	8
9.33–9.99	3
10.00–10.66	3
10.67–11.32	3
11.33–11.99	2
12.00–12.66	2
12.67–13.32	0
13.33–14.00	2

Вариант 3

d/нм	Ni
3.33–6.66	9
6.67–9.99	23
10.00–12.32	68
13.33–16.66	115
16.67–19.99	96
20.00–23.32	80
23.33–26.66	64
26.67–29.99	21
30.00–33.32	14
33.33–36.66	9
36.67–39.99	4
40.00–43.32	3
43.33–46.66	3
46.67–49.99	2
50.00–53.32	0
53.33–56.66	1
56.67–60.00	2

Вариант 6

d/мкм	Ni
0–0.09	7
0.10–0.19	15
0.20–0.29	18
0.30–0.39	28
0.40–0.49	32
0.50–0.59	70
0.60–0.69	65
0.70–0.79	59
0.80–0.89	45
0.90–0.99	38
1.00–1.09	19
1.10–1.20	4

Вариант 5

d/нм	Ni
50–99	29
100–149	109
150–199	211
200–249	372
250–299	558
300–349	440
350–399	307
400–449	223
450–499	139
500–549	81
550–600	31

ЛАБОРАТОРНАЯ РАБОТА № 2

Определение размеров частиц нанодисперсных систем.

Цель работы: Экспериментальное определение размера частиц нанодисперсных систем, подчиняющихся уравнению Релея. (Работа рассчитана на 3 часа)

Краткое теоретическое введение

Для сферических частиц, не проводящих электрического тока, малых по сравнению с длиной волны падающего света и отстоящих друг от друга на достаточно большом расстоянии( разбавленная система) Рэлей вывел следующее уравнение, связывающее интенсивность падающего света I₀ с интенсивностью света, рассеянного единицей объема системы I_p:

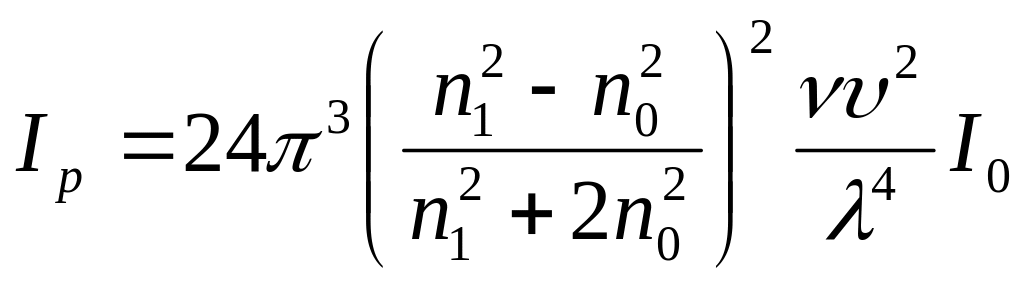, (1)

где n₁ и n₀ - показатели преломления дисперсной фазы и дисперсионной среды; ν-численная концентрация; υ-объем одной частицы; λ-длина световой волны.

Уравнение Релея может быть использовано для определения размеров частиц сферической формы, если их радиус r не превышает 1/20 длины волны λ падающего света. Радиус таких частиц равен:

, (2)

где τ-мутность системы, с- объемная доля дисперсной фазы.

Функция F определяется соотношением:

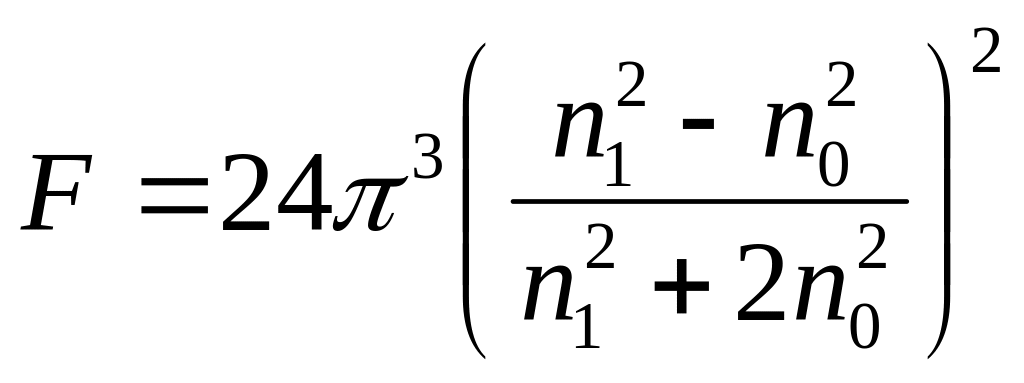(3)

Уравнение Релея лежит в основе оптических методов определения размеров частиц и концентрации дисперсной фазы: ультрамикроскопии, нефелометрии и турбидиметрии.

Ультрамикроскопия от обычной микроскопии отличается тем, что объект ( дисперсная система) освещается сбоку, а наблюдают рассеянный свет. Вследствие этого частицы кажутся светящимися точками на темном фоне, и разрешающая сила микроскопа резко возрастает, что позволяет наблюдать частицы с диаметром до 2-3 нм.

Нефелометрия- метод исследования, при котором измеряют интенсивность рассеянного света, падающего на кювету с дисперсной системой. Обычно объемная концентрация с дисперсной фазы известна или легко определяется. Поэтому соотношение (1) при данной длине волны удобно записать в виде:

, (4)

где k-константа.

Из уравнения (4) следует, что зная концентрацию или размер частиц в стандартной системе, можно рассчитать соответственно размер частиц или их концентрацию в исследуемой дисперсной системе.

Турбидиметрия основана на измерении интенсивности проходящего через дисперсную систему света. Рассеянный свет можно считать фиктивно поглощенным, поэтому есть все основания принять, что закономерности рассеяния света подчиняются уравнению:

, (5)

где I_n –интенсивность света, прошедшего через систему, D = lg I₀/I_п - оптическая плотность; l- толщина слоя системы.

М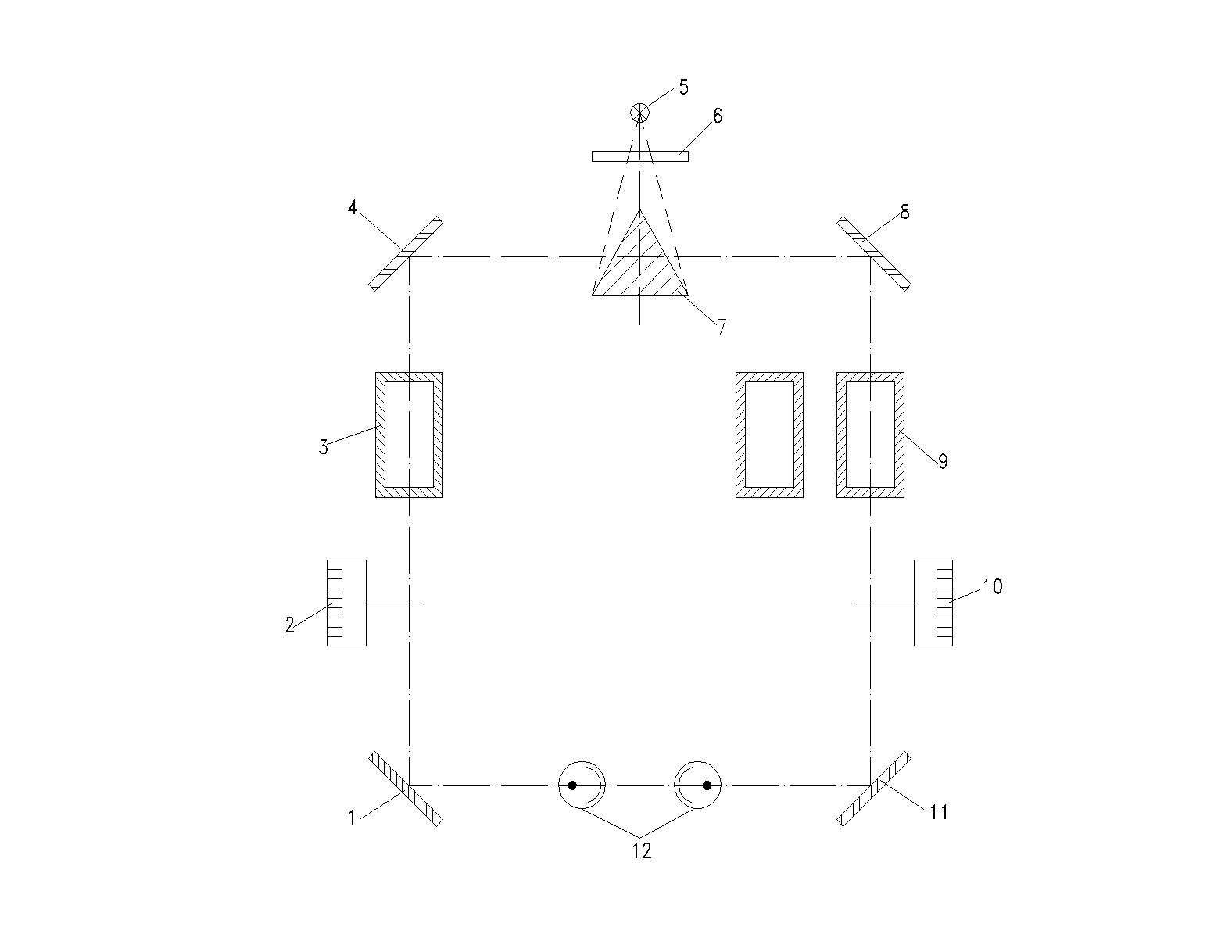 утность τ = I_p/I₀, а отсюда и оптическая плотность D в соответствии с уравнением (1) пропорциональны концентрации и квадрату объема частиц. Это позволяет определять размеры частиц и их концентрацию по оптической плотности системы методом сравнения со стандартными системами с помощью фотоэлектроколориметра. Оптическую плотность золя опре-деляют с помощью прибора ФЭК-56М, оптическая схема которого приведена на рис.1.

Рис.1 Оптическая схема прибора ФЭК-56М: 1,4,8,11- отклоняющие зеркала; 2,10- раздвижные диафрагмы; 3,9- кюветы; 5- источник света; 6- светофильтр; 7- призма;12- фотоэлементы.

Световой луч от источника света 5, пройдя через светофильтр 6, попадает на призму 7, которая делит световой луч на два потока. Отразившись от зеркал 4 и 8, параллельные световые лучи проходят через кюветы 3 и 9, падают на зеркала 1и 11 и затем поступают на фотоэлементы 12. По ходу первого светового луча можно устанавливать последовательно две кюветы (одна с золем, другая с дисперсионной средой).

Раздвижная диафрагма 10, расположенная по ходу правого луча света, при вращении связанного с ней барабана меняет свою площадь и тем самым меняет интенсивность светового потока, падающего на правый фотоэлемент. Раздвижная диафрагма 2, расположенная по ходу левого луча, служит для ослабления интенсивности светового потока, падающего на левый фотоэлемент. При равенстве интенсивностей обоих световых потоков стрелка регистрирующего микроамперметра находится в нулевом положении.

Правый световой луч является измерительным, левый- компенсационным.

Приборы и методы измерений

Измерения оптической плотности золя проводят на фотоэлектроколориметре ФЭК-56М со светофильтром №6 (длина волны в вакууме λ_вак = 540 нм).

Последовательность выполнения работы

1. Включить ФЭК-56М в сеть. Прогреть прибор в течение 10-15 минут.

2. Приготовить золь методом замены растворителя. К 1 мл 1% спиртового раствора канифоли в колбе на 25 мл добавить при встряхивании 10 мл воды.

3. Перенести 1 мл приготовленного золя в колбу на 100 мл и довести дистиллированной водой до метки. Данный раствор имеет кратность разбавления 1:100.

4. Из полученного золя приготовить четыре пробы канифоли с кратностью разбавления 1:1000, 1:2000, 1:5000, 1:10000. Для этого в четыре колбы на 100 мл внести последовательно по 10, 5, 2, 1 мл раствора с кратностью 1:100. Долить в каждую колбу дистиллированной воды до метки.

5. Поставить светофильтр №6. В кюветодержатель поставить две заполненные кюветы: кювету с дистиллированной водой и кювету с очередным раствором ( начиная с наименьшей концентрации). Закрыть крышку прибора и с помощью ручки прибора передвинуть кюветодержатель так, чтобы кювета с дистиллированной водой находилась против фильтра.

6. Поворачивая рукоятку грубой установки вправо (по часовой стрелке) установить стрелку на отметку 100% пропускания ( верхняя шкала прибора).

7. С помощью ручки прибора передвинуть кюветодержатель так, чтобы кювета с раствором находилась против фильтра. Определить оптическую плотность D по нижней шкале прибора. Для каждого образца канифоли измерения провести три раза и определить среднее значение. Записать данные об оптической плотности серии проб в таблицу 1.

Таблица 1. Экспериментальные данные для расчета размеров частиц по уравнению Релея.

Объемная доля канифоли с, см3/см3	Оптическая плотность D	Среднее значение оптической плотности Dср	Мутность τ, м-1	τ/с, м-1

Обработка и оформление результатов

1.Вычислить объемную долю канифоли, используя данные о плотности частиц полимера (плотность частиц канифоли составляет 1.07 г/см³).

2.По формуле (5) рассчитать мутность τ. Полученные данные записать в таблицу.

3.Построить график в координатах τ/с-с. По этому графику экстраполяцией найти величину τ/с при с→0.

4. Полученное значение τ/с при с→0 использовать для расчета радиуса r частицы канифоли по формуле (2). При расчете функции F принять, что показатель преломления дисперсионной среды( воды) n₀ = 1.333, а частиц канифоли n₁ = 1.456. Длину волны в данной среде найти как λ=λ_вак/n₀.

Контрольные вопросы

1. Какие оптические методы используются для определения размеров наночастиц дисперсных систем?

2. Чем обусловлено светорассеяние в дисперсных системах?

3. Для каких дисперсных систем применимо уравнение Рэлея?

Литература

1. Фролов Ю.Г. Курс коллоидной химии. Поверхностные явления и дисперсные системы. Учебник для вузов.-М.: Химия, 1988.

2. Зимон А.Д. Коллоидная химия. М.: Агар, 2007.

3. Коллоидно-химические основы нанонауки. Под ред. Шпак А.П., Ульберг З.Р. Киев. Академпериодика. 2005.466с.

ЛАБОРАТОРНАЯ РАБОТА № 3

Определение размеров частиц нанодисперсных систем, не подчиняющихся уравнению Релея.

Цель работы: Экспериментальное определение размера частиц нанодисперсных систем, не подчиняющихся уравнению Релея, с использованием уравнения Геллера. (Работа рассчитана на 3 часа)

Краткое теоретическое введение

С увеличением размеров частиц закон Релея перестает соблюдаться и интенсивность рассеянного света становится обратно пропорциональной длине волны в степени, меньшей чем четвертая. В этом случае пользуются либо уравнениями, вытекающими из общей теории светорассеяния, либо эмпирическими соотношениями. В частности, если размер ( диаметр) частиц составляет от 1/10 до 1/3 длины световой волны и показатели преломления частиц и среды не сильно различаются, для описания светорассеяния в системе можно воспользоваться следующими эмпирическими уравнениями, предложенными Геллером:

D = kλ^-n и τ = k λ^-n , (1)

где k и k - константы, не зависящие от длины волны.

Зависимости lgD (или lgτ) от lgλ в соответствии с уравнениями (1) представляют собой прямую линию, тангенс угла наклона которой равен показателю степени n с минусом. Значение показателя степени n в этих уравнениях зависит от соотношения между размером частицы и длиной волны падающего света, характеризуемого параметром Z:

Z=8πr/λ (2)

С увеличением Z значение n уменьшается, стремясь в пределе к 2 для частиц, радиус которых больше длины волны. При малых значениях Z соблюдается уравнение Релея и n = 4. Значения n для Z от 2 до 8 приведены в табл.1.

Таблица 1. Показатель степени n в уравнении Геллера

в зависимости от параметра Z .

n	Z	n	Z
3.812	2.0	2.807	5.5
3.686	2.5	2.657	6.0
3.573	3.0	2.533	6.5
3.436	3.5	2.457	7.0
3.284	4.0	2.379	7.5
3.121	4.5	2.329	8.0
3.060	5.0	-	-

Показатель степени n в уравнениях (1) находят на основе турбидиметрических данных. Для этого экспериментально измеряют оптическую плотность системы при различных длинах волн (в достаточно узком интервале λ) и строят график в координатах lgD - lgλ. Показатель n определяют по тангенсу угла наклона полученной прямой. По значению n находят соответствующее значение параметра Z, а затем по формуле (2) рассчитывают средний радиус частиц исследуемой дисперсной системы.

Этот метод, как и уравнение Релея, применим только для « белых » золей, т.е. для неокрашенных дисперсных систем (метод базируется только на светорассеянии).

Приборы и методы измерений

Измерения оптической плотности золя проводят на спектрофотометре.

Последовательность выполнения работы

1. Включить спектрофотометр в сеть. Прогреть прибор в течение 10-15 минут.

2. Измерить оптическую плотность D золя сульфата бария с помощью спектрофотометра, используя светофильтр №3. В кюветодержатель поставить две заполненные кюветы: кювету с дистиллированной водой и кювету с образцом золя. Закрыть крышку прибора и с помощью ручки прибора передвинуть кюветодержатель так, чтобы кювета с дистиллированной водой находилась против фильтра.

3. Поворачивая рукоятку грубой установки вправо (по часовой стрелке) установить стрелку на отметку 100% пропускания ( верхняя шкала прибора).

4. С помощью ручки прибора передвинуть кюветодержатель так, чтобы кювета с раствором находилась против фильтра. Определить оптическую плотность D по нижней шкале прибора. Значение оптической плотности золя должно находиться в пределах 0.70-0.95. Провести еще два измерения и данные об оптической плотности D и средней оптической плотности D_ср для данного светофильтра занести в таблицу 2.

5. Повторить аналогичные измерения оптической плотности D для светофильтров №4-9. Данные занести в таблицу 2.

Обработка и оформление результатов

1. Найти значения lg λ_вак и lg D_ср. Построить график в координатах lg λ_вак - lg D_ср и определить показатель степени n через тангенс угла наклона прямой.

2. По данным таблицы 1 построить график в координатах Z-n, из которого определить значение параметра Z, соответствующее ранее определенному n.

Таблица 2.Экспериментальные данные для расчета размеров частиц дисперсных систем, не подчиняющихся уравнению Релея.

Номер светофильтра	λвак,нм	lg λвак	D	Dср	lg Dср
3	400
4	440
5	483
6	540
7	582
8	620
9	625

3.Рассчитать среднее значение длин волн λ_ср:

4. Полученное среднее значение длин волн λ_ср подставить в уравнение (2) и рассчитать значение среднего радиуса частиц r золя сульфата бария.

Контрольные вопросы

1. Для описания светорассеяния каких систем используется уравнение Геллера?

2. Какие золи называют «белыми»?

3. Какой оптический метод определения размеров наночастиц использован в данной работе?

Литература

1. Фролов Ю.Г. Курс коллоидной химии. Поверхностные явления и дисперсные системы. Учебник для вузов.-М.:Химия, 1988.

2. Зимон А.Д. Коллоидная химия. М.: Агар, 2007.

3. Лабораторные работы и задачи по коллоидной химии.- Под ред. Ю.Г.Фролова и А.С.Гродского.-М.:Химия,1986.

ЛАБОРАТОРНАЯ РАБОТА № 4

Изучение устойчивости гидрозоля гидроксида железа.

Цель работы: Синтез гидрозоля гидроксида железа конденсационным методом; определение порога электролитной коагуляции золя и изучение зависимости его от заряда коагулирующего иона; определение защитного числа стабилизатора (высокомолекулярного соединения). (Работа рассчитана на 3 часа)

Краткое теоретическое введение

Гидрозоль гидроксида железа синтезируют методом конденсации путем проведения реакции гидролиза хлорида железа при 100ºС:

Реакция гидролиза FeCl₃ идет интенсивно с образованием высокодисперсных нерастворимых в воде частиц Fe (OH)₃.

Агрегативная устойчивость золя гидроксида железа обеспечивается, прежде всего, наличием на поверхности дисперсных частиц двойных электрических слоев. Элементарная частица такого золя называется мицеллой. В основе мицеллы лежит нерастворимый в данной дисперсионной среде агрегат, состоящий из множества молекул (атомов): [Fe(OH)₃]_n, где n – число молекул (атомов), входящих в агрегат.

Поверхность агрегата может заряжаться благодаря избирательной адсорбции ионов из дисперсионной среды или диссоциации молекул в поверхностном слое агрегата. В соответствии с правилом Пескова – Фаянса адсорбируются преимущественно ионы, входящие в состав агрегата, либо специфически взаимодействующие с ним. Ионы, сообщающие агрегату поверхностный заряд, называются потенциалопределяющими. Заряженный агрегат составляет ядро мицеллы.

При данном методе получения золя гидроксида железа ядро [Fe(OH)₃]_n·m Fe³⁺ имеет положительный поверхностный заряд за счет адсорбции ионов Fe³⁺ из среды (m – число адсорбированных ионов). Заряд ядра компенсируется эквивалентным зарядом противоположно заряженных ионов – противоионов, расположенных в объеме среды.

Противоионы, находящиеся непосредственно у поверхности ядра (на расстояниях, близких к диаметрам ионов), помимо электростатических сил испытывают силы адсорбционного притяжения поверхности. Поэтому они особо прочно связаны с ядром мицеллы и носят название противоионов адсорбционного слоя (их число m - x). Остальные противоионы составляют диффузно построенную ионную оболочку и называются противоионами диффузного слоя (их число соответствует х).

Мицелла гидрофобного золя является электронейтральной. Формулу мицеллы ионостабилизированного золя гидроксида железа можно записать следующим образом:

агрегат потенциал- противоионы ионы диффузного

определяющие плотного слоя

ионы слоя

_______________________

ядро мицеллы

_________________________________________

коллоидная частица

______________________________________________________

мицелла

В формуле мицеллы границы коллоидной частицы обозначены фигурными скобками. Толщина адсорбционного слоя δ мала ( < 1 нм) и постоянна. Толщина диффузного слоя λ существенно больше (может быть > 10 нм ) и сильно зависит от концентрации электролитов в системе.

По теории Гуи-Чепмена противоионы диффузной части ДЭС распределяются в поле поверхностного потенциала в соответствии с законом Больцмана. Теория показывает, что потенциал в диффузной части слоя снижается с расстоянием по экспоненте. При малом значении потенциала эта зависимость выражается уравнением

φ = φ_δе ^{– χx} (1)

где φ_δ – потенциал диффузного слоя; х – расстояние от начала диффузной части ДЭС; χ– величина, обратная толщине диффузной части слоя.

За толщину диффузной части слоя принято расстояние, на котором потенциал диффузной части слоя φ_δ уменьшается в е раз.

В соответствии с той же теорией толщина диффузной части слоя равна:

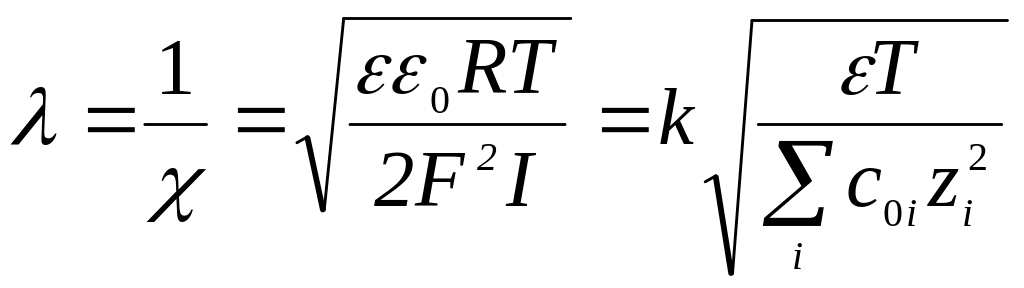(2)

где ε₀- электрическая постоянная; ε- относительная диэлектрическая проницаемость среды; F – постоянная Фарадея; I – ионная сила раствора; c_0i – концентрация иона в растворе; z_i – заряд иона электролита.

Из уравнения следует, что λ уменьшается с ростом концентрации электролита и заряда его ионов и с понижением температуры.

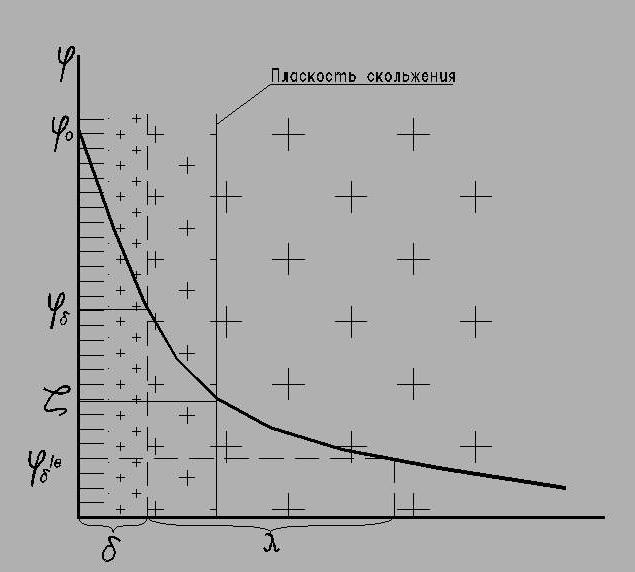При движении одной фазы относительно другой на плоскости скольжения происходит разрыв ДЭС (как правило, в диффузной части) и возникновение электрокинетического («дзета») ζ – потенциала (см. рис 1).

В процессе коагуляции высокодисперсного слоя гидроксида железа образуются сравнительно небольшие по размерам седиментационно-устойчивые агре-

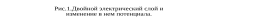
гаты. Поэтому исследование коагуляции частиц Fe(OH)₃ удобнее всего проводить с помощью турбидиметрического метода. Применимость этого метода основывается на сильной зависимости интенсивности светорассеяния от размеров частиц. При коагуляции частиц она повышается, соответственно увеличивается оптическая плотность золя. Поскольку при прохождении светового потока через окрашенные золи часть света рассеивается, а часть поглощается, то при изучении коагуляции в таких системах методом турбидиметрия необходимо исключить поглощение света. Для золя Fe (OH)₃ этого можно достичь, проводя измерения при красном светофильтре, т.е. при длине волны падающего света λ = 620 – 625 нм.

Порог быстрой коагуляции находят по пороговому объему электролита V_к (мл), при котором оптическая плотность золя достигает максимального значения, а при дальнейшем добавлении электролита не изменяется. Значение с_к рассчитывают по формуле:

(3)

где с_к – концентрация введенного электролита, моль/л; V – объем золя, мл.

Для предотвращения агрегации частиц и защиты гидрозолей от коагулирующего действия электролитов применяют высокомолекулярные соединения и коллоидные ПАВ, растворимые в воде, например белки, мыла, крахмал, декстрин. Их стабилизирующее действие основано на образовании на поверхности частиц дисперсной фазы адсорбционных гелеобразных пленок и связано как с уменьшением межфазного натяжения, так и со структурно – механическими свойствами поверхностных слоев.

Защитная способность полимеров или ПАВ относительно выбранного золя характеризуется защитным числом S – количеством вещества, требуемого для стабилизации единицы объема золя. Защитное число S, как и порог коагуляции с_к, определяют методом турбидиметрии. Защитное число S(г/л золя) вычисляют по уравнению:

(4)

где с_ст – концентрация раствора стабилизатора, г/л; V_защ – объем раствора стабилизатора, необходимый для предотвращения коагуляции золя, мл.

При коагуляции электролитами по концентрационному механизму (для сильно заряженных частиц) порог коагуляции с_к обратно пропорционален заряду z коагулирующего иона в шестой степени, т.е

(5)

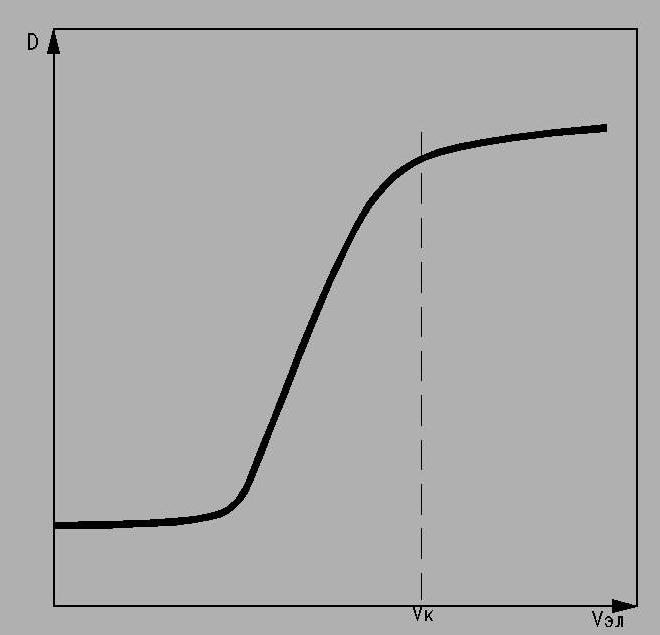
Рис 2. Зависимость оптической плотности D золя от объема электролита – коагулятора V_эл.

Рис 3. Зависимость оптической плотности D золя от объема раствора стабилизатора V_ст.

Значение V_защ соответствует объему стабилизатора в золе, содержащем пороговый объем V_к электролита, при котором на кривой зависимости D = f (V_ст) появляется нижний горизонтальный участок (рис. 3).

Приборы и методы измерений

Фотоэлектроколориметр типа ФЭК – 56М

Электрическая плитка

Коническая колба емкостью 250 мл

Пробирки емкостью 20 мл

Бюретки емкостью 25 мл и градуированные пипетки

2 %-ый (масс.) раствор сульфата натрия

0.5 М раствор ацетата натрия

0.01 %-ый (масс.) раствор желатины

Последовательность выполнения работы

Для получения гидрозоля Fe (OH)₃ в колбу с 250 мл кипящей дистиллированной воды наливают 10 мл раствора хлорида железа. Образовавшийся золь, красно – коричневого цвета, охлаждают до комнатной температуры.

Далее исследуют коагуляцию золя гидроксида железа при введении в него растворов сульфата натрия или ацетата натрия путем измерения оптической плотности полученных систем.

В 10 пробирок наливают по 10 мл золя, воду и электролит (раствор Na₂SO₄ или СН₃СООNa) в следующих объемах:

Номер пробирки … 1 2 3 4 5 6 7 8 9 10

Объем воды, мл ...... 10,0 9,0 8,5 8,0 7,5 7,0 6,5 6,0 5,5 5,0

Объем электролита

V_эл , мл ……………. 0 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0

Электролит вводят в каждую пробу золя за 2-4 мин непосредственно перед измерением ее оптической плотности.

Измеряют оптическую плотность золя в каждой колбе с помощью фотоэлектроколориметра с применением светофильтра № 8 или № 9.

Последовательность выполнения работы

Полученные данные записывают в таблицу 1.

Таблица 1. Результаты исследования коагуляции золя гидроксида железа оптическим методом.

Объем электролита Vэл ,мл	Оптическая плотность золя D
	электролит NaCH3COO	электролит Na2SO4

Строят график зависимости D = f (V_эл) для Na₂SO₄ и CH₃COONa, по нему находят пороговые объемы электролита V_к, вызывающие быструю коагуляцию золя, и по формуле рассчитывают значения с_к. Сравнивают найденные значения с_к для Na₂SO₄ и CH₃COONa и объясняют их в соответствии с правилом Шульце – Гарди [ законом Дерягина – Ландау, см. уравнение (5)].

Затем определяют защитное число полиметра – желатины относительно золя Fe(OH)₃. Для этого готовят 10 проб, наливая в пробирки золь и растворы в следующем объеме и последовательности:

Номер пробирки …………. 1 2 3 4 5 6 7 8 9 10

Объем золя, мл …………… 10 10 10 10 10 10 10 10 10 10

Объем воды

и электролита, мл ……….. до 20 мл, учитывая объемы золя, раствора желатины

Объем раствора

желатины V_ст, мл ………. 5,0 4.0 3,5 3,0 2,5 2,0 1,5 1,0 0.5 0

Объем электролита, мл в объеме, соответствующем V_к

Как и при исследовании коагуляции, общий объем проб должен быть одинаковым и составлять 20 мл. Электролит – коагулятор добавляют через 10-15 мин после введения желатины (для адсорбции желатины на частицах золя). Оптическую плотность золя измеряют через 3-5 мин после введения электролита. Значения D записывают в таблицу (см. табл. 2).

Строят график зависимости D = f (V_ст). Находят объем раствора желатины V_защ, необходимый для предотвращения коагуляции золя, и по формуле (4) рассчитывают защитное число S.

Таблица 2. Экспериментальные данные для определения

защитного числа желатины.

№ пробирки	Объем раствора желатины Vст , мл	Оптическая плотность золя D

Контрольные вопросы

1. Строение двойного электрического слоя коллоидных наночастиц.

2. Факторы, обеспечивающие агрегативную устойчивость наночастиц.

3. Концентрационная и нейтрализационная коагуляция золей под действием электролитов.

4. Правило Шульце-Гарди и закон шестой степени Дерягина-Ландау.

5. Основные положения теории ДЛФО.

6. Влияние электролитов на поверхностные силы и устойчивость наносистем.

7. Адсорбционно-сольватный и структурно-механический факторы устойчивости наносистем.

8. Коллоидная защита. Защитное число стабилизатора.

Литература

1. Фролов Ю.Г. Курс коллоидной химии. Поверхностные явления и дисперсные системы. Учебник для вузов.-М.:Химия, 1988.

2. Зимон А.Д. Коллоидная химия. М.: Агар, 2007.

3. Лабораторные работы и задачи по коллоидной химии.- Под ред. Ю.Г.Фролова и А.С.Гродского.-М.:Химия,1986.

ЛАБОРАТОРНАЯ РАБОТА № 5

Изучение свойств коллоидных дисперсных систем методом капиллярного электрофореза.

Цель работы: Определение электрофоретической подвижности наночастиц дисперсных систем методом электрофореза. (Работа рассчитана на 3 часа)

Краткое теоретическое введение

Все электрические свойства межфазных поверхностей и явления, протекающие на них, обусловлены наличием двойного электрического слоя на границе раздела фаз. Количественные связи между параметрами двойного электрического слоя определяются его строением. На границе соприкасающихся фаз заряды располагаются в виде двух разноименных ионов: ряд потенциалопределяющих ионов на расстоянии, равном их радиусу в несольватированном состоянии, и прилегающий к нему ряд противоионов. Слой противоионов состоит из двух частей. Одна часть примыкает непосредственно в межфазной поверхности и образует адсорбционный слой (слой Гельмгольца) толщиной δ, которая равна радиусу гидратированных ионов его составляющих.

Другая часть противоионов находится в диффузной части – диффузном слое (слой Гуи) толщиной λ, которая может быть значительной и зависит от свойств и состава системы.

Сказанное иллюстрируется на рис. 1, на котором схематически изображено строение мицеллы золя с отрицательно заряженными коллоидными частицами (потенциалопределяющие ионы обозначены знаком «-», противоионные – знаком «+»).

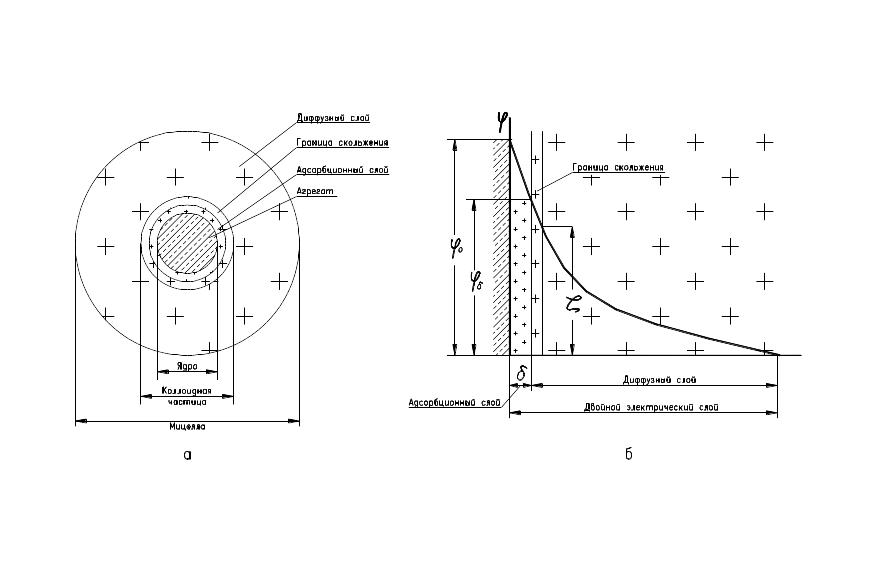
Рис. 1 – строение мицеллы (а) и двойного электрического слоя (б).

Рассмотрим строение мицеллы золя. В центре мицеллы находится кристаллическое тело, названное по предложению Пескова, агрегатом. На нем, согласно правилу Панета – Фаянса, адсорбируются ионы, способные достраивать его кристаллическую решетку. Эти ионы сообщают агрегату электрический заряд и называются потенциалопределяющими. В результате образуется ядро мицеллы, несущее электрический заряд, равный сумме электрических зарядов, адсорбировавшихся на агрегате потенциалопределяющих ионов. Ядро создает вокруг себя электрическое поле, под действием которого к нему из раствора притягиваются противоионы. Часть этих противоионов прочно связана с ядром мицеллы за счет адсорбционных и электростатических сил и образует слой противоионов адсорбционного слоя.

Другая часть противоионов образует диффузный слой противоионов, удерживаемых около ядра только электростатическими силами. Ядро мицеллы вместе с адсорбционным слоем противоионов называется коллоидной частицей (гранулой).

Частица (гранула) вместе с диффузным слоем противоионов образует мицеллу. В целом мицелла электронейтральна.

На границе между ядром и всеми противоионами возникает термодинамический потенциал, а на границе между частицей (гранулой) и диффузным слоем (плоскостью скольжения) возникает электрокинетический потенциал – дзета – потенциал.

При наложении на дисперсную систему внешней разности потенциалов происходит разрыв двойного электрического слоя по плоскости скольжения, в результате чего частица получает определенный заряд и перемещается к соответствующему электроду, а противоионы диффузного слоя – к другому.

Направленное движение частиц дисперсной фазы под действием приложенной разности потенциалов называется электрофорезом.

Скорость электрофореза зависит от дзета - потенциала (электрокинетического потенциала), величина которого определяется по уравнению Гельмгольца – Смолуховского (если радиус частиц много больше толщины двойного электрического слоя):

, (1)

где - вязкость; - относительная диэлектрическая проницаемость среды;

= 8.85419 ∙10^-12 Ф/м - диэлектрическая проницаемость вакуума; u - электрофоретическая подвижность частиц.

, (2)

где u₀ - скорость движения дисперсной среды, Е – градиент потенциала электрического поля.

, (3)

где U – внешний потенциал на электродах; L – расстояние между электродами.

Для определения скорости электрофореза используют следующие методы:

1) микроскопический – заключается в непосредственном определении скорости движения частицы под ультрамикроскопом.

2) макроскопический или метод передвигающейся границы.

В последние два десятилетия в мире отмечен активный интерес к новому интенсивно развивающемуся методу – капиллярному электрофорезу, позволяющему анализировать ионные и нейтральные компоненты различной природы с высокой экспрессностью и эффективностью.

В основе капиллярного электрофореза лежат электрокинетические явления – электромиграция ионов и других заряженных частиц и электроосмос. Эти явления возникают в растворах при помещении их в электрическое поле высокого напряжения.

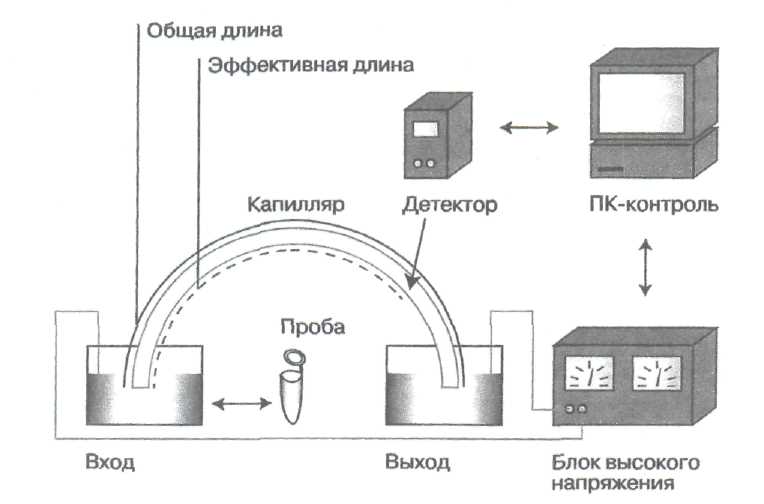
Рис. 2 Устройство системы капиллярного электрофореза.

Если раствор находится в тонком капилляре, например, в кварцевом, то электрическое поле, наложенное вдоль капилляров, вызывает в нем движение заряженных частиц и пассивный поток жидкости, в результате чего проба разделяется на индивидуальные компоненты, так как параметры электромиграции специфичны для каждого вида частиц. В тоже время такие возмущающие факторы, как диффузионные, сорбционные, конвекционные, гравитационные в капилляре существенно ослаблены, благодаря чему достигаются высокие эффективности разделения смеси. Минимальный состав системы, реализующей метод капиллярного электрофореза, должен включать следующие узлы: кварцевый капилляр, источник высокого напряжения, устройство ввода пробы, детектор, систему сбора, обработки и вывода информации (рис.2).

Приборы и методы измерений

Для выполнения работы требуется: система капиллярного электрофореза «КАПЕЛЬ – 103Р» с положительной полярностью высокого напряжения, весы лабораторные типа ВЛР – 200, мерные колбы, пипетки, дозаторы пипеточные, рН - метр лабораторный, стаканы химические, баня водяная.

Реактивы: Нитрат серебра х.ч., боргидрид натрия х.ч., желатина марки «фото А», гидроксид натрия, дистиллированная вода.

Методика измерения

Метод капиллярного электрофореза основан на разделении заряженных компонентов сложной смеси в кварцевом капилляре под действием приложенного электрического поля. Микрообъем анализируемого раствора вводят в кварцевый капилляр, предварительно заполненный подходящим буфером-электролитом. После подачи высокого напряжения (до 30кВ) к концам капилляра компоненты смеси начинают двигаться по капилляру с разной скоростью, зависящей от их структуры, заряда и молекулярной массы и, соответственно, в разное время достигают зоны детектирования.

Идентификацию и количественное определение анализируемых компонентов проводят косвенным методом, регистрируя поглощение в ультрафиолетовой области спектра.

Полученная последовательность пиков называется электрофореграммой (рис.3), качественной характеристикой вещества является время миграции, а количественной – высота или площадь пика, пропорциональная концентрация вещества.

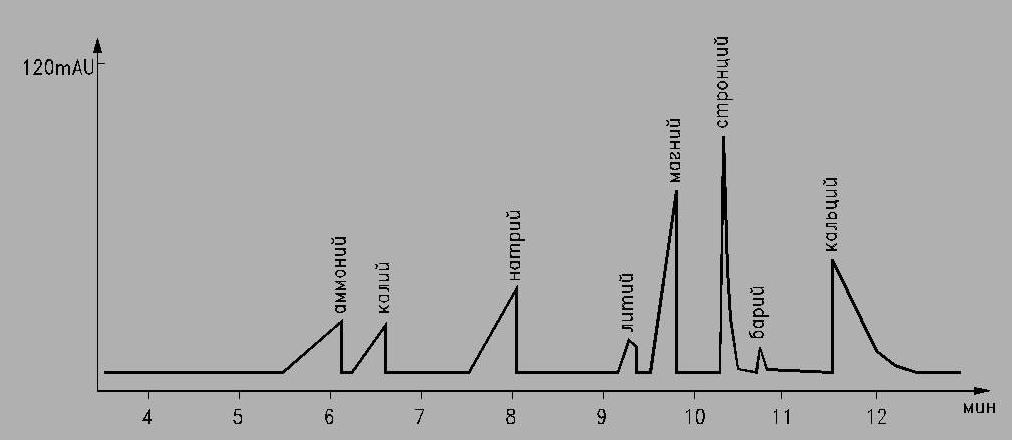
Рис. 3 Электрофореграмма.

(Модельный раствор)

Схема экспериментальной установки

Используемая в данной работе система капиллярного электрофореза «КАПЕЛЬ-103Р» (рис. 4) оснащена фотометрическим детектором и микролинзовой фокусирующей системой. Источник света – ртутная лампа низкого давления с ВЧ- возбуждением, обеспечивающая высокую степень светового потока. В качестве приемника применяется карбид кремневый фотодиод, чувствительный спектра 200-310 нм, в которой присутствует единственная линия ртути 253.7 нм. Этими свойствами обусловлены высокая чувствительность системы, монохроматические условия регистрации и широкий линейный диапазон определяемых концентраций.

Рис. 4 Система капиллярного электрофореза «КАПЕЛЬ – 103Р».

Последовательность выполнения работы

1. Получение золя частиц серебра.

Золь частиц серебра получают реакцией восстановления. К 50 мл раствора AgNO₃ с концентрацией 2·10^-4 моль/л добавляем при перешивании раствор NaBH₄ с концентрацией 2·10^-4 моль/л с объемной скоростью 5 мл/мин. Исходные растворы солей содержат 0,1% желатины (кислотной).

2. Подготовка капилляра к работе.

3. Приготовление вспомогательных и градуировочных растворов.

4. Градуировка системы капиллярного электрофореза «КАПЕЛЬ».

Градуировку системы осуществляют путем измерения сигналов градуировочных растворов. Контроль стабильности градировочной характеристики проводится непосредственно перед измерениями анализируемых образцов путем записи электрофореграмм одной из градуировочных смесей.

5. Выполнение измерений.

Обработка результатов измерений

На основании полученных с помощью программного продукта «МУЛЬТИХРОМ для WINDOWS» данных проводят расчет электрофоретической подвижности по формуле:

, (4)

где L_общ – общая длина капилляра, L_эфф – эффективная длина капилляра, U – приложенная разность потенциалов, t_м – время миграции (время, необходимое компоненту для прохождения им эффективной длины капилляра от зоны ввода пробы до зоны детектирования).

Непосредственно из электрофореграммы нельзя определить электрофоретическую подвижность поскольку время миграции частицы t_м в этом случае равно сумме времен миграции самой частицы и маркера. Из эксперимента можно найти так называемою общую подвижность, которая выражается по формуле u_общ = u_марк + u_эф. Зная из эксперимента u_общ и u_марк можно легко рассчитать u_эф.

Контрольные вопросы

1. Каково строение двойного электрического слоя?

2. Что такое электрокинетический потенциал и как его можно определить?

3. Что такое электрофорез? Как количественно можно охарактеризовать это

явление?

4. Капиллярный электрофорез. Основы метода и его практическое

применение?

Литература

1. Зимон А.Д., Лещенко Н.Ф. Коллоидная химия. Поверхностные явления и дисперсные системы. М: Химия, 1995 (и более поздние издания).

2. Воюцкий С.С. Курс коллоидной химии. М: Высшая школа, 1975.

3. Фролов Ю.Г., Гродский А.С. Лабораторные работы и задачи по коллоидной химии. М: Химия, 1986.

4. Панич Р.М., Воюцкий С.С. Практикум по коллоидной химии и электронной микроскопии. М: Химия, 1974.

5. Комарова Н.В., Каменцев Я.С. Практическое руководство по использованию систем капиллярного электрофореза «КАПЕЛЬ». С-ПЕТЕРБУРГ: ВЕДА, 2006.