ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ

(образован в 1953 году)

Кафедра органической, физической и коллоидной химии Для дистанционного

обучения

Бондарев Ю.М., Зарубин Д.П.,

Козлова Л.В., Павлов А.Н.

Коллоидная химия наночастиц

Лабораторный практикум для студентов

технологических специальностей всех форм обучения

Москва 2008

УДК 547

©Авторы: Бондарев Ю.М., Зарубин Д.П., Козлова Л.В., Павлов А.Н.

Коллоидная химия наночастиц. Лабораторный практикум-М., МГУТУ,2007

Настоящий практикум предназначен для углубленного изучения нанодисперсных систем. Использованы современные физические методы для получения студентами необходимых умений и навыков экспериментальной работы для более полного усвоения и закрепления теоретического материала. Каждая лабораторная работа содержит следующие разделы:

- цель работы,

- краткое теоретическое введение,

- описание приборов и материалов,

-последовательность выполнения работы,

- указания по обработке и оформлению результатов измерений.

Все работы также содержат контрольные вопросы, по которым студент может оценить степень своей теоретической подготовки к защите лабораторной работы.

Авторы: Бондарев Юрий Михайлович, к.х.н., доцент

Зарубин Дмитрий Павлович, к.х.н., доцент

Козлова Лилия Вениаминовна, к.х.н., доцент

Павлов Андрей Николаевич, ст. преподаватель

Рецензент: Антипов Владимир Николаевич, к.х.н., доцент, и.о. зав.каф.

( кафедра физической и коллоидной химии

Московского государственного университета

прикладной биотехнологии)

Редактор: Свешникова Н.И.

© Московский государственный университет технологий и управления, 2007

109004, Москва, Земляной вал,73

Содержание

Работа №1. Анализ распределения частиц по размерам ………..……………………4

Работа №2. Определение размеров частиц нанодисперсных систем………….….….16

Работа №3. Определение размеров частиц нанодисперсных систем,

не подчиняющихся уравнению Релея…………………….………..…….20

Работа №4. Изучение устойчивости гидрозоля гидроксида железа…….……………23

Работа №5. Изучение свойств коллоидных дисперсных систем

методом капиллярного электрофореза…………………………………....28

ЛАБОРАТОРНАЯ РАБОТА № 1

Анализ распределения частиц по размерам.

Цель работы: Для данного распределения частиц построить гистограмму и диаграмму кумулятивного распределения, и определить статистические параметры распределения. (Работа рассчитана на 3 часа)

Краткое теоретическое введение

Важнейшей задачей нанотехнологии является контроль формы и размеров частиц. Для этой цели применяют различные физические методы исследования, несущие информацию об объёме, поверхности или линейных размерах частиц. Наиболее прямым и простым методом является визуальное наблюдение изображения частиц, полученного с помощью электронной микроскопии. Так как реальные частицы имеют три пространственных измерения, а изображение является двухмерным, то каждая частица наблюдается как проекция её трехмерной формы на плоскость. Некоторые методы электронной микроскопии (особенно сканирующая) дают визуальное представление о пространственной форме, однако и в этом случае измерения могут производиться только на плоскости, то есть на плоских проекциях частиц.

М

Рис.1

ножество частиц, синтезированных тем или иным способом, всегда является полидисперсным образцом. То есть, размеры и форма реальных частиц в образце никогда не бывают точно одинаковыми. Если различия частиц считаются не значительными, то образец называют монодисперсным. Но в любом случае, для характеристики образца проводят множество измерений. Из их анализа получают статистические данные об образце. Если частицы имеют одинаковую правильную форму, то проводят измерения в соответствии с этой формой. Например, для сферических частиц проводят измерение диаметра плоского изображения – круга, а для частиц в форме эллипсоида вращения проводят измерения по осям вращения эллипсоида. Если частицы имеют неправильную геометрическую форму, то каждую частицу характеризуют одним размером, выбираемым по определённому методу. Есть несколько таких методов. Они одинаковы во всех видах микроскопии – как в электронной, так и в оптической. Наиболее распространёнными являются следующие.

1) Измерение диаметра Мартина (d_m). Для проекции каждой частицы измеряют длину линии (диаметр Мартина), делящей площадь проекции частицы пополам. Линии проводятся для всех проекций в поле зрения параллельно одному, предварительно выбранному направлению на плоскости изображения (например, на фотографии или на экране монитора). Рис. 1А показывает измерения d_m для трех частиц неправильной формы.

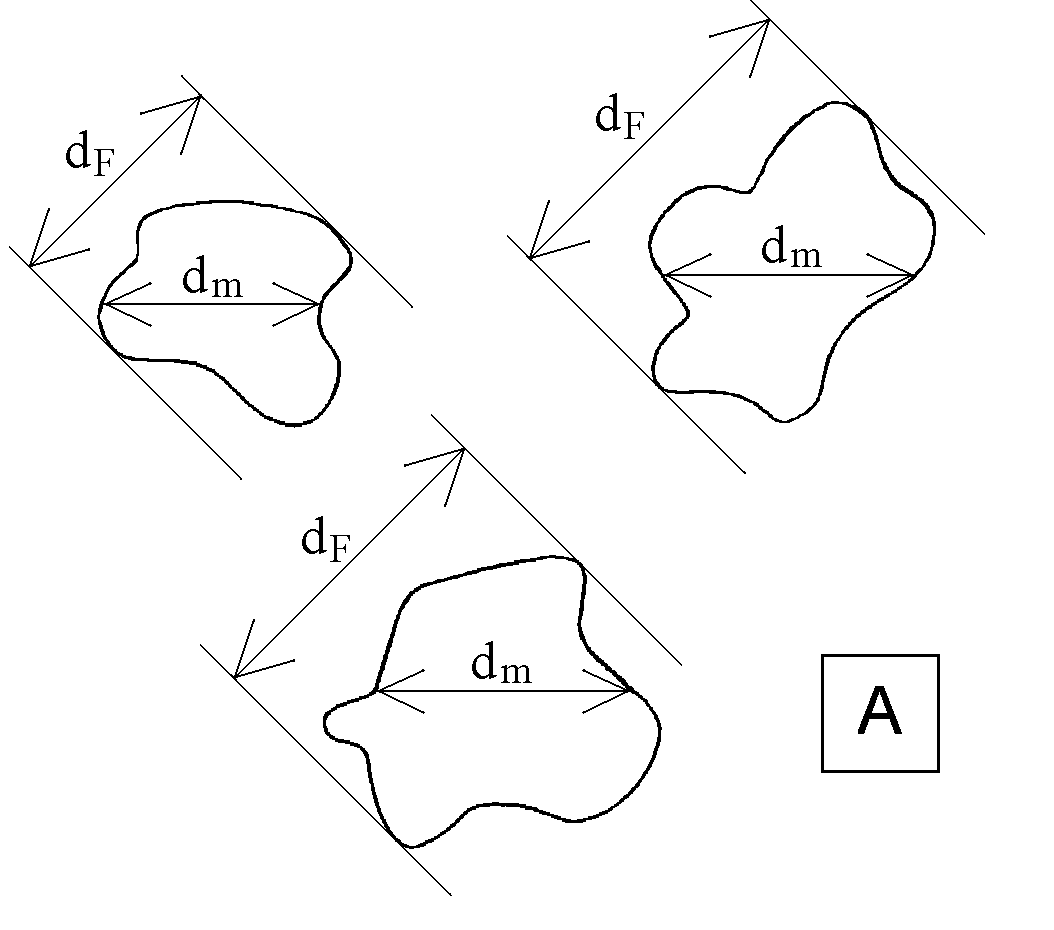
2) Измерение диаметра Фэре (Feret) (d_F). Для проекции каждой частицы измеряют расстояние между двумя касательными к изображению частицы с противоположных сторон. Для всех проекций в поле зрения касательные проводятся параллельно одному, предварительно выбранному направлению на плоскости изображения. Измерения d_F также показаны на рис. 1А.

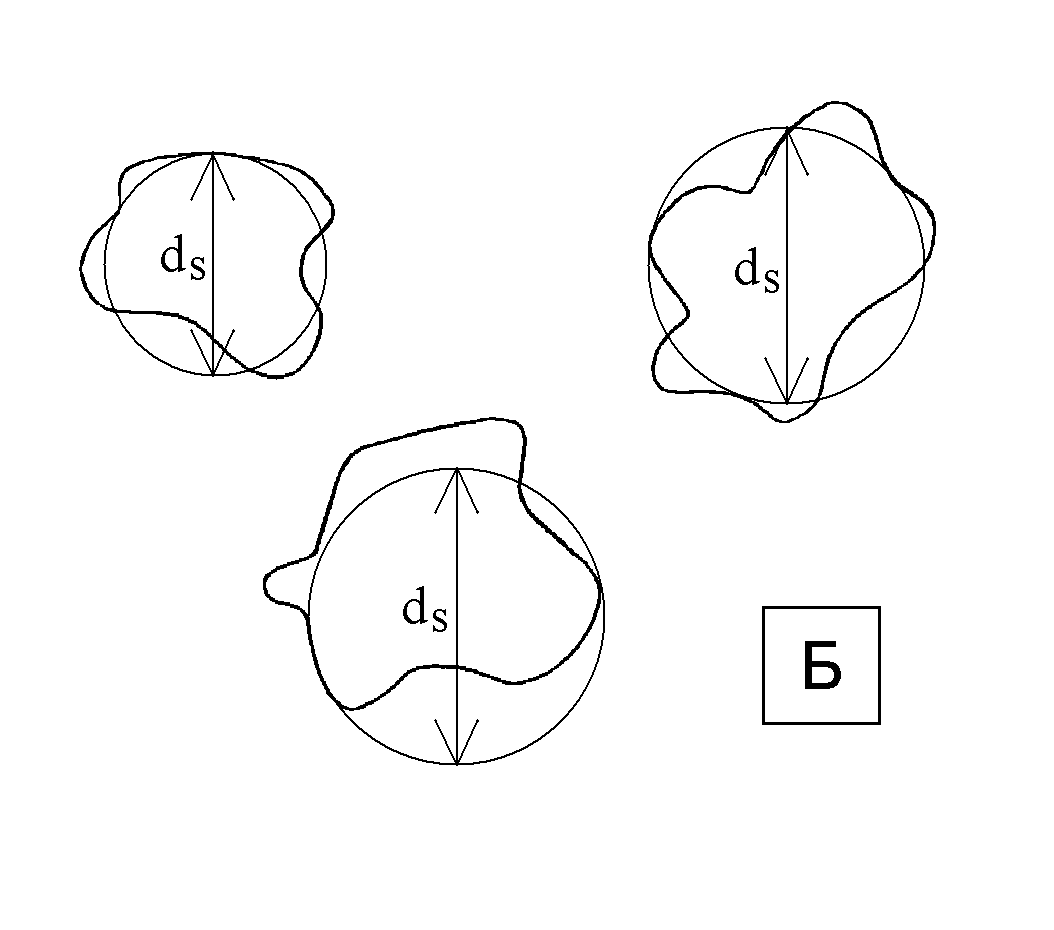
3) Измерение диаметра проекционной площади (d_S). (В курсе коллоидной химии эту величину называют приведённым диаметром). К каждому изображению частицы подбирают окружность такого диаметра d_S, при котором площадь круга равна площади плоского изображения частицы. Рис. 1Б показывает измерение d_S для трех частиц.

Такие измерения могут проводиться вручную, полуавтоматически или автоматически. Число методов в современной практике очень велико. Например, по одному из них, полуавтоматический счётчик направляет на фотографию луч света, дающий освещённый круг. Оператор перемещает или подводит этот круг вручную к очередной частице, регулирует диаметр круга до нужной величины с помощью ирисовой диафрагмы, и нажимает кнопку счётчика. В результате этого, счётчик запоминает диаметр диафрагмы d_S и ставит прокол иглой в центре освещённого круга. Прокол напоминает оператору в дальнейшем, что данная частица уже измерена. До недавнего времени предпочтение отдавали полуавтоматическим счётчикам, которые позволяют проводить измерения не так быстро, но с более высоким качеством. Однако техника, особенно техника компьютерной обработки изображений, постоянно совершенствуется.

Три метода измерений размеров, описанные выше, дают разные оценки размеров частиц одного и того же образца. Но не существует критерия, по которому бы предпочтение отдавалось одному из этих методов. Некоторые приборы позволяют снимать размеры несколькими методами. Считается, например, что отношение среднего диаметра Мартина к среднему диаметру Фэре несёт информацию о средней форме частиц в образце. Поэтому часто измеряют оба этих параметра, наряду с диаметром проекционной площади.

Результаты измерений множества частиц на многих изображениях (фотографиях) из одного образца образуют статистику, по которой можно судить о распределении частиц по размерам. Чтобы получить такую информацию, результаты сортируют по размерам частиц. Например, предположим, что минимальный найденный размер равен 4.2 нм, а максимальный 27.9 нм. Округленный интервал размеров от 4 до 28 нм разбивают на более мелкие интервалы d (их называют также бинами или карманами) и подсчитывают число N_i измерений диаметра, попадающее в каждый интервал. Ширина интервалов должна быть не слишком малой, так чтобы не было пустых интервалов, но достаточно малой, так чтобы распределение было известно возможно подробнее. В качестве примера, табл. 1 показывает статистику одного из исследований. Весь интервал от 4 до 28 нм разбит на карманы одинаковой ширины 2 нм (первая колонка) и подсчитано число частиц N_i, попадающих в каждый карман (третья колонка). При точности измерений диаметра приблизительно 0.5 нм, карманы имеют ширину от 4 до 5.9, от 6 до 7.9 и т.д. Число частиц N_i рассматривается далее как функция диаметра в серединах карманов d_i (вторая колонка). Графическое изображение зависимости N_i от d_i называют гистограммой. (Число N_i по вертикальной оси гистограммы иногда называют счётом). Гистограмма показывает распределение частиц по размерам. Часто вместо распределения абсолютного числа рассматривают распределение относительного числа частиц, которое называют частотой. Частота наблюдения случайной величины (диаметр d_i в данном случае) определяется отношением:

f_i = N_i/N (1)

где N – полное число наблюдений, N = N_i, а N_i – число наблюдений i-той случайной величины (диаметра d_i в i-том кармане). Для рассматриваемого примера, частота вычислена в колонке 4 в табл.1, а на рис. 2А показана гистограмма по данным в табл. 1.

(По горизонтальной оси гистограммы могут откладываться не середины карманов, как на рис.2А, а нижние границы карманов. Столбики гистограммы не обязательно должны примыкать друг к другу вплотную, как на рис. 2. Они могут быть нанесены с зазорами, и могут быть просто вертикальными линиями. Иногда, в учебной практике, проводят плавную кривую через середины столбиков для целей каких либо объяснений, но в научной практике это не принято.)

Табл. 1 Пример обработки статистических данных.

d	di	Ni	f	Fi	fidi
1	2	3	4	5	6	7	8
4–5.9	5	6	0.0035	0.0035	0.0173	0.087	0.43
6–7.9	7	55	0.0315	0.0350	0.2206	1.544	10.81
8–9.9	9	100	0.0578	0.0928	0.5204	4.683	42.15
10-11.9	11	205	0.1185	0.2113	1.3038	14.342	157.77
12-13.9	13	319	0.1842	0.3955	2.3940	31.123	404.59
14-15.9	15	393	0.2272	0.6227	3.4085	51.127	766.91
16-17.9	17	289	0.1668	0.7895	2.8358	48.208	819.54
18-19.9	19	128	0.0740	0.8635	1.4062	26.718	507.63
20-21.9	21	118	0.0682	0.9318	1.4328	30.088	631.86
22-23.9	23	76	0.0439	0.9757	1.0107	23.246	534.66
14-25.9	25	24	0.0139	0.9896	0.3469	8.673	216.83
26-28	27	18	0.0104	1.0000	0.2810	7.587	204.85
		N=1730			15.1781	247.427	4298.04

Рис.2

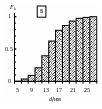
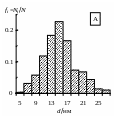
Рис.2

Другой способ характеристики распределения по размерам основывается на вычислении кумулятивной или накопленной частоты. Кумулятивной частотой k-ой величины диаметра называют сумму частот, подсчитанных от d₁ до d_k:

, (2)

где N(d  d_k) – число частиц, диаметр которых меньше или равен d_k. Кумулятивная частота показывает долю частиц, диаметр которых меньше или равен названному диаметру d_k. Для максимального размера она равна 1 (или 100 %). Графическое изображение накопленной частоты в зависимости от измеряемого параметра (диаметра d_k в рассматриваемом примере) называют диаграммой кумулятивного распределения. Для рассматриваемого примера, кумулятивные частоты вычислены в колонке 5 в табл. 1, а на рис. 2Б показана соответствующая диаграмма.

В связи с существованием двух типов диаграмм, распределение частоты f_i иногда называют дифференциальным распределением, а распределение кумулятивной частоты F_k – интегральным распределением.

Диаграммы дифференциального и интегрального распределений дают общее, качественное представление о собранной статистике. Для количественной характеристики вычисляют статистические параметры распределения. К ним относятся, в первую очередь, среднее арифметическое значение измеряемой величины и среднее квадратичное отклонение, а также мода, медиана, дисперсия, коэффициент вариации, показатель асимметрии и эксцесс. Рассмотрим их последовательно.

Среднее арифметическое (или просто среднее) является особенно важной характеристикой. Чтобы понять способ её вычисления при статистической обработке, отвлечемся на время от размеров частиц, и обратимся к более простому примеру. Предположим, что группа студентов 11 человек получили экзаменационные оценки 3, 4, 4, 3, 5, 4, 3, 4, 5, 4, 3 – записанные соответственно алфавитному списку группы. Если обозначить оценки х_j, то средняя оценка_х находится по простой формуле:

(3)

где j – порядковый номер оценки в списке, N – общее число оценок, 11. (Получается_х = 3.8). С другой стороны, оценки можно отсортировать по карманам и записать {(3,3,3,3),(4,4,4,4,4),(5,5)} – 4 тройки, 5 четвёрок и 2 пятёрки. Соответственно этому, можно вычислить:

=(3+3+3+3+4+4+4+4+4+5+5)/11=(4×3+5×4+2×5)/11 = (4/11)×3 +(5/11)×4 +(2/11)×5=3.8.

Этот способ вычисления описывается формулой:

(4)

где i – порядковый номер кармана, N_i – число одинаковых оценок x_i в кармане i , f_i – частота наблюдения оценки x_i, находящейся в i-ом кармане.

Формулы (3) и (4) эквивалентны, но при статистической обработке всегда применяют формулу (4) для сортированных данных. В применении к размерам частиц d_i две формулы имеют вид:

(5)

Обратившись к гистограмме на рис.2А, можно увидеть, что f_i – это высота столбца гистограммы при соответствующем i-ом диаметре d_i. Поэтому среднее арифметическое имеет смысл центра тяжести гистограммы. Например, если мы хотим вырезать гистограмму и приколоть её одной кнопкой к вертикальной стене так, чтобы ось d была точно горизонтальной, то кнопку нужно прикалывать именно на расстоянии_d по горизонтальной оси. Относительно этой координаты вращающий момент гистограммы в плоскости чертежа равен нулю.

Дисперсией D результатов измерений называют средний квадрат отклонения от среднего. В применении к диаметру d_i эта величина определяется формулой:

, (6)

где j – номер измерения d_j в общем списке, i – номер интервала (кармана) в сортированном списке, N_i – число частиц в данном интервале, f_i – частота,_d – среднее арифметическое.

Величина дисперсии показывает степень разброса измеренных значений d_i относительно среднего_d или, другими словами, является мерой ширины распределения. Она имеет размерность квадрата размерности d_i. Например, если результаты измерений d_i выражаются в единицах длины нанометрах, то дисперсия выражается в единицах площади нанометр². Поэтому вместо дисперсии намного чаще применяют корень квадратный из неё. Соответствующую величину называют средним квадратичным отклонением:

. (7)

Эта величина имеет ту же размерность, что d_i. Она применяется настолько чаще, чем дисперсия, что дисперсию часто обозначают s², а не специальным символом D. Как и дисперсия, она характеризует степень разброса данных относительно среднего. Важно заметить, что одна и та же величина s может расцениваться как большая или маленькая в зависимости от величины среднего. Например, среднее квадратичное отклонение s = 5 нм при_d = 10 нм может считаться большим, означающим широкое распределение, но та же величина s = 5 нм при_d = 1000 нм означает узкое распределение. В связи с этим применяется также относительная характеристика, равная отношению среднего квадратичного отклонения к среднему арифметическому. Её называют коэффициентом вариации:

(8)

Часто эту величину выражают в процентах.

Среднее квадратичное отклонение имеет глубокий смысл, следующий из теории математической статистики. Предположим, что число частиц в образце бесконечно велико, и что проведено бесконечно большое число измерений N  . Если на гистограмме (рис.2А) при последовательном увеличении N уменьшать одновременно ширину карманов d, то в пределе N   и d  0 гистограмма превратится в плавную кривую, называемую теоретическим распределением. Также в пределе N   и d  0 :

1) частота наблюдений f_i превращается в плотность вероятности f(d), интеграл которой в пределах от d₁ до d₂ равен вероятности наблюдения частиц с диаметрами в этом интервале,

2) гистограмма превращается в график функции плотности вероятности,

3

Рис.3

) кумулятивная частота F_k превращается в кумулятивную (накопленную) вероятность F(d), равную вероятности наблюдения частиц с диаметром от 0 до данного диаметра d_k,

4) среднее арифметическое превращается в величину, называемую математическим ожиданием :

5) среднее квадратичное отклонение превращается в величину, называемую стандартным отклонением :

Считается, что каждая ограниченная статистика (при малом N) имеет своё теоретическое распределение, которое точно не известно, но о котором мы составляем представление по результатам данного числа измерений N. Одним из наиболее важных теоретических распределений является нормальное распределение или распределение Гаусса. Оно описывается функцией плотности вероятности:

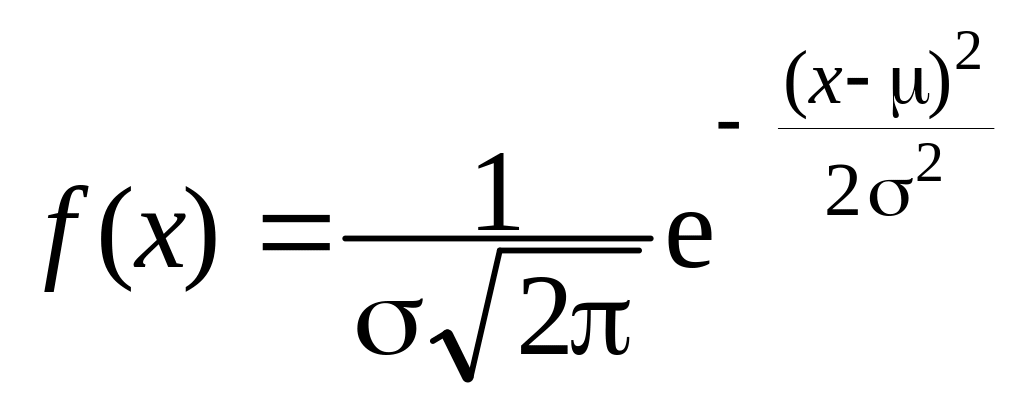или . (9)

Например, известно, что рост взрослого человека распределен (в большой популяции людей) в соответствии с этим законом (если рост обозначить х), но вес человека – не по этому закону. Размеры частиц также часто распределены приблизительно нормально, но это зависит от метода и условий синтеза частиц.

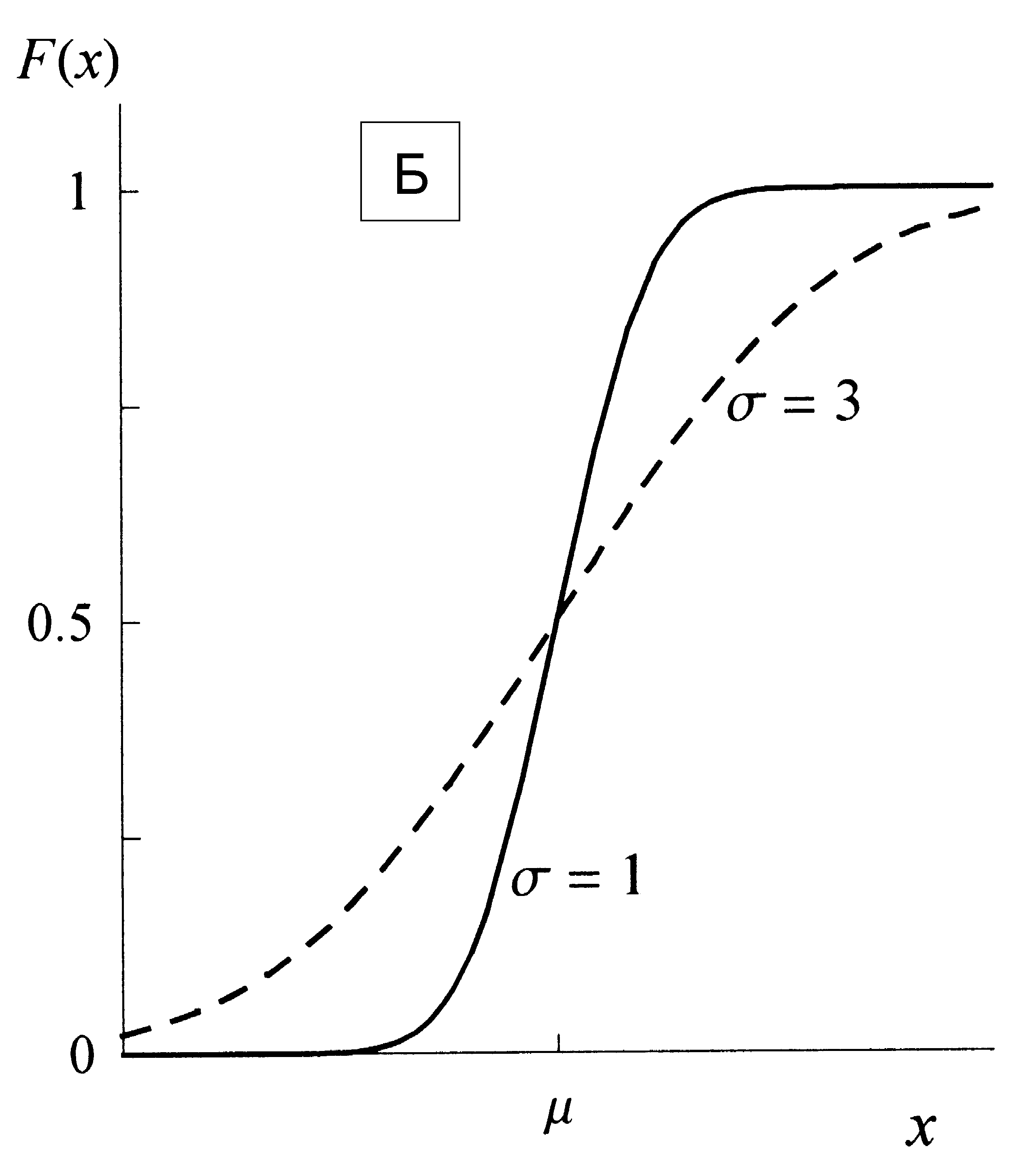
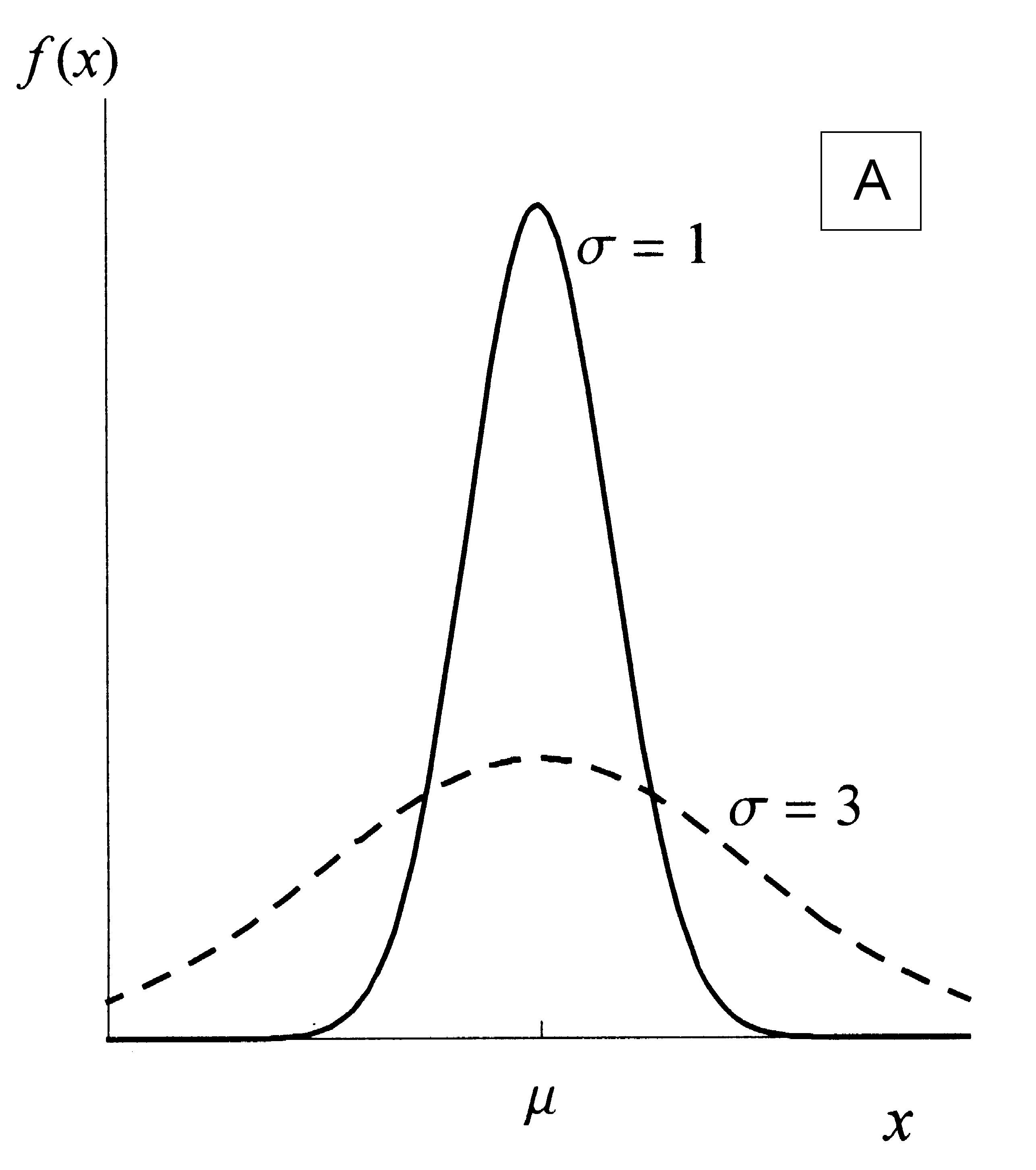
Распределение Гаусса является симметричным, с центром симметрии при математическом ожидании . Ширина функции плотности вероятности определяется стандартным отклонением . На рис. 3А показаны два графика функции (9) с одинаковыми  и разными . (Величина  определяет положение графика вдоль горизонтальной оси х.) Так как интеграл f(x) в любом интервале х равен вероятности наблюдения х в этом интервале, то площадь под всем графиком от – до  равна 1. (Коэффициент перед функцией ехр в (9) обеспечивает это свойство; он называется нормирующим множителем.) Площадь под графиком в интервале  ±  равна 68.3...% от всей площади, в интервале  ± 2 равна 95.5...%, а в интервале  ± 3 равна 99.7...%. Соответственно, вероятность наблюдения х в интервале  ±  равна 0.683..., в интервале  ± 2 равна 0.955..., а в интервале  ± 3 равна 0.997.... (Вероятность не принято выражать в процентах.)

Поэтому, если гистограмма (при ограниченном N) приблизительно симметрична, то обычно считают, что среднее квадратичное отклонение s показывает интервал_х ± s (или_d ± s для диаметра), в пределах которого находится приблизительно две трети всех результатов измерений.

Распределение частиц по размерам далеко не всегда является симметричным. Для характеристики степени отклонения от симметричности применяют величину, называемую показателем асимметрии (или коэффициентом асимметрии):

. (10)

В случае распределения, симметричного относительно среднего арифметического, среднее арифметическое отклонений d_i –_d , возведённых в любую нечетную степень, равно нулю. Поэтому показатель асимметрии также равен нулю в этом случае. Для несимметричного распределения показатель асимметрии больше нуля, если распределение вытянуто в большей степени в сторону d_i _d (в сторону больших d), и меньше нуля в противном случае.

Если А = 0, то гистограмма симметрична, и в этом случае максимум частоты на гистограмме находится при d =_d. Но если A  0, то гистограмма не симметрична относительно_d, и диаметр, соответствующий максимуму гистограммы, не совпадает с_d. В таких случаях возникает неопределённость в том, что следует считать "центром" распределения. Поэтому наряду со средним применяются также другие характеристики "центра" распределения. К ним относятся мода и медиана.

Модой распределения называют координату максимума частоты. В случае распределения частиц по размерам, мода M (или модальный размер) показывает, какой размер частиц встречается наиболее часто. Обычно теоретическое распределение имеет один максимум, и тогда его называют одномодальным. Иногда оно имеет два максимума – двухмодальное распределение. Гистограмма может иметь два или более ложных максимума, если сортировка данных проведена так, что в карманах находятся слишком малые числа наблюдений N_i. В этом случае, максимумы являются ложными. Они не означают более одной моды у теоретического распределения.

Медианой распределения называют координату кумулятивной частоты 0.5 (или 50%). В случае распределения частиц по размерам, медиана m (или медианный размер) имеет свойство, что половина частиц имеют размер d  m, и половина частиц имеют размер d  m. Смысл этой величины можно дополнительно пояснить на примере экзаменационных оценок, упоминавшихся выше, {(3,3,3,3),(4,4,4,4,4),(5,5)}. Всего оценок 11, шестая оценка (в середине списка) равна 4, поэтому медианная оценка равна 4.

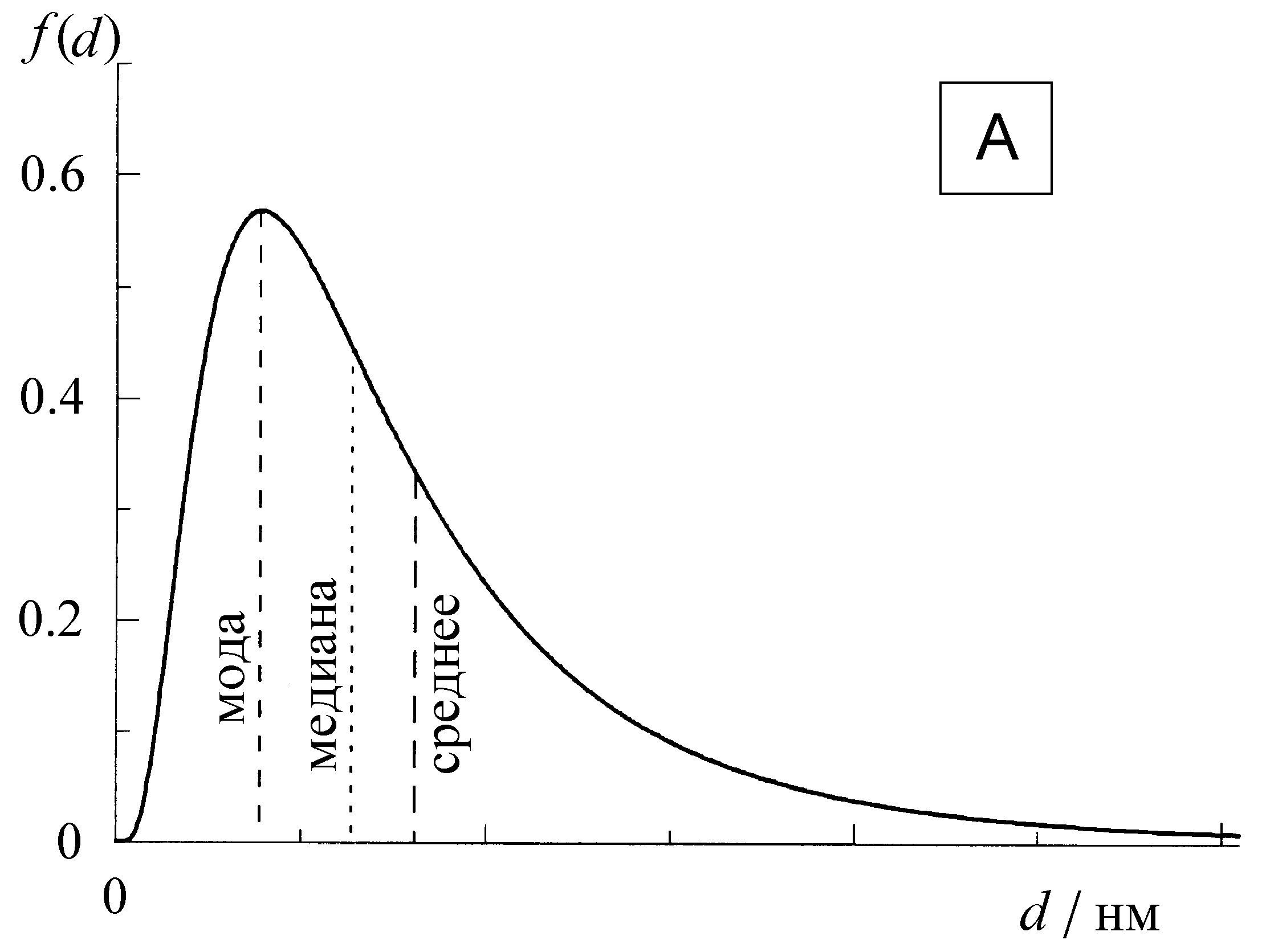
Таким образом, среднее арифметическое имеет свойство центра тяжести гистограммы, мода представляет собой координату максимума гистограммы, а медиана – координату кумулятивной частоты 0.5. Если распределение симметрично, то все три характеристики совпадают, а если не симметрично, то не совпадают. При не симметричном распределении медиана обычно (но не всегда) находится между модой и средним арифметическим. Это соотношение показано на примере теоретического распределения на рис. 4А и Б. (Такое распределение называется логарифмическим нормальным, или логнормальным. В случае размеров частиц, оно часто наблюдается, когда образец получают механическом истиранием более крупных частиц).

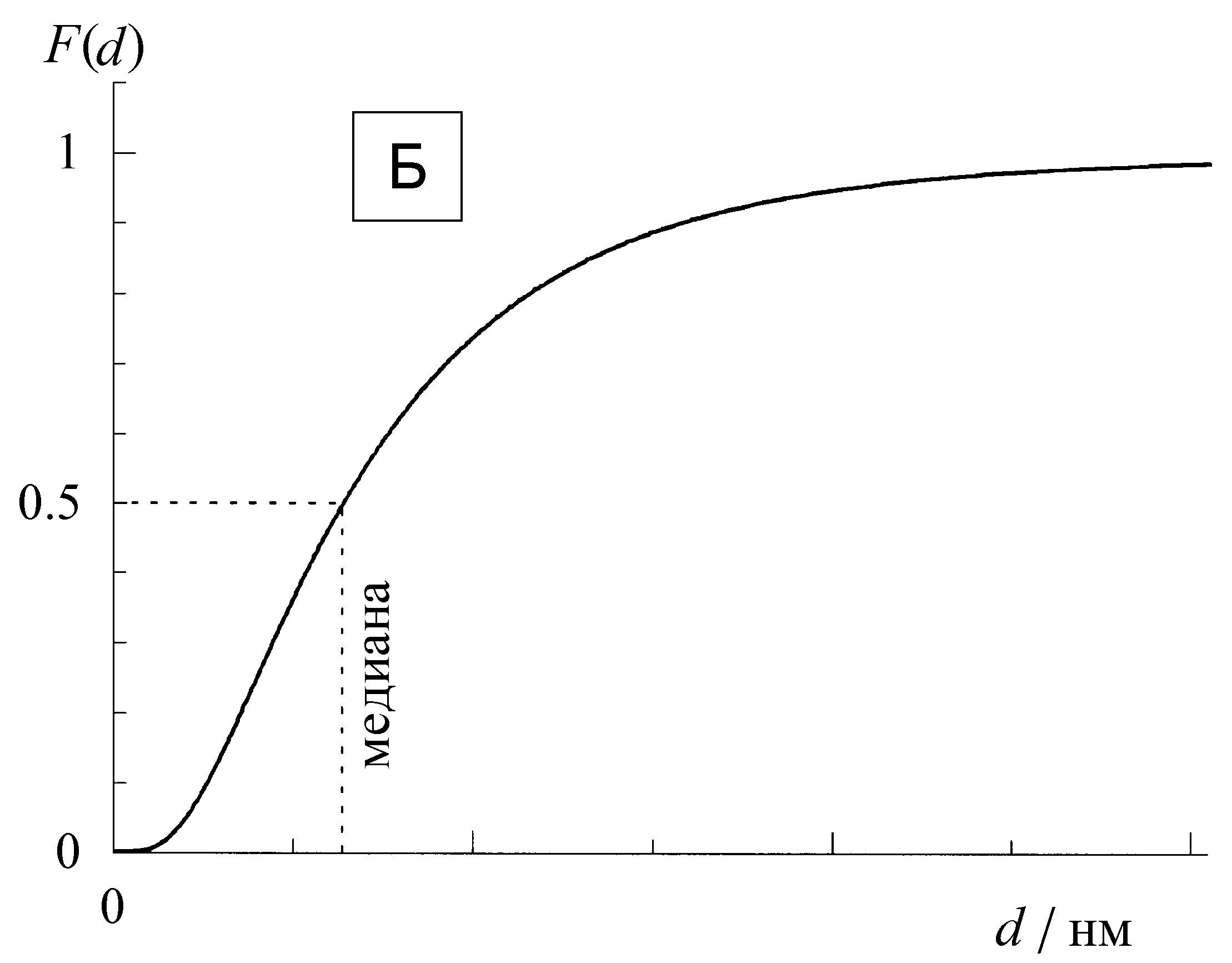Следует заметить, что все статистические параметры, полученные при ограниченном числе измерений N, являются случайными. То есть, если из очень большого образца частиц повторно выбирать N штук, каждый раз проводя N измерений, и каждый раз вычисляя параметры_d, D, s, A, М, m, то будут получаться не точно одинаковые результаты. Они становятся одинаковыми только в пределе N   и d  0. Поэтому малая величина A по результатам одной статистики не обязательно означает, что теоретическое распределение не симметрично. Чаще всего оказывается, что А  0, но средний, модальный и медианный размеры совпадают в пределах точности сортировки данных по размерам (то есть, все три приходятся на один карман гистограммы). На практике, среднее арифметическое считается более важной характеристикой, тогда как мода и медиана упоминаются, если распределение заметно отличается от нормального.

Н

Рис.4

аконец, существует ещё одна характеристика формы теоретического распределения. При данной величине стандартного отклонения , максимум функции плотности вероятности может быть более или менее острым (или более или менее плоским). Мерой этого служит характеристика, которую называют эксцесс. При ограниченном числе N наблюдений размеров частиц d, эксцесс вычисляется по формуле:

.

В случае нормального распределения, дробь в правой части формулы равна 3, поэтому эксцесс равен 0. У других распределений он может отличаться от нуля. Положительный эксцесс указывает на более плоский максимум, чем у распределения Гаусса при данном . Однако эта характеристика применяется редко.