2.2 Оценка параметров нагружения
Если принять, что
состояние материала перед фронтом
ударной волны описывается параметрами
,
а за фронтом
(давление,
плотность, относительная внутренняя
энергия материала, объем материала,
скорость частиц), то из закона сохранения
массы, импульса и энергии следует, что
,
где
–
скорость ударной волны, или
.
Поскольку удельная
внутренняя энергия является функцией
давления и удельного объема
,
это уравнение представляет геометрическое
место точек на плоскости
,
состояние которых достигается при
прохождении ударной адиабаты, т.е. это
ударная адиабата – кривая Гюгонио.
Обычно в эксперименте измеряется
скорость свободной поверхности, с
помощью которой определяется массовая
скорость за фронтом ударной волны (она
равна скорости свободной поверхности),
и скорость ударной волны.
Зависимость между
скоростью ударной волны и массовой
скоростью за фронтом волны можно
представить уравнением прямой:
;
она может быть использована в диапазоне
давлений от 10 до 100 ГПа. Константы прямой
и
определяют из экспериментальных данных.
При получении плоской волны путем метания пластины без учета упругого предвестника и многоволновой конфигурации схематическая модель расчета параметров может быть представлена, как показано на рисунке 5.
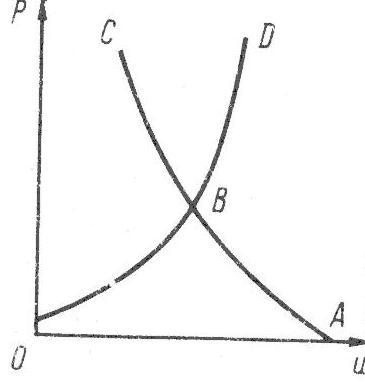
Рисунок 5 – P–u-диаграмма для случая плоская волна – метаемая пластина
Уравнение ударной
адиабаты будет иметь следующий вид:
,
где
– исходная плотность образца-мишени;
– константы материала-мишени.
Поскольку метаемая
пластина замедляется от скорости
до
скорости
,
уравнение для нее будет
,
где
–
константы материала пластины;
–
скорость полета пластины.
Из этих уравнений
можно аналитически определить
.
Уравнение можно решать графически,
находя точку пересечения
диаграммы для образца и зеркального
отображения
диаграммы метаемой пластины (рисунок
3.8). Исходное положение образца определяется
координатами
и
,
а ударника
и
.
При одинаковых материалах образца и
пластины их ударные адиабаты симметричны
и их массовая скорость равна половине
скорости удара.
Тот же подход может
быть использован для определения
давления при плоской ударной волне,
реализуемой контактным взрывом (рисунок
6). Рассматривается случай, когда
акустическое сопротивление металла
превышает акустическое сопротивление
продуктов взрыва, что характерно для
большей части металлов. Полагая, что
исходная плотность металла
и параметры
и
потока из продуктов взрыва за детонационной
волной известны, определяют
и
.
В этом случае давление и скорость на
фронте двух волн
,
должны
соответствовать точке пересечения
ударных адиабат металла и продуктов
взрыва, построенных в плоскости
Аналитическое выражение дается из законов сохранения количества движения и массы.
Рисунок 6 –Давление при контактных взрывах. Плоская волна.
Часто на практике требуется получить большую глубину упрочнения. Тогда используется схема упрочнения в косой ударной волне. Эта схема проще для реализации, поскольку не требует специального генератора. Рассмотрим схему с контактным взрывом для случая, когда импульс давления распространяется по обрабатываемой поверхности со скоростью, превышающей скорость распространения упругих волн. Он наиболее характерен при использовании достаточно мощных взрывчатых веществ, когда достигается максимальный эффект упрочнения.
Схема движения детонационной волны показана на рисунке 7. В области I находится еще не сдетонировавшее ВВ., ОС – волна детонации, движущаяся со скоростью D по упрочняемой поверхности, область II – расширяющиеся продукты взрыва, ЕО – начальная граница металл- ВВ. Под действием продуктов взрыва металл деформируется по кривой ОВ – границе между продуктами взрыва и металлом. Ударная волна распространяется в металле по кривой ОА, наклоненной к оси абсцисс под углом и воздействует на металл в области III. Аналитическое выражение дается из законов сохранения массы и импульса при переходе через косой скачок.
Рисунок 7 – Модель к расчету параметров упрочнения бегущей ударной волной: / - в.в.; // - продукты взрыва; /// - область нагруженного металла; IV - ненагруженный металл