Материалы, оборудование, приборы

1. Материалы: плита древесностружечная, шпон строганный, карбамидоформальдегидная смола, хлористый аммоний.

2. Оборудование и приборы: лабораторный гидравлический пресс для горячего склеивания, весы аналитические, металлические поддоны, секундомер, стаканы химические.

Порядок выполнения работы

1. Ознакомиться с устройством лабораторного клеильного пресса, с правилами техники безопасности при работе на нем.

2. Приготовить требуемое количество рабочего раствора клея.

3. Приготовить рубашки из шпона строганного.

4. Отрегулировать температуру и давление на лабораторном прессе.

5. Нанести рабочий раствор связующего на листы шпона.

6. Сформировать пакет.

7. Произвести облицовывание в лабораторном прессе.

8. Визуально определить качество облицованной детали.

Содержание отчета

1. Наименование и цель работы.

2. Основные понятия и определения.

3. Рецепт клея.

4. Технологический режим облицовывания ДСтП строганым шпоном.

5. Выводы.

Контрольные вопросы

1. Что такое облицовывание щитов?

2. Характеристика применяемых материалов.

3. Подготовка древесностружечной плиты к облицовыванию.

4. Подготовка облицовок из шпона строганного.

5. Рецепт клея.

6. Режимы облицовывания.

7. Дефекты облицовывания.

ЛАБОРАТОРНАЯ РАБОТА № 9

Определение точности обработки деталей

Цель работы: практическое ознакомление студентов с методом статистического контроля точности обработки деталей на деревообрабатывающих станках.

Точность обработки - это степень соответствия обработанной детали ее номинальному размеру и заданной форме. То или иное отклонение от заданного размера или формы является характеристикой погрешностей обработки. Погрешности, которые обычно имеют место при обработке деталей, могут быть систематическими или случайными. Систематические погрешности делятся на два вида:

1. Погрешности, остающиеся постоянными в процессе обработки партии деталей.

2. Погрешности, закономерно изменяющиеся в процессе обработки.

К первым относят погрешности обработки, являющиеся следствием геометрических погрешностей станка, инструмента или приспособления.

Ко вторым относятся погрешности, вызванные постепенным износом режущего инструмента в процессе работы, нагревом станка и режущего инструмента.

Случайные погрешности характеризуются рассеиванием размеров деталей в партии. К числу случайных погрешностей могут быть отнесены погрешности, вызываемые неоднородностью материала, неодинаковой величиной припусков, колебанием режимов обработки.

При определении результирующей погрешности точности обработки используется статистический метод, основанный на законе больших чисел. Все случайные погрешности подчиняются определенной закономерности. Проблема определения случайных событий разрешена Гауссом, который вывел закон нормального распределения событий.

Этот закон отвечает формуле:

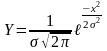, (7)

где  – среднеквадратичное отклонение от среднего значения (центр группирования размеров);

Y – частота появления погрешности;

ℓ - основание натурального логарифма;

X – погрешность размера, отсчитываемая от центра группирования.

Среднее значение, или центр группирования размеров:

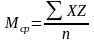, (8)

где X – среднее значение интервала;

Z – число замеров заготовок, находящихся в данном интервале;

n – количество всех размеров.

Величина М совпадает с центром группирования, около которого, в основном, располагаются значения размеров партии.

Но это среднее арифметическое дает представление о средней точности обработки, но не выражает пределов их колебания.

Поэтому определяется среднеквадратичное отклонение:

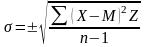. (9)

Знаки ± показывают, что отклонение может быть как в ту, так и в другую сторону от центра группирования М.

При сравнении двух средних арифметических, выраженных в равных единицах, не достаточно знать среднее квадратичное отклонение. Вводится еще понятие коэффициента изменчивости:

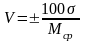, % . (10)

Полученный результат среднего арифметического М не может точно характеризовать величину данного свойства, так как если мы получим несколько очень больших или очень малых результатов измерения, то они повлияют на величину М. Вводится еще понятие средней ошибки среднего арифметического, которая позволяет по частному значению арифметического судить об общей его величине:

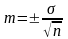. (11)

Среднюю ошибку можно выразить в процентах от среднего арифметического:

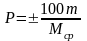, % . (12)

Это показатель точности. Он характеризует надежность результатов опыта. Показатель точности должен быть меньше 5 %.