Министерство образования Российской Федерации

Московский государственный технический университет имени Н.Э. Баумана

Методические указания

к выполнению домашнего задания

по дисциплине

«Механика сплошной среды»

Кафедра ИУ-10 «Защита информации»

Москва, 2008

Утверждено на заседании кафедры ИУ-10 «Защита информации» протокол №01/07 от 03.09.2007.

Домашняя работа по дисциплине “Механика сплошной среды” выполняется на 3-м семестре.

Указания к выполнению:

Номер варианта соответствует порядковому номеру студента в журнале группы. Промежуточные результаты необходимо округлять не более чем до 5-го знака после запятой (лучше не округлять). Результат записывать с округлением до первого знака после запятой.

Задачи на тему: “Статика”

Задача №1

Условие задачи:

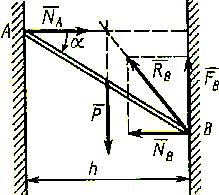
Однородный тяжелый стержень АВ длиной l опирается концом А на гладкую вертикальную стену, а другим В—на шероховатую вертикальную стену (рис.1). Расстояние между стенами h<l. Определить коэффициент трения стены f, при котором возможно равновесие стержня.

№ вар.	h, см	l,см
1	10	15
2	5	20
3	7	24
4	14	22
5	18	29
6	15	23
7	12	17
8	13	15
9	8	25
10	9	19
11	6	21
12	8	20
13	11	26
14	17	27
15	13	22

Решение:

Рассмотрим случай, когда точка А расположена выше точки В стержня. Равновесие стержня невозможно, если точка А расположена ниже точки В. На стержень действуют сила тяжести P, приложенная посередине стержня нормальная реакция гладкой стены N_A и реакция шероховатой стены R_B , которую разложим на нормальную реакцию N_B и силу трения F_B.

Составим условия равновесия плоской системы сил:

; N_A-N_B=0;

; F_B-P=0;

;

Рис. 1

К этим условиям следует добавить неравенство для силы трения

F_B fN_B.

Из уравнений равновесия находим

N_A = N_B = N; F_B = P; N=N_A = Ph/(2lsinα).

Из геометрических условий задачи имеем

Итак, для силы трения F_B имеем следующие уравнение и неравенство:

Исключая из них силу трения F_B, после сокращения на Р получаем

Искомое условие для коэффициента трения f при равновесии стержня принимает вид

Задача №2

Условие задачи:

Изогнутый под прямым углом стержень ABDC находится в горизонтальной плоскости. Стержень закреплен с помощью подпятника А и подшипника В (рис. 1). На стержень под прямым углом жестко насажен диск радиуса R = 0,5м. В плоскости диска по касательной действует сила S под углом γ=30° к вертикали. В точке С стержня приложена сила Р=20 кН под углом α=60° к вертикали и углом β= 60 к линии СК, которая находится в плоскости Axz. Определить силы реакций подпятника и подшипника, а также значение силы S, необходимой для равновесия.

№ вар.		2	l3	l4
16	1	1	0.5	1.5
17	2	2	1,5	2,5
18	13	13	11,5	17,5
19	23	23	17,5	28,5
20	6	6	2,5	8,5
21	7	7	3,5	9,5
22	10	10	5,5	11,5
23	15	15	7,5	19,5
24	16	16	9,5	18,5
25	18	18	10,5	19,5
26	8	8	12	22
27	7	9	16	24
28	11	11	14	9
29	12	12	17	16
30	14	14	8	18

Рис.1

Решение:

Рассмотрим равновесие стержня ABDC вместе с диском. На эту систему тел действуют силы P, S; реакция в подпятнике с составляющими ХА, YA, ZA; реакция в подшипнике с составляющими ХB и YB, которые предполагаем направленными в положительные стороны осей координат.

Составим шесть условий равновесия для сил. Для проекций сил на оси координат имеем:

(a)

При определении проекций силы Р на оси координат предварительно раскладываем ее на две перпендикулярные составляющие, одна из которых параллельна оси Оу и имеет проекцию на эту ось Ру=Pcosα. Перпендикулярная составляющая расположится в плоскости Axz и будет иметь величину проекции на эту плоскость

Р_хz = Р sin α.

Силу Рхz как вектор проецируем на оси координат Ах и Az. Имеем

Р_х= -P_xzsinβ= -Psinαsinβ; P_z =P_xzcos β = Psinαcosβ.

Для моментов сил относительно осей координат получаем:

(б)

При вычислении момента силы относительно оси координат, согласно определению, проецируем силу на плоскость, перпендикулярную оси, и затем вычисляем момент проекции силы относительно точки пересечения оси с плоскостью. Силы, параллельные оси или ее пересекающие, дают моменты относительно этой оси, равные нулю. При определении момента силы S относительно осей координат раскладываем ее на составляющие, параллель­ные осям координат, вычисляем на основании теоремы Вариньона моменты каждой из составляющих относительно соответствующих осей координат и складываем их алгебраически. Значения составляющих сил равны проекциям этих сил на оси координат и их можно взять из уравнений (а). Аналогично вычисляются моменты силы Р.

Решая систему линейных уравнений (а) и (б) относительно проекций неизвестных сил, можно определить все неизвестные силы.

Подставляя в уравнения (а) и (б) заданные значения сил, расстояний и углов, получим:

Решая эту систему уравнений, имеем:

S=30 кН; Х_B =32,7 кН; Х_A = -2,7 кН; Yв = 0,5кН; Y_A =15,5кН; Z_A=8,7кН.

Задачи на тему: “Кинематика”