
- •2 Семестр. Фнп. Кратные интегралы. Теория поля
- •1. Метрические пространства. Открытые и замкнутые множества. Понятие области
- •2. Функции многих переменных. Предел и непрерывность функций многих переменных. Частные производные и их геометрический смысл
- •3. Дифференцируемость функций многих переменных, связь с частными производными. Полный дифференциал. Достаточное условие дифференцируемости
- •1. Теоремы о непрерывности и дифференцируемости сложной функции
- •2. Неявная функция и её дифференцирование
- •3. Частные производные и дифференциалы высших порядков. Равенство смешанных производных
- •4. Скалярное поле. Производная скалярного поля по направлению, связь с градиентом
- •1. Касательная плоскость и нормаль к поверхности
- •2. Локальный экстремум функции нескольких переменных, необходимое условие экстремума. Достаточные условия существования экстремума
- •3. Наибольшее и наименьшее значения функции
- •4. Условный экстремум. Метод множителей Лагранжа
- •Лекция 4. Двойные и тройные интегралы, их определения, свойства и вычисление путем сведения к повторным интегралам. Вычисление площадей плоских фигур и объёмов тел
- •1. Двойной интеграл, его свойства и вычисление
- •2. Тройной интеграл, его свойства и вычисление
- •3. Приложения кратных интегралов
- •1 . Криволинейные координаты на плоскости
- •2. Двойной интеграл в полярных координатах
- •3. Криволинейные координаты в пространстве. Тройной интеграл в цилиндрических и сферических координатах
- •4. Площадь поверхности
- •1.Поверхностный интеграл
- •2. Векторное поле. Векторные линии векторные трубки. Ориентируемые поверхности и поток векторного поля через поверхность
- •3. Дивергенция, её физический смысл и свойства. Формула Остроградского-Гаусса
- •1. Инвариантное определение дивергенции и её физический смысл
- •2. Соленоидальное поле и его свойства
- •3. Ориентируемые кривые. Криволинейные интегралы первого и второго рода, их свойства и вычисление
- •4. Сведение криволинейного интеграла второго рода по замкнутому контуру к двойному интегралу. Формула Грина
- •5. Циркуляция и ротор векторного поля, их вычисление и физический смысл. Формула Стокса
4. Сведение криволинейного интеграла второго рода по замкнутому контуру к двойному интегралу. Формула Грина
Имеет место следующее утверждение.
Теорема
Грина. Пусть
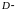 односвязная
ограниченная область в
односвязная
ограниченная область в
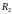 с кусочно гладкой границей
с кусочно гладкой границей
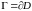 (в этом случае
(в этом случае
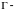 замкнутый
контур) и пусть функции
замкнутый
контур) и пусть функции
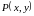 и
и
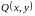 и их частные производные
и их частные производные
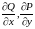 непрерывны в
непрерывны в
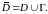 Тогда имеет место равенство
Тогда имеет место равенство
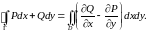
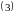
Здесь контур
обходится так, чтобы область
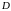 оставалась слева от наблюдателя, идущему
по этому контуру.
оставалась слева от наблюдателя, идущему
по этому контуру.
Доказательство
проведем
для области
правильной
в направлениях осей
 и
и
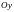 с гладкой границей
с гладкой границей
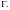 В этом случае область
может быть описана двумя способами:
В этом случае область
может быть описана двумя способами:
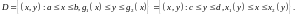
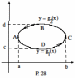
Поле
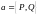 можно записать в виде
можно записать в виде
 В силу линейности интеграла получаем,
что
В силу линейности интеграла получаем,
что
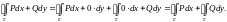
Преобразуем каждый из стоящих здесь интегралов:
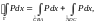
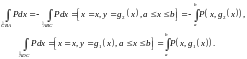
Следовательно,
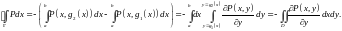
Аналогично
показываем, что
 поэтому (согласно (4)) верно равенство
(3).
поэтому (согласно (4)) верно равенство
(3).
Теорема доказана.
Пример
1 (Кузнецов
Л.А. Типовые расчеты).
Найти работу
силы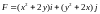 при перемещении вдоль отрезка
при перемещении вдоль отрезка от точки
от точки
 к
точке
к
точке
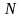 .
.
Р ешение.
Вычисления
разобьём на две части: сначала вычис-лим
работу от точки
до точки
ешение.
Вычисления
разобьём на две части: сначала вычис-лим
работу от точки
до точки
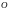 ,
затем – от точки
до точки
,
затем – от точки
до точки
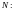
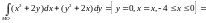
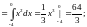
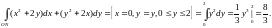
Значит,

 Пример 2.
Вычислить
криволинейный интеграл
Пример 2.
Вычислить
криволинейный интеграл
 если
если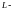 контур
треугольника
с вершинами
контур
треугольника
с вершинами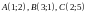 пробегаемый против часовой стрелки.
пробегаемый против часовой стрелки.
Решение. Так как контур интегрирования замкнут, то можно воспользоваться формулой Грина:
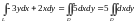 .
.
Интеграл
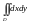 численно равен площади
численно равен площади
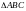 .
Так как
.
Так как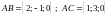 ,
то
,
то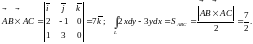
5. Циркуляция и ротор векторного поля, их вычисление и физический смысл. Формула Стокса
Циркуляцией
векторного поля
вдоль замкнутого контура
 называется криволинейный интеграл
называется криволинейный интеграл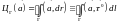 (здесь
(здесь
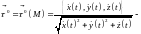 единичный вектор касательной к кривой
в
точке
единичный вектор касательной к кривой
в
точке
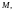 а
сам контур
ориентирован с помощью этого вектора).
а
сам контур
ориентирован с помощью этого вектора).
Так
как циркуляция есть изученный выше
криволинейный интеграл второго рода,
то она обладает всеми свойствами этого
интеграла (линейность, аддитивность,
ориентированность и т.д.). Он имеет тот
же физический смысл: если
сила,
действующая на материальную точку
,
то циркуляция
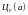 равна работе
силового поля
по перемещению точки
вдоль контура
.
Для вычисления циркуляции поля
можно воспользоваться формулой (2):
равна работе
силового поля
по перемещению точки
вдоль контура
.
Для вычисления циркуляции поля
можно воспользоваться формулой (2):
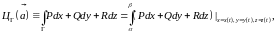
где
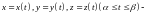 параметрические уравнения контура
,
причем функ-
параметрические уравнения контура
,
причем функ-
ц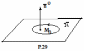 ии
ии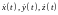 непрерывны на отрезке
и
непрерывны на отрезке
и
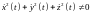 на этом отрезке, а ориентация (обход)
контура
соответствует
возрастанию параметра
на этом отрезке, а ориентация (обход)
контура
соответствует
возрастанию параметра
С циркуляцией
поля
тесно связано понятие ротора этого
поля, к описанию которого мы переходим.
Пусть
фиксированная
точка области
в которой действует поле
,
и пусть
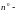 произвольное
фиксированное направление в этой точке.
Проведем плоскость
произвольное
фиксированное направление в этой точке.
Проведем плоскость
 через точку
,
ортогональную вектору
,
и окружим эту точку кусочно гладким
контуром
,
лежащим в плоскости
.
Пусть
через точку
,
ортогональную вектору
,
и окружим эту точку кусочно гладким
контуром
,
лежащим в плоскости
.
Пусть
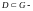 область, окружённая контуром
.
Будем говорить, что направление
и направление на контуре
согласованы,
если обход контура
виден из конца вектора
совершающимся против
часовой стрелки.
Итак, пусть направления
и контура
согласованы
и пусть
площадь
области
область, окружённая контуром
.
Будем говорить, что направление
и направление на контуре
согласованы,
если обход контура
виден из конца вектора
совершающимся против
часовой стрелки.
Итак, пусть направления
и контура
согласованы
и пусть
площадь
области
Определение 3. Предел
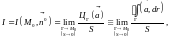
когда контур стягивается в точку называется плотностью циркуляции поля в точке в направлении вектора .
Определение
4. Ротором
(или вихрем) векторного поля
в
точке
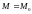 называется такой вектор
проекция
которого на любое направление
совпадает с плотностью циркуляции
поля
в
точке
в направлении вектора
, т.е.
называется такой вектор
проекция
которого на любое направление
совпадает с плотностью циркуляции
поля
в
точке
в направлении вектора
, т.е.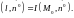 Обозначение:
Обозначение:
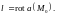
Это определение ротора не зависит от выбора системы координат, т.е. является инвариантным. Используя формулу Грина, нетрудно доказать следующее утверждение.
Теорема
3 (о
вычислении ротора в декартовой системе
координат).
Пусть
векторное поле
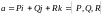 задано
в
декартовой системе координат и пусть
это поле непрерывно дифференцируемо
в точке
Тогда
задано
в
декартовой системе координат и пусть
это поле непрерывно дифференцируемо
в точке
Тогда
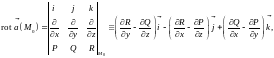
где все частные производные вычисляются в точке (здесь символический определитель разложен по первой строке).
Опишем теперь
связь между циркуляцией и ротором.
Сначала отметим, что область
называется поверхностно
односвязной,
если на любой замкнутый контур
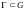 можно натянуть непрерывную поверхность
не
выходя из области
Например, шар –
поверхностно односвязная область, а
шар
с тоннелем – не является таковой, так
как на любой замкнутый контур, охватывающий
тоннель, нельзя натянуть непрерывную
поверхность, не выходя из
можно натянуть непрерывную поверхность
не
выходя из области
Например, шар –
поверхностно односвязная область, а
шар
с тоннелем – не является таковой, так
как на любой замкнутый контур, охватывающий
тоннель, нельзя натянуть непрерывную
поверхность, не выходя из
 Теорема
Стокса. Пусть
поверхностно
односвязная область и пусть векторное
поле
Теорема
Стокса. Пусть
поверхностно
односвязная область и пусть векторное
поле
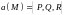 непрерывно дифференцируемо в
Тогда
каков бы ни был кусочно гладкий замкнутый
контур
и какова бы ни была кусочно гладкая
поверхность
натянутая на контур
непрерывно дифференцируемо в
Тогда
каков бы ни был кусочно гладкий замкнутый
контур
и какова бы ни была кусочно гладкая
поверхность
натянутая на контур
 имеет место равенство8
имеет место равенство8
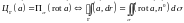 .
.
Здесь
нормаль
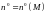 к поверхности
направлена так, что её направление в
каждой точке
согласовано с направлением обхода
контура
к поверхности
направлена так, что её направление в
каждой точке
согласовано с направлением обхода
контура
Пример
3 (Кузнецов
Л.А. Типовые расчеты).
Найти модуль циркуляции векторного
поля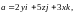 вдоль контура
вдоль контура
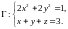
Решение.
Поскольку контур
замкнутый (окружность, находящаяся в
плоскости
 ),
то можно воспользоваться формулой
Стокса (6). В качестве поверхности
натянутой
на контур
,
удобно взять плоскость
.
Так как надо найти модуль циркуляции,
то направление на контуре не имеет
значения, а в качестве вектора
можно взять вектор нормали к плоскости:
),
то можно воспользоваться формулой
Стокса (6). В качестве поверхности
натянутой
на контур
,
удобно взять плоскость
.
Так как надо найти модуль циркуляции,
то направление на контуре не имеет
значения, а в качестве вектора
можно взять вектор нормали к плоскости:
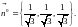 Вычислим ротор:
Вычислим ротор:
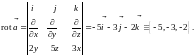
По формуле Стокса имеем

Здесь
проекция
поверхности
на плоскость
т.е.
круг радиуса
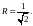 Площадь этого круга равна
Площадь этого круга равна
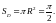 Значит,
Значит,
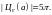
1 Далее значок “def” и некоторые скобки в определении предела будем опускать.
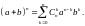
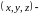
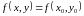
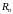
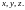
2 По определению дифференциалы независимых переменных совпадают с их приращениями.
3 Здесь используется формула бинома Ньютона:
4 Здесь произвольная (текущая) точка нормали.
5 Заметим, что если равенство достигается только в точке , то соответствующий экстремум называется строгим экстремумом.
6 Замкнутое ограниченное множество в называется компактом.
7 Число связей должно быть меньше числа независимых переменных
8 Формулу (6) называют формулой Стокса.
