1. Знакочередующиеся ряды. Теорема Лейбница
Ряд
называется знакочередующимся,
если все его члены
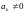и чередуются знаками, т.е.
Таким образом, знакочередующийся ряд имеет вид
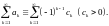
Теорема
Лейбница. Пусть
в знакочередующемся ряде (1) общий член
стремится к нулю, т.е.
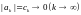и последовательность
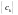строго убывает, т.е.
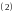
Тогда ряд (1)
сходится и его сумма
и
й
остаток
удовлетворяют неравенствам
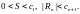При этом
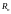имеет знак
(
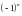знак первого отброшен-
ного члена
).
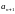Доказательство.
Запишем частичную сумму
с чётными номерами и расставим в ней
скобки следующим образом:
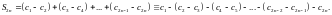
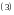
Так как имеют
место неравенства (2), то из первого
представления
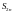в виде суммы скобок получаем, что
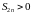и
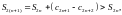т.е. последовательность
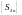строго возрастает. Из второго представления
(3) и неравенств
(2) выводим неравенства
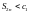
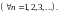Таким образом, последовательность
строго возрастает и ограничена сверху,
поэтому (см. свойство 7 предыдущей
лекции) она имеет конечный предел
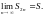Так как
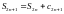и так как
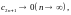то
существует предел
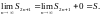Значит, существует предел всей
последовательности
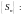
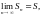и поэтому ряд (1) сходится к сумме
Аналогично
показываем, что последовательность
частичных сумм
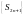ряда (1) с нечетными номерами:
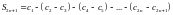
строго убывает.
В следствие строго убывания
последовательности
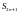и строго возрастания последовательности
и стремления их к пределу
будут выполняться неравенства
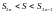
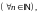поэтому (в частности при
)
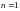будем иметь
Первая часть
теоремы доказана. Применив её к
знакочередующемуся ряду
легко докажем и вторую часть теоремы,
т.е. неравенство
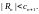Теорема полностью доказана.
Пример 1.
Вычислить
сумму ряда
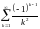с точностью до 0,01.
Решение.
Данный ряд
сходится абсолютно, так его модульный
ряд
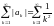является обобщенным гармоническим
рядом с показателем
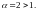В то же время данный ряд является
знакочередующимся. Для него выполнены
все условия теоремы Лейбница, поэтому
его остаток
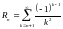может быть оценен следующим образом:
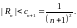Мы хотим, чтобы
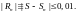Для этого надо взять такое
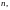чтобы
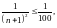откуда выводим, что
Значит, частичная сумма
будет решением нашей задачи.
2.Функциональные ряды. Поточечная и равномерная сходимость. Теорема Вейерштрасса
Пусть
дана некоторая последовательность
функций
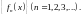Областью
опреде-
ления этой
последовательности называется множество
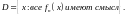По
этой последовательности можно построить
ряд
.
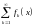Этот ряд называется функциональ-
ным рядом.
Его областью определения называют
множество
функциональной последовательности
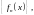по которой он строится. Дадим понятие
поточечной
сходимости
этого ряда.
Определение
2. Говорят,
что ряд
сходится в точке
к сумме
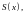если существует конечный предел его
частичным сумм:
.
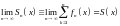Или (на языке “
”): если
Обращаем
внимание на то, что здесь номер
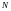зависит не только от
но и от точки
,
в которой рассматривается сходимость
ряда. Если же этот номер не зависит от
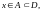то указанный ряд будет сходиться к
сумме
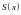равномерно
на множестве
Дадим строгое определение такой
сходимости.
Определение
3. Говорят,
что ряд
сходится к сумме
равномерно
на множестве
,
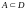если
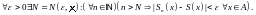
Здесь перечеркнутое
означает, что номер
зависит только от
и не зависит от точек
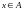(номер
обслуживает все
одновременно!).
Отметим следующие очевидные свойства равномерно сходящихся рядов.
3. Если ряд
сходится равномерно к сумме
на множестве
,
то он сходится равномерно и на любом
подмножестве
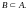
4. Если ряды
и
сходятся равномерно на множестве
(
к суммам
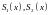соответственно), то ряд
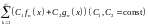также равномерно сходится на множестве
(к сумме
).
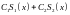5 (критерий
Коши равномерной сходимости ряда).
Для того чтобы ряд
сходится равномерно на множестве
,
необходимо и достаточно, чтобы
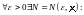
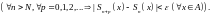
Введем еще
некоторые понятия. Множество всех
точек
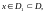в которых ряд
сходится, называется множеством
его поточечной сходимости, а
множество всех точек
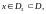в
которых сходится модульный ряд
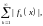называется множеством
его абсолютной сходимости. Ясно,
что множество
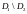будет множеством
условной сходимости
ряда
.
Обычно сначала исследуют поточечную сходимость, для чего составляют модульный ряд
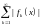и применяют к
нему сформулированные ранее признаки
сходимости для знакоположительных
числовых рядов (признаки сравнения,
Даламбера, Коши и интегральный признак),
фиксируя при этом мысленно аргумент
Затем
находят область условной сходимости
(здесь обычно применяется признак
Лейбница) и, наконец, область равномерной
сходимости функционального ряда. При
этом используют следующее утверждение.
Критерий
Вейерштрасса
(равномерной сходимости ряда). Пусть
для функционального ряда
найдется
числовой ряд
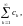обладающий
свойствами:
а)
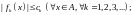б) ряд
сходится.
Тогда ряд сходится равномерно на множестве
(числовой ряд обладающий свойствами а) и б) называется мажорирующим рядом для ряда ).
Доказательство вытекает из неравенства
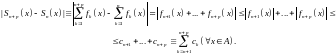
Действительно,
для числового ряда
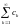справедлив признак Коши сходимости,
значит,
(
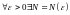не зависит от
так
как ряд
числовой):
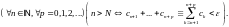
Но тогда из (4) вытекает высказывание
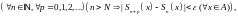
т.е. для функционального ряда справедлив критерий 5 равномерной сходимости. Следовательно, этот ряд сходится равномерно на множестве Теорема доказана.
Например,
применяя критерий Вейерштрасса к ряду
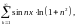будем иметь
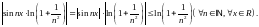
Так как
то
ряд
сходится, а значит,
исходный ряд сходится равномерно на
всей оси
Рассмотрим еще один пример.
Пример 2.
Найти область сходимости функционального
ряда
.
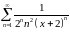Решение.
Общий член ряда 
.
Тогда последующий член ряда получается
заменой 
на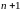 
:
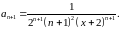Вычислим предел
.
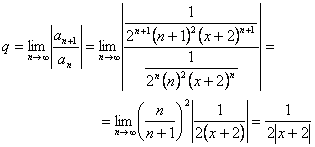По признаку Даламбера ряд
сходится, если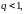 
т. е. должно выполняться неравен-
ство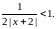 
Преобразуя последнее неравенство к
виду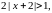 
получаем, что в
области
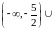
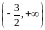ряд сходится абсолютно. Исследуем
сходимость ряда на концах интервала.
При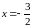 
ряд имеет вид 
.
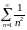Это сходящийся ряд обобщенный
гармонический ряд (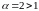
).
При 
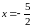ряд имеет вид 
.
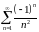Это знакочередующийся ряд, который
сходится абсолютно, так как ряд,
составленный из модулей сходится.
Таким образом, область сходи-
мости
исходного функционального ряда
будет такой:
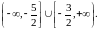Заметим, что нашу задачу можно было бы
решить, сделав в исходном ряде замену
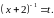Тогда получим так называемый степенной
ряд
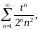который будет сходиться в области
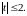На следующей лекции будет показано,
что этот ряд будет сходиться равномерно
на любом отрезке
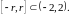
Лекция 3. Свойства равномерно сходящихся рядов: непрерывность суммы, её дифференцируемость и интегрируемость. Степенные ряды. Теорема Абеля, радиус и интервал сходимости. Непрерывность суммы степенного ряда. Дифференцирование и интегрирование степенного ряда. Ряды Тейлора. Условия разложимости функции в ряд Тейлора
Напомним сначала определение равномерной сходимости функционального ряда.
Определение 1. Говорят, что ряд сходится к сумме равномерно на множестве , если
Здесь перечеркнутое означает, что номер зависит только от и не зависит от точек (номер обслуживает все одновременно!).