- •2 Семестр. Ряды
- •1. Предел последовательности. Арифметические действия над пределами. Предел монотонной последовательности
- •2. Числовые ряды, их сходимость и расходимость. Действия со сходящимися рядами. Признак Коши сходимости. Необходимое условие сходимости ряда. Признаки сходимости для знакоположительных рядов
- •3. Знакоположительные ряды. Теоремы с равнения. Признаки сходимости Даламбера и Коши, интегральный признак
- •1. Знакочередующиеся ряды. Теорема Лейбница
- •2.Функциональные ряды. Поточечная и равномерная сходимость. Теорема Вейерштрасса
- •1.Свойства равномерно сходящихся рядов: непрерывность суммы, её дифференцируемость и интегрируемость
- •2.Степенные ряды. Теорема Абеля, радиус и интервал сходимости. Непрерывность суммы степенного ряда. Дифференцирование и интегрирование степенного ряда
- •3.Ряды Тейлора. Условия разложимости функции в ряд Тейлора
3. Знакоположительные ряды. Теоремы с равнения. Признаки сходимости Даламбера и Коши, интегральный признак
Ряд
называется знакоположительным,
если все его члены
 Заметим, что если неравенства
Заметим, что если неравенства
 выполняются, начиная с некоторого
номера
выполняются, начиная с некоторого
номера
 то заменив первые его
то заменив первые его
 членов на произвольные положительные
числа, сделаем указанный ряд
знакоположительным, причем полученный
ряд и исходный ряд будут сходиться или
расходится одновременно.
членов на произвольные положительные
числа, сделаем указанный ряд
знакоположительным, причем полученный
ряд и исходный ряд будут сходиться или
расходится одновременно.
12. Частичные суммы образуют неубывающую последовательность.
Действительно,
так как
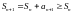 (учесть, что
(учесть, что
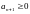 ),
то последовательность
не убывает. Из свойства
7 вытекает
следующее отверждение.
),
то последовательность
не убывает. Из свойства
7 вытекает
следующее отверждение.
Общий признак сходимости знакоположительных рядов. Если последовательность частичных сумм знакоположительного ряда ограничена сверху, то это ряд сходится.
Замечание 2. Так как последовательность частичных сумм знакоположитель-
ного ряда не
убывает, то при расходимости
соответствующего ей ряда предел
 (почему?). В этом случае считают, что
сумма ряда
(почему?). В этом случае считают, что
сумма ряда

Теорема сравнения I. Пусть для рядов

выполнены неравенства
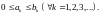
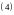
Тогда из сходимости ряда (3) вытекает сходимость ряда (2), а из расходимости ряда (2) вытекает расходимость ряда (3).
Доказательство.
Пусть сходится ряд (3). Тогда
последовательность
 его час-
его час-
тичных сумм
ограничена, т.е. существует постоянная
 такая, что
такая, что
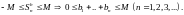
Учитывая
неравенства (4), будем иметь
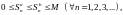 т.е. последователь-
т.е. последователь-
ность
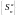 ряда (2) ограничена сверху. Отсюда (по
общему признаку сходимости) следует,
что ряд (2) сходится. Если теперь ряд (2)
расходится, то
ряда (2) ограничена сверху. Отсюда (по
общему признаку сходимости) следует,
что ряд (2) сходится. Если теперь ряд (2)
расходится, то
 (так как последовательность
неубывающая).
Переходя в неравенстве
(так как последовательность
неубывающая).
Переходя в неравенстве
 к пределу при
к пределу при
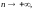 получаем, что и
получаем, что и
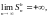 т.е. ряд (3) также расходится. Теорема
доказана.
т.е. ряд (3) также расходится. Теорема
доказана.
Теорема сравнения II. Пусть для знакоположительных рядов
выполнены условия:
1)
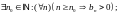 2) существует предел
2) существует предел

Тогда ряды (2) и (3) одновременно сходятся или одновременно расходятся.
Замечание 3.
Обычно эта
теорема применяется в случае, когда
последовательности
 и
и
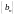 эквивалентны
эквивалентны
 В этом случае
В этом случае
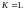 При этом в качестве ряда (3) берут
обобщенный гармонический ряд
При этом в качестве ряда (3) берут
обобщенный гармонический ряд
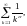 а для описания поведения общего члена
ряда (2) пользуются таблицей 1 эквивалентных
бесконечных малых. Ниже будет показано,
что обобщенный
гармонический
ряд сходится,
если
а для описания поведения общего члена
ряда (2) пользуются таблицей 1 эквивалентных
бесконечных малых. Ниже будет показано,
что обобщенный
гармонический
ряд сходится,
если
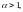 и расходится при
и расходится при
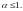
Пример 1.
Исследовать на сходимость ряд

Решение. Имеем
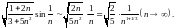 Постоянная
Постоянная
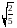 не влияет на
сходимость ряда (см. утверждение 11),
поэтому ее можно не учитывать. Ряд
не влияет на
сходимость ряда (см. утверждение 11),
поэтому ее можно не учитывать. Ряд
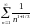 сходится, так как
сходится, так как
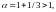 а значит, и исходный ряд также сходится.
а значит, и исходный ряд также сходится.
Сформулируем ещё три признака, которые используются при исследовании сходимости рядов.
Признак
Даламбера. Пусть
знакоположительный ряд
таков, что
 и пусть существует (конечный или
бесконечный) предел
и пусть существует (конечный или
бесконечный) предел
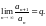 Тогда при
Тогда при
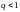 указанный ряд сходится, а при
указанный ряд сходится, а при
 он расходится. При
он расходится. При
 ничего о сходимости данного ряда сказать
нельзя; нужны дополнительные исследования.
ничего о сходимости данного ряда сказать
нельзя; нужны дополнительные исследования.
Признак Коши
(радикальный). Пусть
знакоположительный ряд
таков, что существует
(конечный
или бесконечный) предел
 Тогда при
указанный ряд сходится, а при
он расходится. При
ничего о сходимости данного ряда сказать
нельзя; нужны дополнительные исследования.
Тогда при
указанный ряд сходится, а при
он расходится. При
ничего о сходимости данного ряда сказать
нельзя; нужны дополнительные исследования.
Интегральный
признак сходимости Коши. Пусть
для ряда
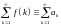 выполнены следующие условия:
выполнены следующие условия:
1) функция
 неотрицательна и непрерывна при
неотрицательна и непрерывна при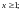
2) функция
не
возрастает на промежутке
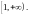
Тогда ряд
 и интеграл
и интеграл
 одновременно
сходятся или одновременно расходятся.
При этом
имеет место следующая оценка остатка
одновременно
сходятся или одновременно расходятся.
При этом
имеет место следующая оценка остатка


Используем,
например, этот признак для исследования
сходимости обобщенного гармонического
ряда
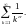 Составим функцию
Составим функцию
 (заменив в
(заменив в
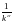 натуральное число
натуральное число
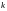 на
на
 ).
Функция
удовлетворяет условиям 1) и 2) интегрального
признака Коши, поэтому ряд
).
Функция
удовлетворяет условиям 1) и 2) интегрального
признака Коши, поэтому ряд
 и несобственный интеграл
и несобственный интеграл
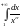 сходятся или расходятся одновременно.
Из предыдущих лекций известно, то
эталонный интеграл
сходится при
сходятся или расходятся одновременно.
Из предыдущих лекций известно, то
эталонный интеграл
сходится при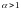 и расходится при
Значит, и обобщенный
гармонический
ряд сходится,
если
и расходится при
и расходится при
Значит, и обобщенный
гармонический
ряд сходится,
если
и расходится при
Лекция 2. Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимость. Теорема Лейбница и оценка остаточного члена знакочередующегося ряда.
Свойства абсолютно сходящихся рядов. Функциональные ряды. Поточечная и равномерная сходимость. Теорема Вейерштрасса
Если ряд
содержит
бесконечное число положительных и
бесконечное число отрицательных членов
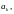 то
этот ряд называется знакопеременным
рядом.
то
этот ряд называется знакопеременным
рядом.
Определение
1. Ряд
называется
абсолютно
сходящимся,
если сходится его “модульный” ряд
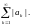 Если же ряд
сходится,
а его “модульный”2
ряд
Если же ряд
сходится,
а его “модульный”2
ряд
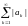 расходится,
то ряд
называется условно
сходящимся.
расходится,
то ряд
называется условно
сходящимся.
Теорема 1 (об обычной сходимости абсолютно сходящегося ряда). Если ряд , то
сходится и ряд
Доказательство.
Так как
сходится ряд
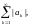 то
для него справедлив признак Коши
сходимости:
то
для него справедлив признак Коши
сходимости:

Тогда для ряда
и указанного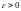 имеем
имеем
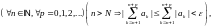
т.е. для ряда также выполняется признак Коши сходимости, поэтому он сходится. Теорема доказана.
Например, ряд
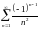 абсолютно сходится, так как сходится
его модульный ряд
абсолютно сходится, так как сходится
его модульный ряд
 В качестве условно
сходящегося ряда можно указать ряд
В качестве условно
сходящегося ряда можно указать ряд
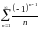 (его сходимость вытекает из теоремы
Лейбница, сформулированной ниже). Его
модульный ряд
(его сходимость вытекает из теоремы
Лейбница, сформулированной ниже). Его
модульный ряд
 расходится.
расходится.
С абсолютно сходящимися рядами можно обращаться так же, как и с конечными сумма-
ми, а именно: имеют место следующие свойства абсолютно сходящихся рядов.
1. Если ряд сходится абсолютно, то в нем можно произвольным образом перестав-
лять слагаемые; при этом вновь полученный ряд будет также сходиться абсолютно к той же сумме, что и исходный ряд.
2. Если ряд сходится абсолютно, то в нем можно произвольным образом группировать члены, заключая их в скобки; при этом ряд, полученный из просуммированных членов в скобках, будет также абсолютно сходиться к той же сумме, что и исходный ряд.
Условно сходящиеся ряды такими свойствами не обладают.
Теорема Римана.
Если ряд
сходится
условно, то каково бы ни было наперед
задан-ное число
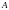 (
может быть ра́вным
(
может быть ра́вным
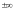 ),
можно так переставить члены этого ряда,
что
),
можно так переставить члены этого ряда,
что
вновь
полученный ряд будет сходиться к числу