- •2 Семестр. Ряды
- •1. Предел последовательности. Арифметические действия над пределами. Предел монотонной последовательности
- •2. Числовые ряды, их сходимость и расходимость. Действия со сходящимися рядами. Признак Коши сходимости. Необходимое условие сходимости ряда. Признаки сходимости для знакоположительных рядов
- •3. Знакоположительные ряды. Теоремы с равнения. Признаки сходимости Даламбера и Коши, интегральный признак
- •1. Знакочередующиеся ряды. Теорема Лейбница
- •2.Функциональные ряды. Поточечная и равномерная сходимость. Теорема Вейерштрасса
- •1.Свойства равномерно сходящихся рядов: непрерывность суммы, её дифференцируемость и интегрируемость
- •2.Степенные ряды. Теорема Абеля, радиус и интервал сходимости. Непрерывность суммы степенного ряда. Дифференцирование и интегрирование степенного ряда
- •3.Ряды Тейлора. Условия разложимости функции в ряд Тейлора
2 Семестр. Ряды
В каждой лекции все формулы, определения и теоремы нумеруются так же, как и в предыдущей лекции, с цифры 1 (т.е. нумерация не продолжается от лекции к лекции). Это удобно при чтении лекций.
Лекция 1. Последовательность и ее предел. Теоремы о пределах. Предел монотонной последовательности. Числовые ряды, их сходимость и расходимость. Действия со сходящимися рядами. Признак Коши сходимости рядов. Необходимый признак сходимости ряда. Знакоположительные ряды. Признаки сравнения, Даламбера и Коши
На предыдущих лекциях подробно изучались функции непрерывного аргумента, их пределы и свойства пределов. В теории рядов фундаментальную роль играют последовательности (т.е. функции дискретного аргумента) и их пределы. Перейдем к изучению соответствующего теоретического материала.
1. Предел последовательности. Арифметические действия над пределами. Предел монотонной последовательности
Последовательностью
называется функция
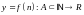 натурального аргумен-
натурального аргумен-
та. При этом
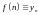 называется общим
членом, а
множество
называется общим
членом, а
множество
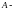 областью определения последовательности
областью определения последовательности
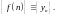
Например,
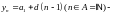 последовательность,
называемая арифметической прогрессией
(
последовательность,
называемая арифметической прогрессией
(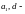 постоянные,
не зависяшие от
постоянные,
не зависяшие от ).
Другой пример:
).
Другой пример:
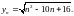 Здесь областью определения является
множество
Здесь областью определения является
множество
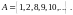
Определение 1.
Число
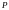 называется пределом последовательности
называется пределом последовательности
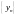 при
при
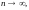 ес-
ес-
ли
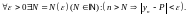 1
При этом пишут
1
При этом пишут
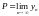 и если этот предел существует и конечен,
то говорят, что последовательность
сходится;
в против-
и если этот предел существует и конечен,
то говорят, что последовательность
сходится;
в против-
ном случае она называется расходящейся последовательностью.
Перечислим основные свойства предела последовательности.
1. Если предел существует, то он единственный.
2. Если в
последовательности
отбросить
любое
конечное
число членов или заменить их на любые
другие числа, то новая последовательность
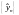 и старая последовательность
будут одновременно расходиться или
сходиться (к одному и тому же пределу
).
и старая последовательность
будут одновременно расходиться или
сходиться (к одному и тому же пределу
).
Из этого свойства
вытекает, что не умоляя общности, можно
считать, что последовательность
определена
при всех
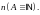
3. Если предел
существует
и конечен, то последовательность
ограничена,
т.е.

4. Если пределы
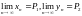 существуют и конечны, то существуют и
пределы
существуют и конечны, то существуют и
пределы
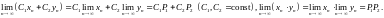 Если
при этом
Если
при этом
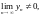 то существует и предел частного
то существует и предел частного
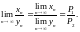
5(критерий
Коши сходимости). Для того чтобы
существовал конечный предел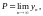 необходимо
и достаточно, чтобы
необходимо
и достаточно, чтобы
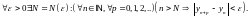
6. При любом
фиксированном
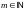 последовательности
и
последовательности
и
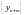 одновременно сходятся или одновременно
расходятся, причем в случае сходимости
они имеют один и тот же предел
одновременно сходятся или одновременно
расходятся, причем в случае сходимости
они имеют один и тот же предел
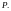
7.Если
последовательность
не убывает (т.е. если )
и ограничена сверху (т.е.
)
и ограничена сверху (т.е.
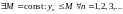 ),
то она имеет конечный предел
),
то она имеет конечный предел
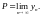 Ана-
Ана-
логичное утверждение верно и для невозрастающей и ограниченной снизу последовательнос-
ти
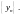
Определение 2.
Последовательность
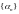 называется бесконечно
малой, если
называется бесконечно
малой, если
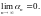 При этом пишут
При этом пишут
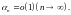 Две
бесконечно малые последовательности
Две
бесконечно малые последовательности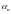 и
и
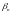 назы-
назы-
ваются
эквивалентными,
если
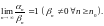 При этом пишут
При этом пишут

8. Для того чтобы
существовал (конечный) предел
необходимо
и достаточно, чтобы имело место
представление
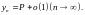
9. Если
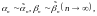 то
то
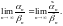
При вычислении пределов последовательности часто используется следующая таблица эквивалентных бесконечно малых.
Таблица 1.
Если
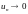 при
при
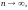 то при
то при
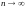 верны
следующие соотношения:
верны
следующие соотношения:
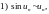
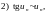
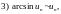

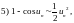

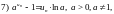
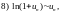
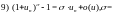
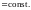 .
.
10)
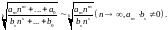
Например, при
вычислении предела
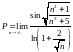 заменяем
заменяем
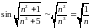 ,
,
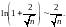 Будем иметь
Будем иметь