Решение
Стационарные точки функции определяются
из системы:
 .
Решение системы
.
Решение системы
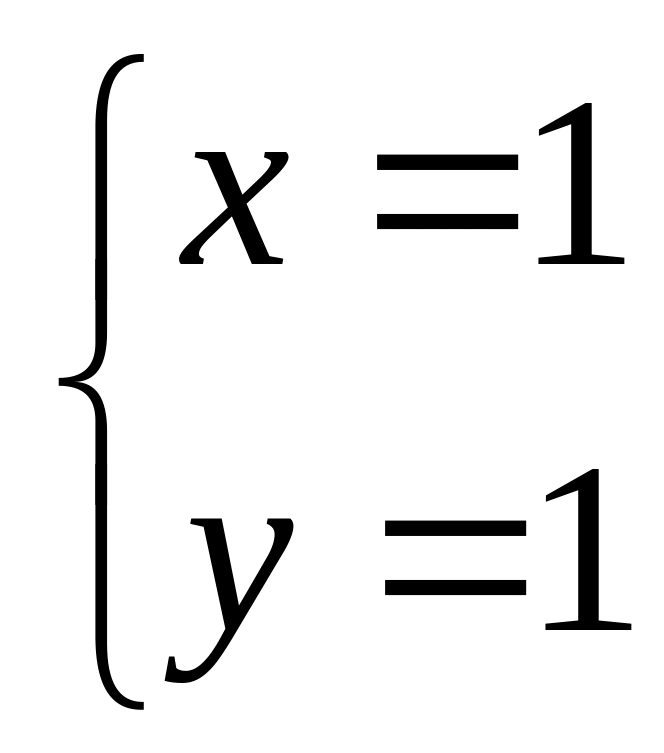 .
Стационарная точка
.
Стационарная точка
 находится внутри заданной области (рис.
5). Значение функции в этой точке равно
находится внутри заданной области (рис.
5). Значение функции в этой точке равно
 .
.
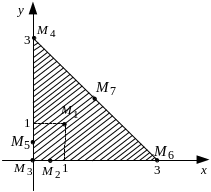
Рис. 5.
Граница области задается уравнениями:
1.
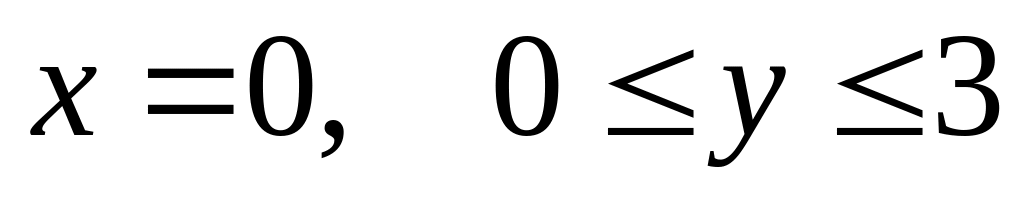 .
На этой части границы
.
На этой части границы
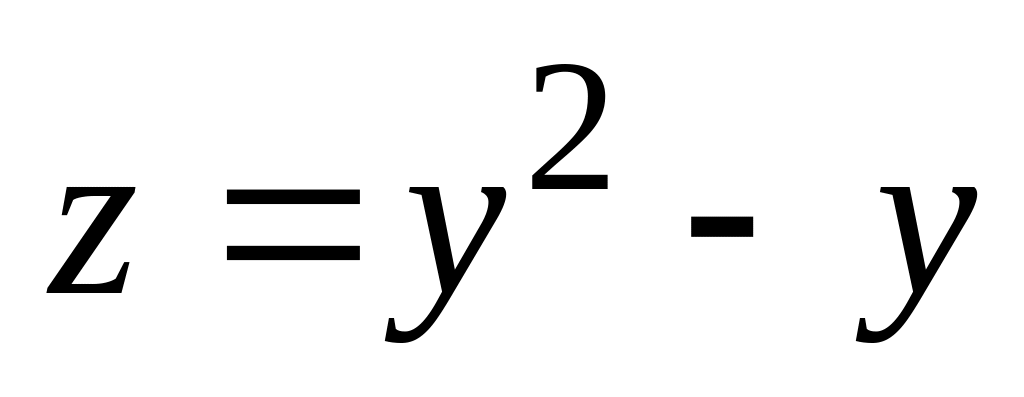 – функция одной переменной. Так как
– функция одной переменной. Так как
 при
при
 ,
то наименьшее и наибольшее значения
функции может быть в точке
,
то наименьшее и наибольшее значения
функции может быть в точке
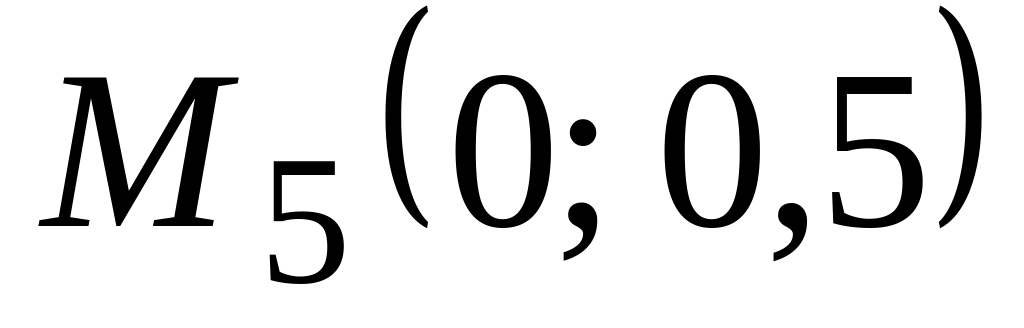 ,
а также в граничных точках
,
а также в граничных точках
 и
и
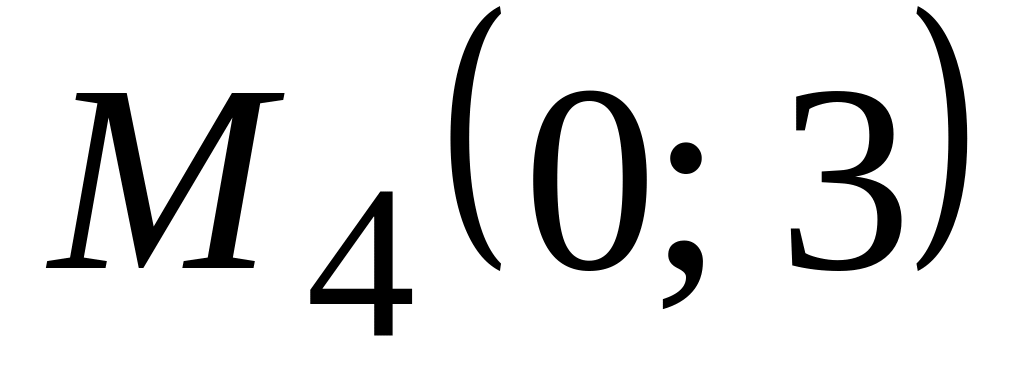 .
Вычислим значения во всех этих точках:
.
Вычислим значения во всех этих точках:
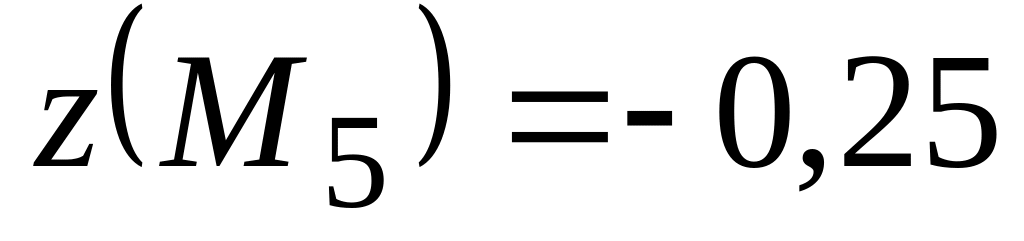 ,
,
 .
.
2.
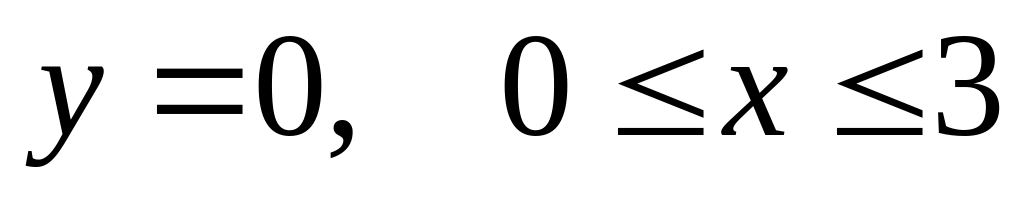 .
На этой части границы
.
На этой части границы
 .
Так как
.
Так как
 при
при
 ,
то наименьшее и наибольшее значения
функции может быть в точке
,
то наименьшее и наибольшее значения
функции может быть в точке
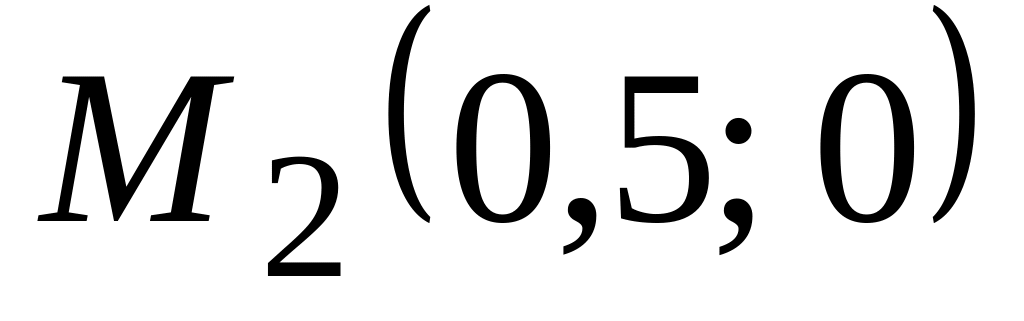 ,
а также в граничных точках
и
,
а также в граничных точках
и
 .
Вычислим значения во всех этих точках:
.
Вычислим значения во всех этих точках:
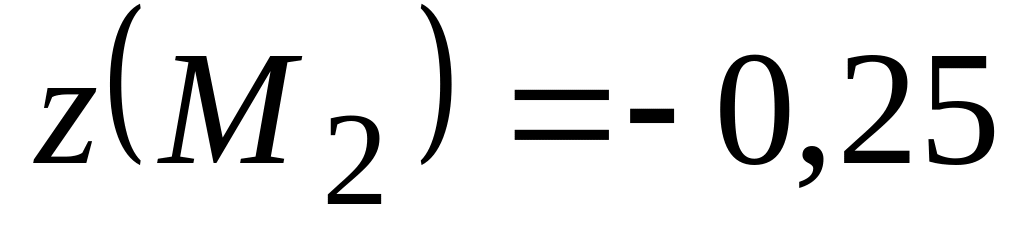 ,
,
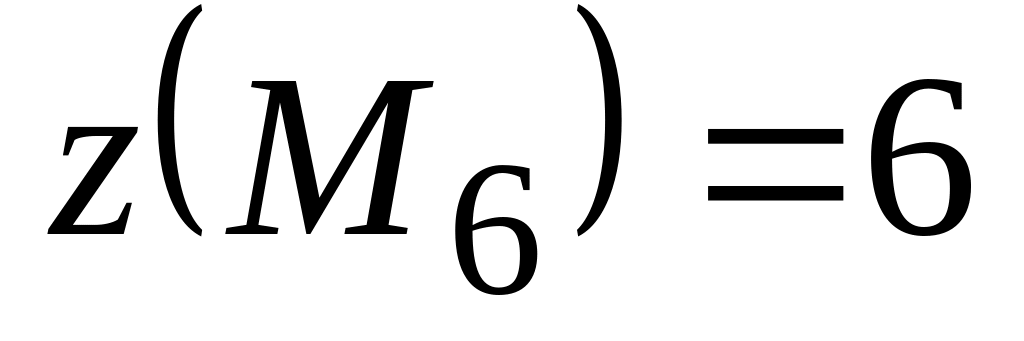 .
.
3.
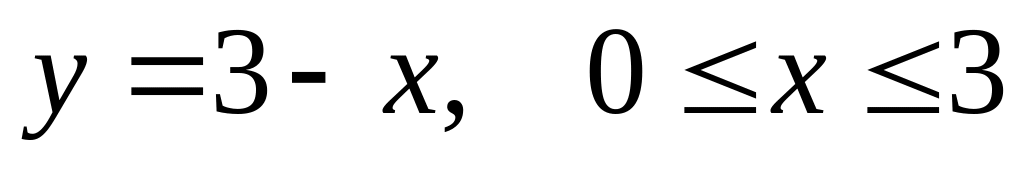 .
На этой части границы
.
На этой части границы
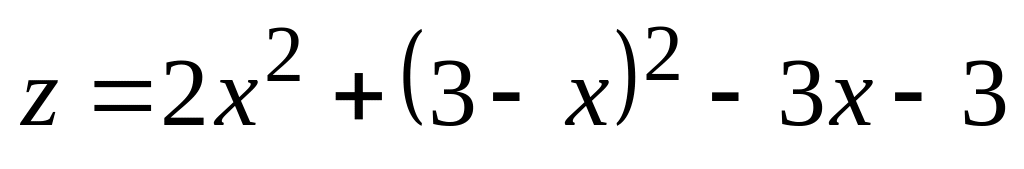 .
Так как
.
Так как
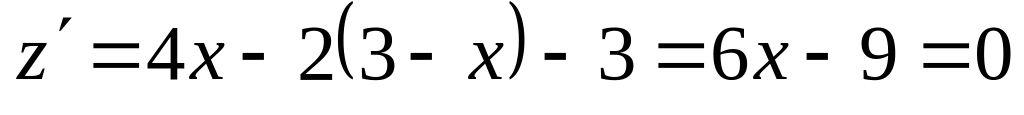 ,
при
,
при
 ,
то наибольшее и наименьшее значение
может быть в точках
,
то наибольшее и наименьшее значение
может быть в точках
 и в граничных точках
и
.
Вычислим
и в граничных точках
и
.
Вычислим
 .
.
Следовательно, наибольшее значение
функции равно
 в точках
и
,
а наименьшее
в точках
и
,
а наименьшее
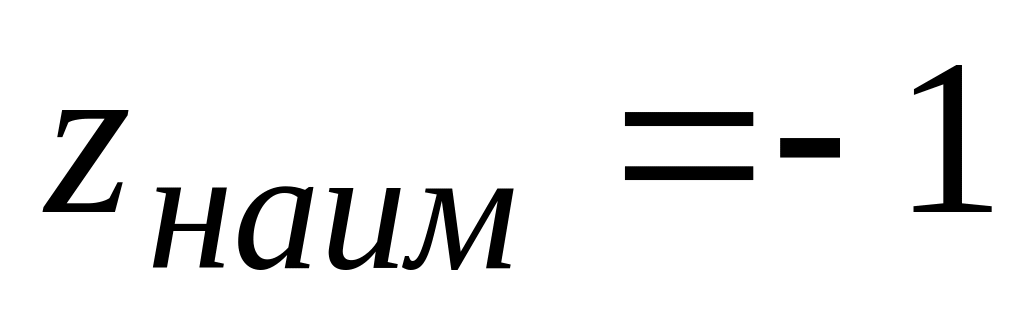 в стационарной точке
.
в стационарной точке
.
32


 .
Решение системы
.
Решение системы
