Теорема 1

Если функция имеет как в точке , так и в некоторой ее окрестности частную производную второго порядка , причем она непрерывна в точке , то в этой точке существует и частная производная , совпадающая с частной производной .

Обобщая теорему на производные более высокого порядка, можно сделать вывод, что при соблюдении указанных условий результат частного дифференцирования не зависит от порядка дифференцирования.

Определение 2

Пусть функция дифференцируема в точке . Тогда в этой точке существует дифференциал . Будем в дальнейшем называть его дифференциалом первого порядка или первым дифференциалом. Дифференциалом второго порядка или вторым дифференциалом функции в точке называется дифференциал от ее первого дифференциала , который обозначается .

Теорема 2

Если задана дифференцируемая функция и - независимые переменные, то имеет место формула

.

Для функции двух переменных , учитывая независимость частных производных от порядка дифференцирования, справедливо:

.

Аналогично определяются дифференциалы более высокого порядка. Дифференциал третьего порядка или третий дифференциал – это дифференциал от второго дифференциала.

Легко показать, что для функции двух переменных формула для третьего дифференциала имеет вид:

.

Формулы для второго дифференциала функции двух переменных удобно записывать в символическом виде:

,

где под записью понимается операция взятия частной производной по переменной , а под записью понимается операция взятия частной производной по переменной .

В общем случае для дифференциала - го порядка функции двух переменных справедлива формула:

.

Замечание 1

Следует помнить, что эти формулы записаны в предположении, что и – независимые переменные

10. Неявная функция. Дифференцируемость неявной функции Определение

Функция называется заданной неявно в окрестности точки , если задано уравнение и если:

;

единственное : .

. Не следует путать вопрос о существовании неявной функции с вопросом получения ее в виде явной зависимости. Следующая теорема дает условия существования, единственности и дифференцируемости неявной функции.

Теорема

Если функция :

непрерывна в окрестности точки ;

имеет в этой окрестности непрерывные частные производные по всем переменным;

;

;

то уравнение задает в окрестности точки однозначную дифференцируемую функцию , для которой справедливо .

Для функции одной переменной , заданной неявной зависимостью , производная в точке вычисляется по формуле:

.

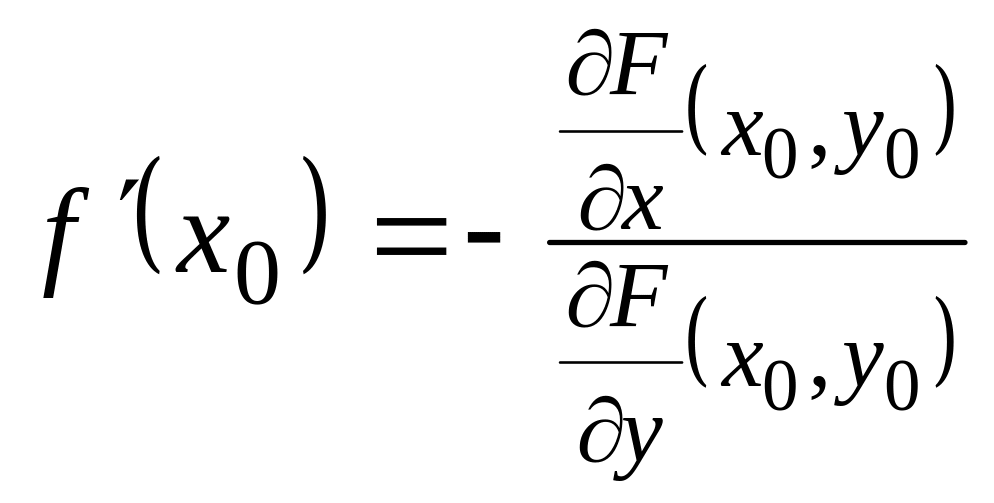Замечание

Для функции формула для вычисления ее производной:

.

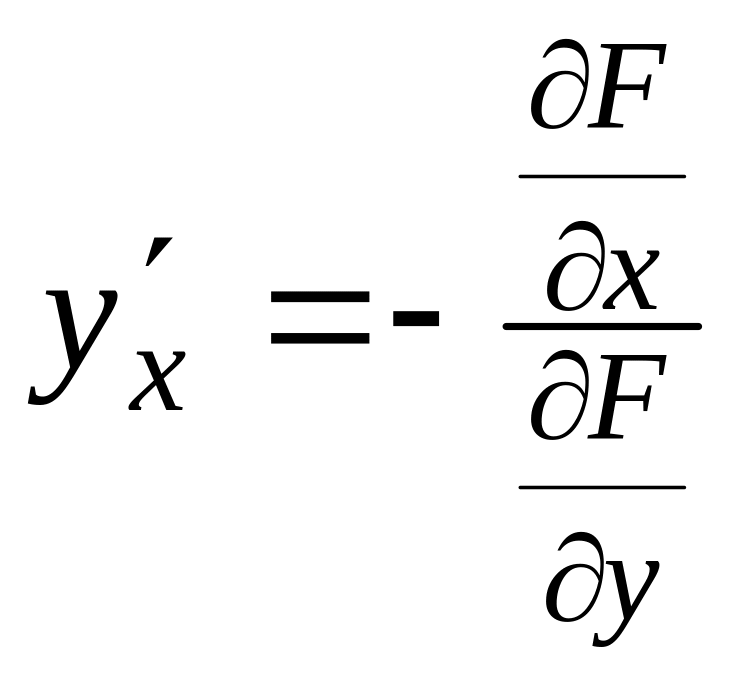Пример

Выясните, в каких точках дифференцируема функция , заданная неявно, и вычислите ее производную, если .

Решение

. Поэтому функция дифференцируема во всех точках, за исключением тех, где . Поскольку , то функция дифференцируема везде, где выполняется условие . Так как , то

.

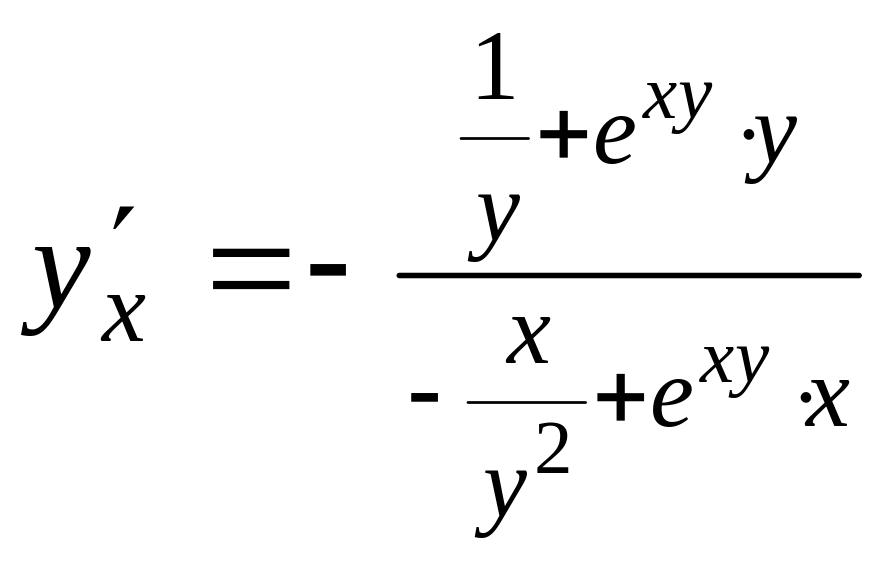11. Экстремум функции двух переменных

Определение 1

Пусть функция определена в области , а – внутренняя точка этой области. Точка называется точкой минимума функции , если

.

Определение 2

Пусть функция определена в области , а - внутренняя точка этой области. Точка называется точкой максимума функции , если

.

Теорема 1

Если функция дифференцируема в окрестности точки и имеет в этой точке экстремум (максимум или минимум), то .

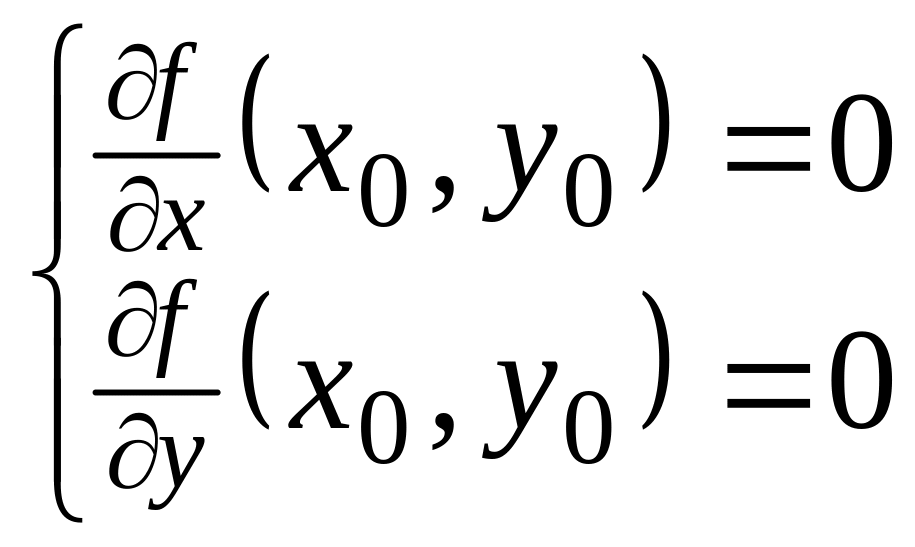Замечание

Доказанная теорема называется необходимым условием экстремума функции двух переменных. Условие равенства нулю частных производных в некоторой точке не является достаточным условием существования экстремума в этой точке.

Следствие

Если хотя бы одна из частных производных или , то в точке нет экстремума.

Значит, экстремум следует искать в тех точках, в которых обе частные производные равны нулю. Так же как и для функции одной переменной экстремум может быть и в точках, где функция не является дифференцируемой. Такие точки в дальнейшем будем называть подозрительными на экстремум или критическими. Среди критических точек особо выделяются стационарные точки.

Определение 3

Точка называется стационарной точкой функции , если дифференцируема в этой точке и , или .

Теорема 2

Если – стационарная точка дважды дифференцируемой функции и если в некоторой окрестности этой точки сохраняет знак, то функция в точке имеет экстремум. При этом если , то этот экстремум минимум. Если , то это максимум.

Замечание

Если меняет знак в окрестности точки , то это еще не означает, что в этой точке нет экстремума.

Пример 1

Функция имеет в точке минимум. Это следует из того, что решением системы

является единственная стационарная точка . Частные производные второго порядка имеют вид:

, , .

Значения частных производных в стационарной точке равны:

, , .

Тогда .

Теорема 3

Если – стационарная точка дважды дифференцируемой функции и если , , , то функция имеет экстремум, если и не имеет экстремума, если . При этом экстремум - максимум, если и минимум, если .

замечание

Если экстремум может быть, а может и не быть. Этот случай требует дополнительных исследований.

Пример 2

Исследовать на экстремум функцию .

Решение

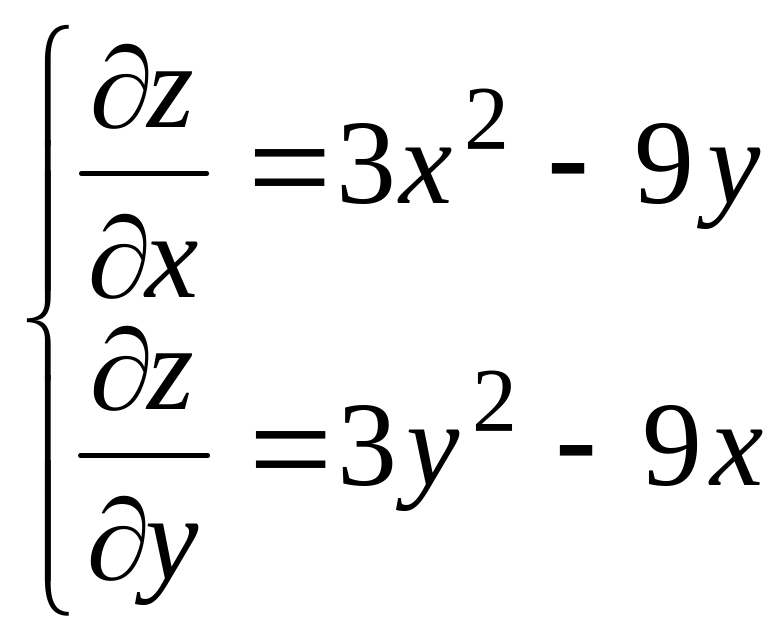, , , , . Системе удовлетворяют две стационарные точки и .

Вычислим частные производные второго порядка , , . Для первой стационарной точки : . Дискриминант . Значит, в этой точке нет экстремума. Для точки : , . Дискриминант , а так как , то это точка минимума.

12. Наименьшее и наибольшее значения функции двух переменных

Теорема

Непрерывная функция , заданная на ограниченном и замкнутом множестве, принимает на этом множестве наибольшее и наименьшее значения.

Наибольшее и наименьшее значения могут достигаться в точках экстремума и на границе области, поэтому для их отыскания поступают следующим образом:

• определяют стационарные точки функции и вычисляют значения функции в тех стационарных точках, которые содержатся внутри заданного множества;

• вычисленные значения функции сравнивают между собой и со значениями функции на границе области. Среди них находят наибольшее и наименьшее.

Пример

Найти наибольшее и наименьшее значения функции в области, ограниченной координатными осями и прямой .