Решение
По формуле полного дифференциала
.
Частные производные равны:
, 
.
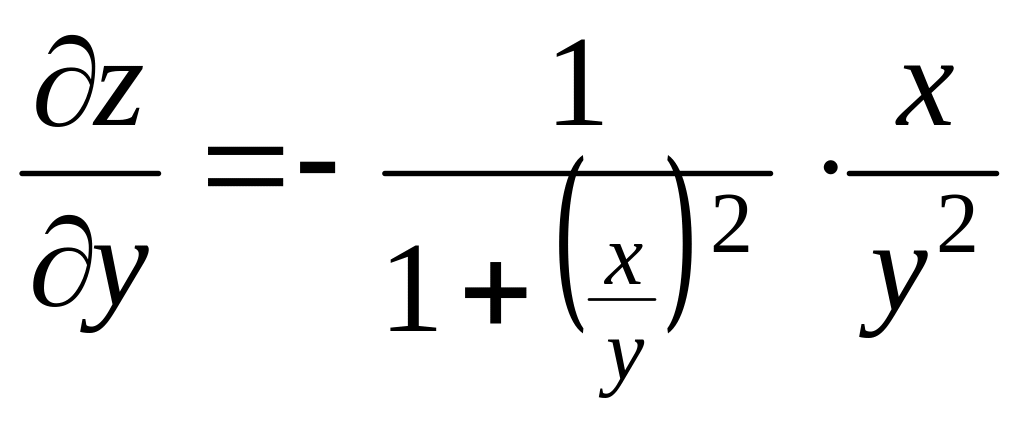Вычислим значения частных производных
в точке
:
,
.
Подставляя эти значения, а также значения
и
в формулу дифференциала, получим
.
Из определения дифференциала
функции нескольких переменных
следует важный вывод. В тех случаях,
когда модули приращений
достаточно малы, можно заменять приращение
функции в некоторой точке
ее дифференциалом, так как они отличаются
на бесконечно малую более высокого
порядка, чем
.
Погрешность, появляющаяся при такой
замене, не превосходит
.
Этим пользуются при вычислении
приближенных значений дифференцируемых
функций.
Пример
Вычислить приближенно
.
Решение
Рассмотрим функцию
.
Необходимо вычислить ее значение в
точке
.
Представим
,
где
,
.
Тогда
.
Теперь представим
и
.
Так как
,
то
,
а
.
Поскольку
и
достаточно малы, то заменим приращение
функции
ее дифференциалом
.
Для этого вычислим частные производные
и
в точке
.
Получим
и
.
Тогда дифференциал в точке
при
и
равен
.
Следовательно, приближенное значение
функции равно
.
При этом верхняя граница абсолютной
погрешности
определяется
из равенства:
.
В рассмотренной задаче
.
8. Геометрический смысл дифференциала функции двух переменных. Уравнение касательной плоскости и нормали к поверхности.
Теорема
Если функция
- дифференцируема в точке
,
то существует не параллельная оси
касательная плоскость к поверхности
в точке
,
уравнение которой имеет вид
,
где (рис. 4).
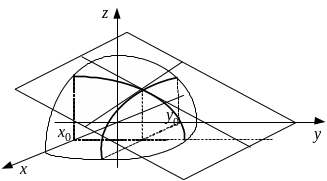
Рис. 4.
Следствие 1
Если поверхность задана уравнением
,
и функция
дифференцируема в точке
,
то уравнение нормали к этой поверхности
в точке
,
где
,
имеет вид:
.
Следствие 2
Полагая в уравнении касательной плоскости
,
и
,
можно установить, что
,
то есть дифференциал функции двух переменных равен приращению аппликаты касательной плоскости.
Пример
Напишите уравнения касательной плоскости
и нормали к поверхности, заданной
уравнением
в точке
.
Решение
Частные производные заданной функции
равны
,
.
Вычислим значения частных производных
в точке
:
,
.
Значение функции в точке
.
Тогда уравнение касательной плоскости
имеет вид:
,
или
.
Уравнение нормали:
.
9. Частные производные и дифференциалы высших порядков функции двух переменных
Пусть функция имеет частные производные в точке из ее области определения . Будем называть их частными производными первого порядка. Так как они являются функциями тех же переменных, что и данная функция, то у каждой из них могут существовать частные производные по любому из этих аргументов.
Полученные таким образом частные производные называются частными производными второго порядка.
Для функции двух переменных можно составить четыре частных производных второго порядка, которые обозначаются следующим образом:
;
;
;
.
Вообще для каждой из этих частных производных второго порядка можно дать и строгое определение.
Определение 1
Если существует и конечен
,
то он называется частной производной
второго порядка от
по
дважды в точке
и обозначается
или
.
Аналогично даются строгие определения для остальных частных производных второго порядка. Частные производные от частных производных второго порядка называются частными производными третьего порядка, и.т.д.