§ 5.4. Разбиения

Пусть М – множество мощности n, {M₁,M₂,...,M_k} – разбиение множества М на k подмножеств, |M_i| = m_i, m₁ + m₂ + ... + m_k = n. Кортеж (M_1,…,M_k) называется упорядоченным разбиением множества М.

Если k = 2, то упорядоченное разбиение множества М на два подмножества, имеющие соответственно m₁ и m₂ элементов, определяется сочетанием (без повторений) из n элементов по m₁ или из n по m₂ (m₂ = n - m₁). Следовательно, число разбиений R(m₁,m₂) равно биномиальному коэффициенту С_n^m1 = С_n^m2. Таким образом,

В общем случае число R(m₁,m₂,…,m_k) упорядоченных разбиений (M₁,M₂,...,M_k), для которых |M_i| = m_i, равно , а число R(n,k) упорядоченных разбиений на k подмножеств вычисляется по формуле

Числа R(m₁,m₂,…,m_k) называются полиномиальными коэффициентами, поскольку для всех а₁,а₂,…,а_k R справедливо соотношение

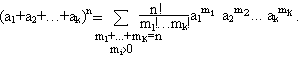
П р и м е р 5.4.1. В студенческой группе, состоящей из 25 человек, при выборе старосты за выдвинутую кандидатуру проголосовали 12 человек, против – 10, воздержались – 3. Сколькими способами могло быть проведено такое голосование?

Пусть М – множество студентов в группе, М₁ – множество студентов, проголосовавших за выдвинутую кандидатуру, М₂ – множество студентов, проголосовавших против, М₃ – множество студентов, воздержавшихся от голосования. Тогда |М| = 25, |М₁| = 12, |М₂| = 10, |М₃| = 3, (М₁,М₂,М₃) – упорядоченное разбиение множества М. Искомое число R(12,10,3) равно .

Число R(m₁,m₂,…,m_k) разбиений исходного множества М на k подмножеств М₁,М₂, . . . , М_k, |M_i| = m_i, неупорядоченных между собой, вычисляется по формуле

а число всех возможных разбиений множества М на k подмножеств неупорядоченных между собой, равно

П р и м е р 5.4.2. Сколькими способами из группы в 25 человек можно сформировать 5 коалиций по 5 человек?

Пусть Х – множество людей в группе, m_i – число коалиций по i человек, где i = 1,…,25. Тогда по условиям задачи |М| = 25, m₅ = 5, m_i =0, i {1,2,…,25} \ {5}, и, следовательно, искомое число будет равно

§ 5.5. Метод включений и исключений

Пусть множество А имеет N элементов и n одноместных отношений (свойств) Р₁,Р₂,…,Р_n. Каждый из N элементов может обладать или не обладать любым из этих свойств. Обозначим через N_{i1...i k} число элементов, обладающих свойствами Р_i1,...,P_{i k} и, может быть, некоторыми другими. Тогда число N(0) элементов, не обладающих ни одним из свойств Р₁,Р₂,…,Р_n, определяется по следующей формуле, называемой формулой включений и исключений:

N(0) = S₀ – S₁ + S₂ - ... + (-1)ⁿ S_n , (5.2)

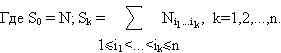
П р и м е р 5.5.1. Пусть колода состоит из n карт, пронумерованных числами 1,2,…,n. Сколькими способами можно расположить карты в колоде так, чтобы ни для одного i (1 ≤ i ≤ n) карта с номером i не занимала i-e место?

Имеется n свойств Р_i в виде «i-я карта занимает в колоде i-е место». Число всевозможных расположений карт в колоде равно n!. Число N_{i1...i k} расположений, при которых карта с номером i_j занимает место i_j (j=1,...,k), равно (n-k)!. Тогда S₀ = n!,

Используя формулу (5.2), получаем, что число N(0) расположений, при которых ни одно из свойств Р_i не выполнено, равно

Обобщая формулу (5.2), получаем формулу, позволяющую вычислить число N(r) элементов, обладающих ровно r свойствами (1 ≤ r ≤ n):

(5.3)

В § 3.4 мы определили функцию [x] для вещественных чисел х как наибольшее целое число, не превосходящее х. Для положительных целых чисел a и b значение функции равно количеству чисел из множества {1,2,…,b}, которые делятся на а, т.е. кратных а.

П р и м е р 5.5.2. сколько положительных чисел от 1 до 500 делятся ровно на одно из чисел 3,5 или 7?

Обозначим свойства делимости на 3,5 и 7 соответственно через Р₁, Р₂ и Р₃. Тогда для N = 500 имеем , , . Так как N₁₂ – число общих кратных для чисел 3 и 5, наименьшее общее кратное которых равно 15, то N₁₂ совпадает с количеством чисел, которые делятся на 15, т.е. . Аналогично , , . По формуле (5.3) находим искомое число чисел

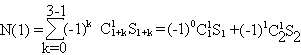
-2( N₁₂ + N₁₃ + N₂₃) + 3N₁₂₃ = 166 +100 +71 -2(33+23+14) +3 4 =209.