Изменение энтропии при кристаллизации переохлажденной жидкости

Здесь рассматривается неравновесный процесс: , который моделируется в квазиравновесный, путем разбивания на стадии.

1. Нагревание жидкости до точки плавления

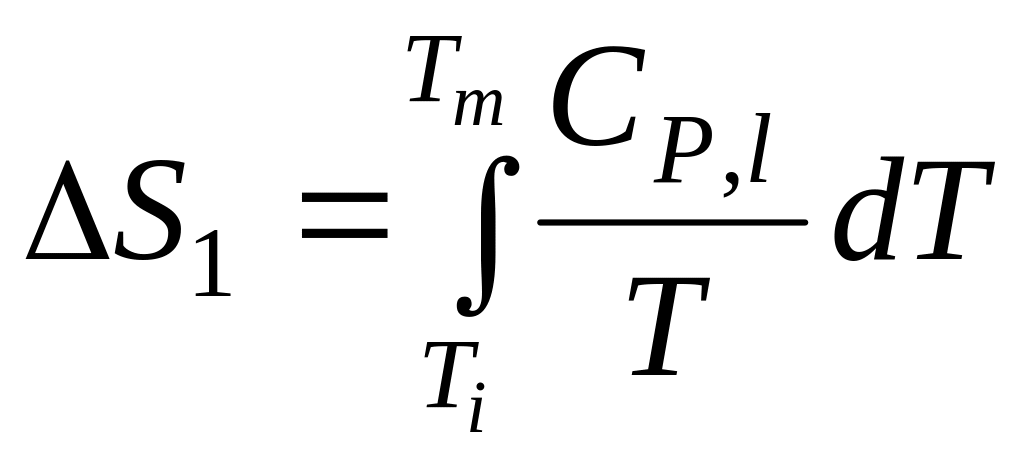
2. Кристаллизация жидкости при температуре плавления T_m

3. Охлаждение твердого вещества от T_m до T_i

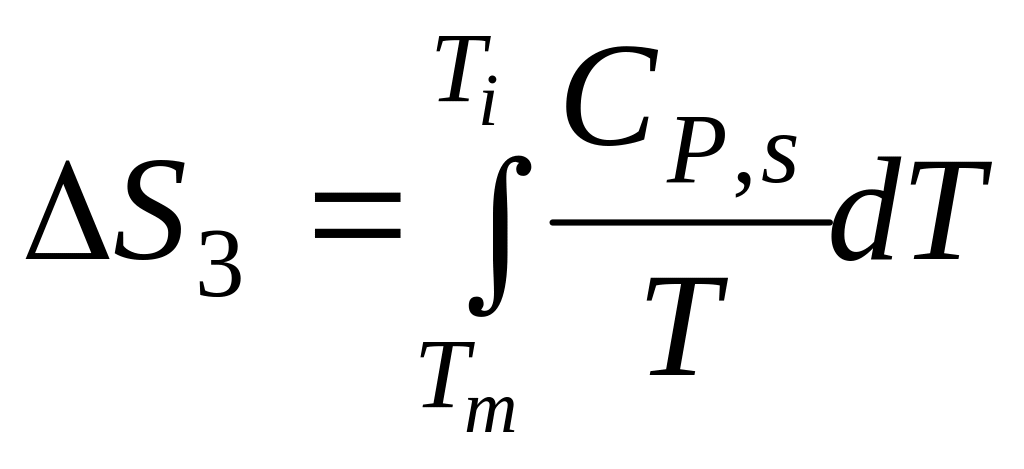
Итого:

Изменение энтропии химической реакции

В силу того, что энтропия – функция состояния, то к ней применим закон Гесса:

,

где ν – стехиометрический коэффициент; индекс i относится к исходным веществам, индекс k – к продуктам реакции. – энтропия образования вещества, приведенная к стандартным условиям при температуре Т.

Зависимость изменения энтропии химической реакции от температуры описывается уравнением: .

Изменение энтропии идеального газа

Выводится из уравнения, объединяющего I и II законы термодинамики:

Или

Откуда

Если считать, что теплоемкость не зависит от температуры, то после интегрирования:

Эти уравнения позволяют рассчитывать изменение энтропии 1 моль идеального газа при переменных T, V и P.

Для изотермического расширения ИГ

Для изохорного или изобарного нагревания

Для образования 1 моль смеси идеальных газов

Для смеси из двух газов:

Термодинамические потенциалы

Из уравнения I и II начал термодинамики выводится, что для изолированных систем критерием самопроизвольности протекания процесса является изменение энтропии: dS > 0. Для состояния равновесия в изолированной системе нужно выполнение условия dS = 0.

На практике используются системы закрытые либо открытые. Следовательно, необходим вывод критерия, который бы отвечал двум требованиям:

1) позволял прогнозировать направление протекания процесса в любых условиях его проведения;

2) его можно было вычислить исходя из термодинамических характеристик системы.

В качестве подобного критерия была разработана система термодинамических потенциалов (Гиббс, Гельмгольц, Дюгем).

Термодинамический потенциал – максимальная работа, которую может совершить система при обратимом протекании процесса в данных условиях.

Тогда если система совершает по ходу процесса работу, меньшую, чем максимальная, то такой процесс идет самопроизвольно: или состояние равновесия

Объединенное уравнение первого и второго законов термодинамики можно записать в виде

для простой системы

для сложной системы

В простой системе осуществляются обратимые процессы:

В сложной системе осуществляются обратимые процессы:

Для систем, единственным видом работы которых является работа расширения (простые системы) четыре вида условий взаимодействия системы с окружающей средой:

Ситуация V,S = const

Объединенное уравнение первого и второго законов термодинамики для простой системы:

Очевидно, что для протекания процесса необходимо условие , а для равновесия .

В данном случае внутренняя энергия будет термодинамическим потенциалом (изохорно-изоэнтропийным) и критерием возможности самопроизвольности протекания процесса.

Ситуация Р,S = const

Согласно преобразованию Лежандра

Для простых систем

Тогда уравнение можно преобразовать к виду

Очевидно, что для протекания процесса необходимо условие , а для равновесия .

В данном случае энтальпия будет термодинамическим потенциалом (изобарно-изоэнтропийным) и критерием возможности самопроизвольности протекания процесса.

Ситуация V,T = const

Термодинамическая функция F=U – TS называется функцией Гелъмголъца, или изохорно-изотермическим потенциалом. Поскольку эта функция образована из функций состояния U и S, она также является функцией состояния.

Очевидно, что для протекания процесса необходимо условие , а для равновесия .

Таким образом с приближением системы к состоянию равновесия изохорно-изотермический потенциал убывает, достигая минимума в состоянии равновесия.

Ситуация Р,T = const

Р,T = const, следовательно W = 0.

Термодинамическая функция G = H – TS называется функцией Гиббса, или изобарно-изотермическим потенциалом. Поскольку эта функция образована из функций состояния U и S, она также является функцией состояния.

Очевидно, что для протекания процесса необходимо условие , а для равновесия .

Для сложных систем в перечисленных ситуациях критерии самопроизвольности протекания процесса те же самые. Преобразования уравнения приведут к следующим результатам.

V,S = const

В состоянии равновесия работа равна убыли внутренней энергии

V,T = const

В состоянии равновесия работа равна убыли энтальпии

V,T = const

В состоянии равновесия работа равна убыли энергии Гельмгольца

Р,T = const

В состоянии равновесия работа равна убыли энергии Гиббса

Функции U, H, F, G называются характеристическими.

Работа, которая может быть совершена сложной системой при данных условиях взаимодействия с окружающей средой (за вычетом работы расширения), равна убыли соответствующих характеристических функций. Поскольку в состоянии равновесия работа, совершенная системой, максимальна при определенных внешних условиях, по этой причине характеристические функции U, И, F, G называют термодинамическими потенциалами.