2.4. Двоїста задача лінійного програмування

Для кожної моделі існує поняття двоїстої задачі (Dual task), тобто запис задачі іншими змінними для розв’язання потім іншим методом, який потрібен для перевірки правильності симплекс-методу та для інших методів ЛП. Є також ряд задач лінійного програмування, які можуть бути розв’язані тільки двоїстим симплекс-методом, наприклад, деякі задачі мінімізації. Двоїста задача використовується, наприклад, для зменшення розмірності задачі, а також для розрахунку псевдоплану ДСМ (двоїстого симплекс-методу). Якщо пряма задача має розмірність m*n, то її можна записати та розв’язати як задачу розмірністю n*m. Математична модель двоїстої задачі має вигляд:

.

Теорема 1: значення ЦФ прямої та двоїстої задач співпадають, а знаки – ні, тобто якщо в прямій задачі Z  max, то в двоїстій: Z  min. Якщо в прямій задачі функція необмежена зверху, то в двоїстій – знизу.

Теорема 2: пряма та двоїста задачі взаємопов’язані одна з одною такими формулами:

Двоїста задача (ДЗ):			Пряма задача (ПЗ):
	x1			y1
…	…		…	…
	xn			ym

Правила переведення до двоїстої задачі (ДЗ):

1. Кожному обмеженню типу «=» ПЗ відповідає змінна ДЗ.

2. Кожній змінній ПЗ відповідає обмеження виду «<» чи «>» ДЗ.

3. Коефіцієнти цільової функції ДЗ дорівнюють правій частині ПЗ.

4. Якщо для ПЗ умова невід’ємності обов’язкова, то для ДЗ – відсутня.

5. Цільова функція змінює знак з max на min або навпаки.

6. Обмеження ДЗ мають знак «», якщо в ПЗ z  max.

7. Існує взаємозв’язок між змінними двоїстої та прямої задач:

…		…

Отримавши результат – вектор y, можна на базі описаної системи знайти вектор X. Для розв’язання прямої задачі потрібно:

* перейти від прямої моделі до двоїстої: f(x)f(y);

* розв’язати ДЗ (знайти вектор Y);

* на підставі зазначеної системи знайти вектор X.

Р

	y1
	y2
	(1)
	(2)
	(3)
	(4)

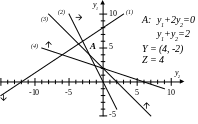озглянемо приклад:

На підставі теореми 2 запишемо наступні рівняння та розв’яжемо задачу методом підбору, тобто знайдемо вектор Y, і підставимо його у вихідну систему рівнянь:

Y=(4; -2)

X = ( 0 , 2, 2, 0)

Z = 4.

Доцільність використання ДЗ полягає в зменшенні розмірності та кількості змінних задачі. Двоїста задача використовується також в інших задачах (наприклад, двоїстий симплекс-метод).