8.2. Загальний алгоритм складання розкладу занять

з використанням методів дослідження операцій ......................97

8.3. Класифікація методів технічного пошуку рішень ..................99

8.4. Моделювання гнучкості для забезпечення властивості бути керованим .............................................................................101

Контрольні запитання ....................................................................105

СПИСОК ЛІТЕРАТУРИ .....................................................................106

ВСТУП

У посібнику, в якому розглянуто математичні методи дослідження операцій в інформаційно-управляючих системах та технологіях, в одному методологічному плані викладені різні за характером матеріали: основні визначення дослідження операцій (ДО), аспекти лінійного, нелінійного та динамічного програмування, моделі оптимізації на мережах, а також розв’язання деяких практичних задач у будівництві та інших галузях з використанням комп’ютерних технологій.

Незважаючи на велику кількість навчальних посібників та наукової літератури з моделей оптимізації, роботи, в яких ці питання були б висвітлені компактно, повністю та з практичним ухилом від складання моделей до реалізації програмного забезпечення, поки що відсутні. Крім того, література часто викладена у великому обсязі, громіздка для вивчення та ускладнена. Це все призводить до гальмування використання апарату оптимального прийняття рішень у навчанні та практиці і до недостатньої формалізації програмних розробок проектування і управління. Також при викладанні матеріалу важливо мати досвід програмної реалізації методів оптимального управління, дослідження їх на великих розмірностях та впровадження в практику. Цей досвід автор має та викладає в даному посібнику. Більшість алгоритмів та методів викладені інакше, ніж в іншій літературі, з прикладами та фрагментами комп’ютерних програм.

Звісно, при вивченні матеріалу «з нуля» одного лише посібника не завжди достатньо. Ще треба мати пакет прикладних програм з кожного методу та набір початкових даних у файлах. Програма «автоматизований метод» має в режимі навчання роздруковувати та пояснювати ітерації обчислювального процесу. Лектор же забезпечує такими програмними продуктами студентів. Лише тоді посібник даватиме теоретичні основи з можливістю їх експериментального дослідження.

Навчальний посібник складається з шести розділів, кожний з яких вміщує такі питання, як загальні визначення з методу чи моделі, короткий опис алгоритму, приклади розв’язання типових задач з використанням методів, рекомендації щодо їх використання та контрольні запитання до розділу. Запитання побудовані таким чином, що так просто відповідь в тексті знайти не можна. Щоб відповісти на них, потрібно знати матеріал з точки зору його практичного використання.

1. Загальні визначення, класифікація моделей і методів

1.1. Загальні визначення дослідження операцій

Метою дослідження операцій як науки є прийняття оптимальних управлінських рішень на основі досвіду моделювання задач у різних прикладних областях та з використанням моделей, методів і прикладного програмного забезпечення.

Дослідження операцій – це наука про моделі, методи оптимізації та системи оптимального прийняття рішень. Володіючи основами науки «Дослідження операцій» (ДО), користувач створює математичну модель задачі в предметній області, приводить її до типової моделі та задачі, аналізує існуючі методи розв’язання проблеми, обирає один або декілька методів та існуючі для них програмні засоби і зрештою розв’язує задачу на комп’ютері. Отримавши «вектор-результат», користувач його аналізує, повертається до початкової моделі задачі в предметній області, досліджує модель для різних початкових змінних та пропонує варіант оптимального розв’язання цієї задачі чи проблеми.

Дослідження операцій має велике значення як наука про прийняття оптимальних рішень у різних галузях. У результаті вивчення дисципліни користувач, крім знань та вмінь розв’язувати задачі, має зібрати на власному компакт-диску перелік типових задач та моделей, їхніх розв’язків з друком ітерацій рішень, а також пакет програмних засобів з основних методів дослідження операцій (ППДО). Цей пакет застосовуватиметься в різних дисциплінах навчання чи безпосередньо на робочому місці.

Математична модель – це умовний (штучний) математично представлений об’єкт з певним рівнем адекватності щодо його самого. Створення математичних моделей користувачем залежить, у першу чергу, від досвіду та кількості розроблених моделей. Тому необхідно з самого початку систематизувати типові моделі та задачі, а також накопичувати банк моделей та розв’язків різних задач у різних предметних областях.

Математичне моделювання використовується в різних областях науки, але моделювання з використанням дослідження операцій суттєво відрізняється за наступними ознаками:

_{* наявність прямуючої до оптимуму (екстремуму) цільової функції;}

_{* наявність обмежень з різними знаками («=», «>=», «<=»);}

_{* додаткові умови («невід’ємність», «цілочисельність» тощо);}

_{* взаємозв’язок змінних цільової функції, обмежень і додаткових умов;}

_{* належність до конкретної математичної області (лінійне, нелінійне, динамічне програмування, оптимізація на мережах тощо);}

_{* модель ДО розв’язується як мінімум двома методами;}

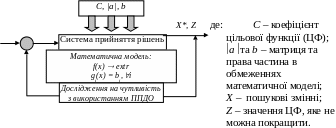_{* математичну модель з використанням ДО можна доповнити схемою:}

З метою розуміння можливостей ДО розглянемо деякі види задач, що можуть розв’язуються графоаналітичним методом.