У комп’ютерній програмі стратегія реалізується таким чином.

1. Кожен рівень дерева x₁, x₂, …x_n – це файл прямого доступу «Х1.bak», «Х2.bak», …«Хn.bak».

2. Записи файла прямого доступу – це вузли рівня. Кожний запис містить оцінку та рекорд розрахунків, а також адресне посилання на «батьківський» запис у попередньому файлі.

Примітка. Приклад дискретного динамічного програмування вже розглянутий в п. 4.2.

Розгалуження з обмеженням в довжину (ширину) має стратегію подібну «лавиноподібному», але побудова дерева варіантів обмежується за кількістю рівнів та вузлів (параметричне динамічне програмування). Суть метода така.

1. Визначення параметрів D₁ (кількість рівнів) та D₂ (кількість вузлів).

Примітка. D₁ та D₂ визначаються експериментально в процесі налаштування програми та можуть задаватися по різному, наприклад: D₁ = 3; D₂ = max (4,7,∞).

2. Генерування D₁ рівнів і вибір D₂ найкращих вузлів. Визначення z^* – ймовірного кращого розв’язку з них.

3. Повернення на вищий рівень відносно z^* та рекурсивне виконання пунктів 2 і 3 відносно поточного рівня до одержання задовільного (або точного) розв’язку.

З а допомогою стратегії розв’язуються задачі ЦЛП з використанням симплекс-методу. Схематично дерево розгалужень можна уявити як «три кроки вперед та два кроки назад» (наприклад, D₁ = 2 та D₂ = 4):

D₁ = 2,

D₂ = 4.

x₁

z^*

x₂

z^*

x₃

z

x₄

Однобічне розгалуження має стратегію вибору на кожному рівні дерева серед необмеженого числа вузлів одного найкращого для його подальшого рекурсивного розгалуження, отже дерево рішень будується однобічно. Ця стратегія не дає оптимального результату z, бо він часто втрачається у відсічених площинах:

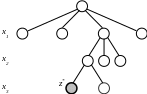
Н айкращим прикладом використання даної стратегії є розв’язок задачі про мінімальний остов (кістяк вузлів). Остов – це дерево, яке охоплює всі вузли мережі та при цьому не виникає циклів. Мінімальний остов – це остов, сума довжин дуг якого мінімальна. Приклад:

Обираємо найкоротшу дугу (1-2), потім найкоротшу, пов’язану з нею – (2-5), потім найкоротшу, пов’язану з (1-2-5) – (5-4), таким чином, охоплюючи всі вузли мережі. Подібний алгоритм для задачі про мінімальний остов дає мінімальний результат, в якому реалізована сама ідея: на кожному кроці брати наступний, найближчий до остова, вузол.

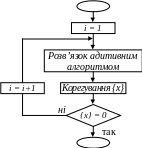
Back-track («зворотний промінь») технологія використовується для розв’язання задач «булева» оптимізації (адитивний алгоритм).

Примітка. Адитивний алгоритм вже розглянутий в п.4.2.

Розглянемо використання back-track технології на прикладі задачі про розсилання деякого числа файлів різного розміру по e-mail за деяке число сеансів, причому кожен сеанс має своє обмеження на обсяг даних. Суть задачі полягає в пошуку найінтенсивнішого режиму розсилання.

Розмір файлів, МБ	1.2	0.5	0.7	1	0.4	0.2
Розмір сеансів, МБ	1.5	1	1	1.5

Цільова функція:

1-а ітерація:

Пошук полягає в побудові дерева з кількістю рівнів еквівалентною кількості х_i в обмеженнях і кількістю «дочірніх» вузлів для кожного вузла х_i рівною кількості можливих значень для кожного х_i+1 (у цьому випадку варіант можливих значень – 0 або 1). На кожному етапі варіанти, що не відповідають обмеженню, відкидаються, неперспективні варіанти (згідно прогнозу) відкладаються на потім, а можливі варіанти отримують оцінку з фіксацією рекорду. Ітерація продовжується доти, доки не відбудеться повернення до початкового вузла. Всього в задачі 4 ітерації (сеанси).

Відповідь: x₂, x₄, x₃, x₆, x₅, x₁.