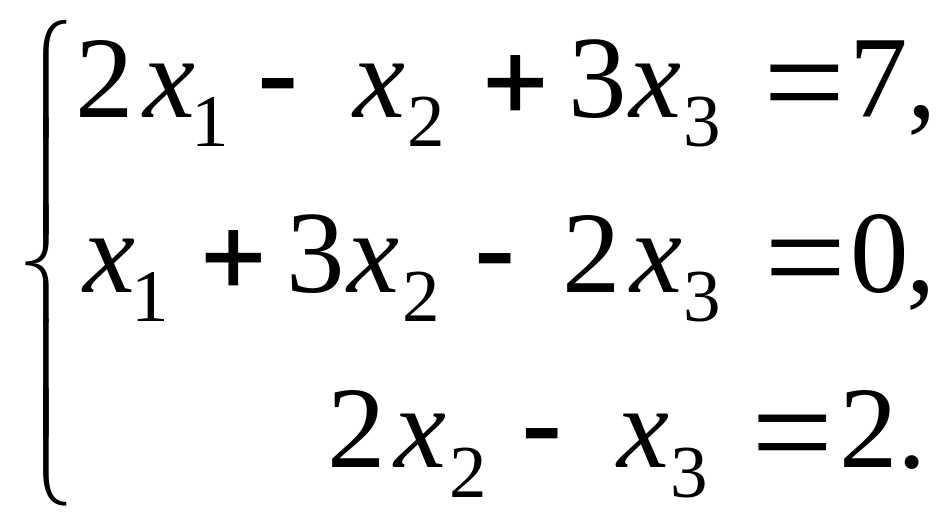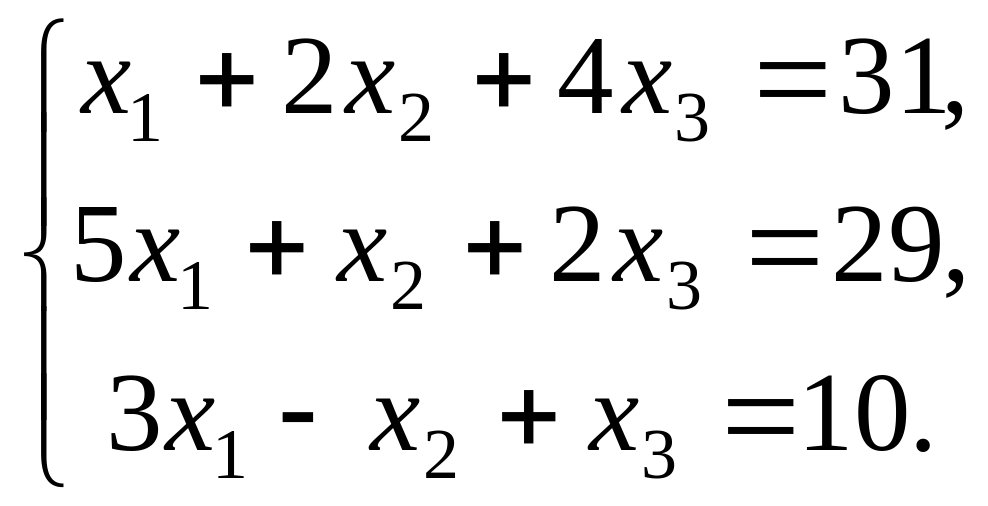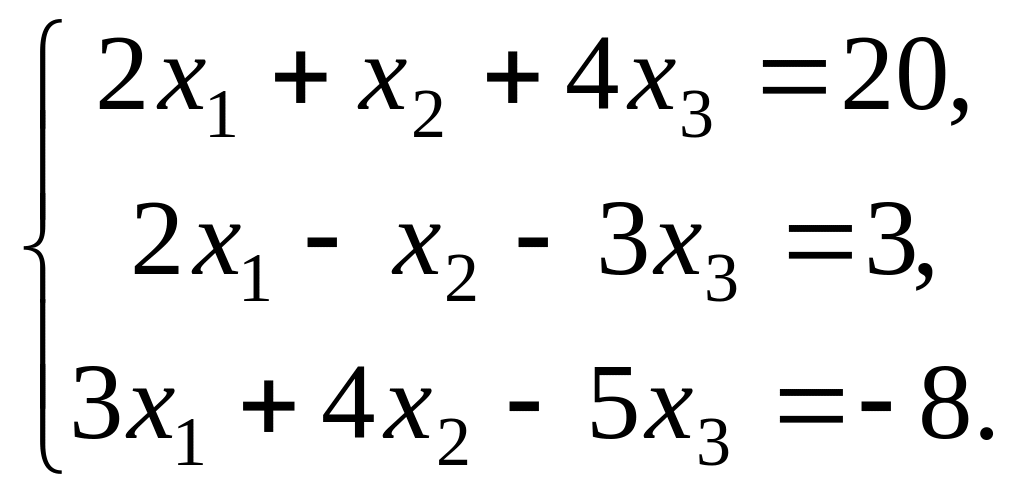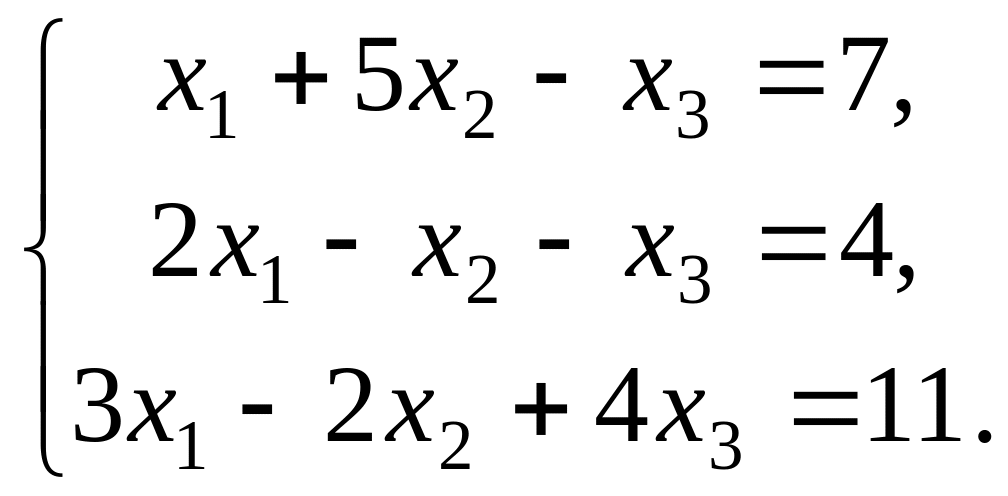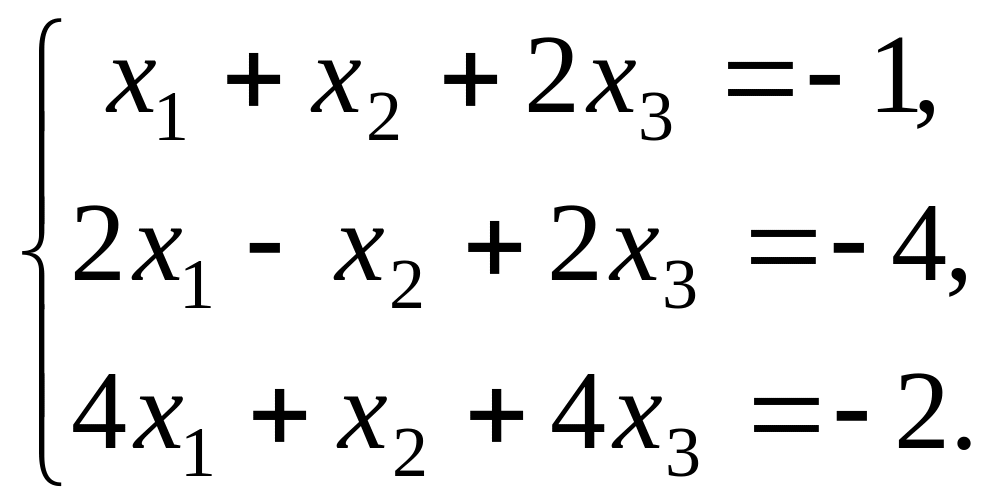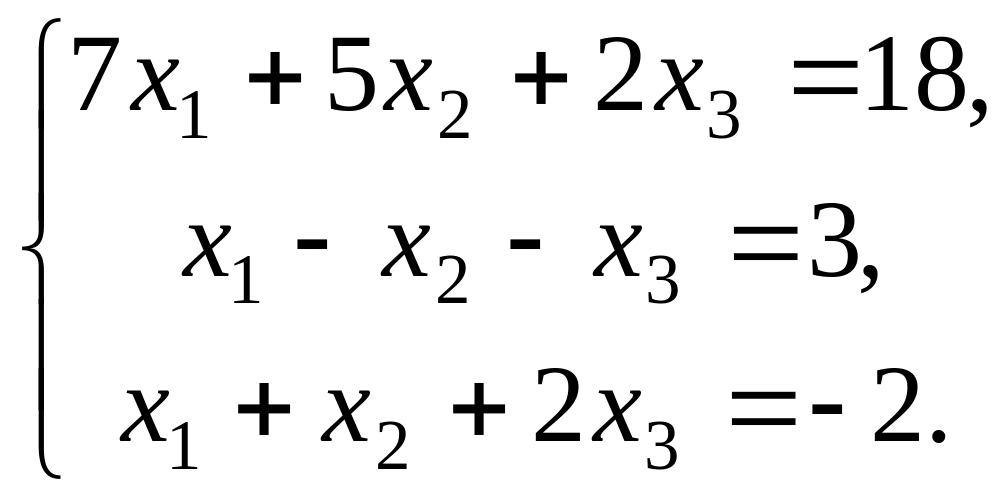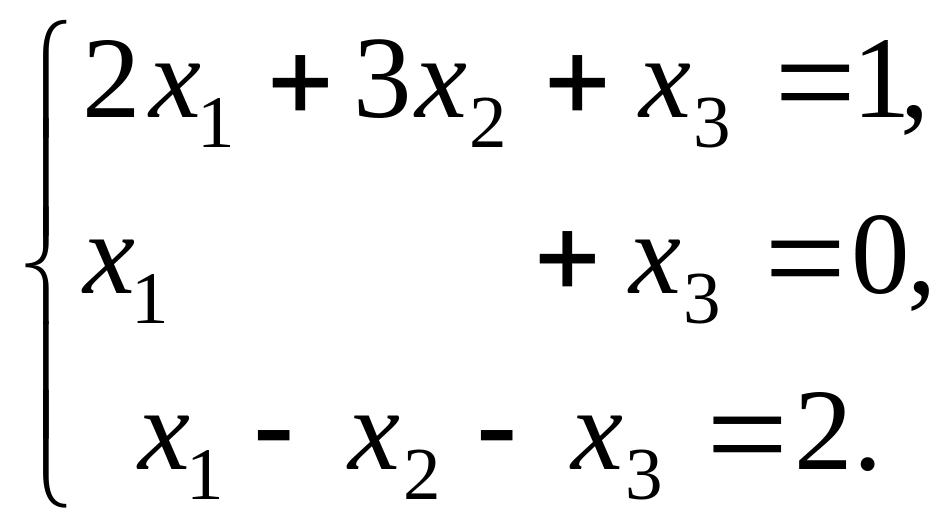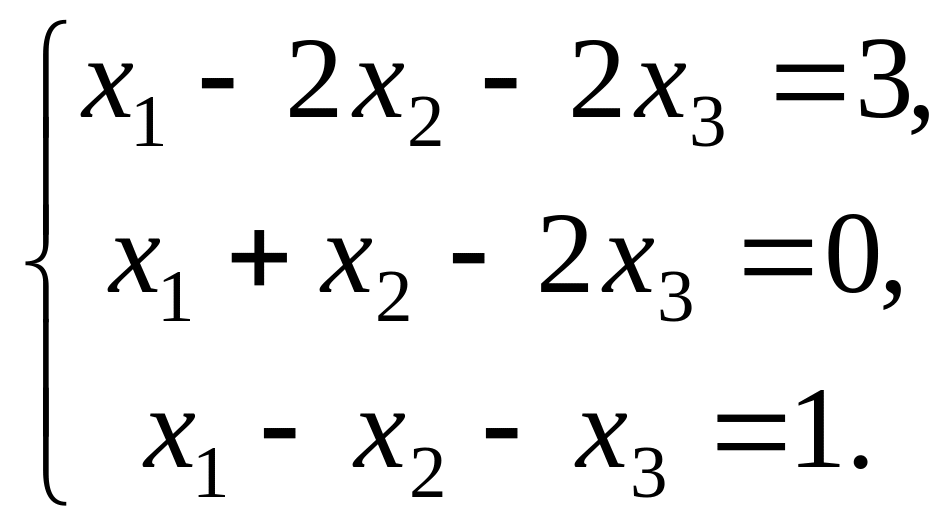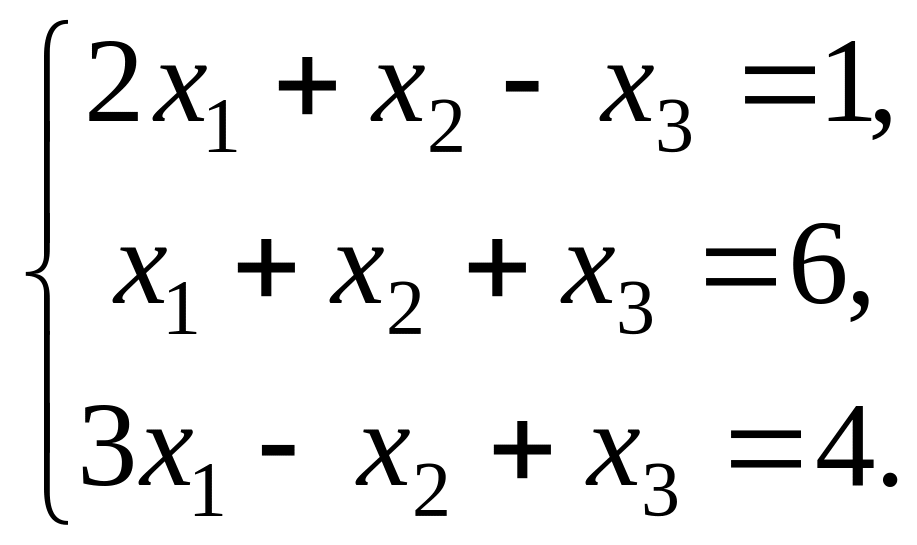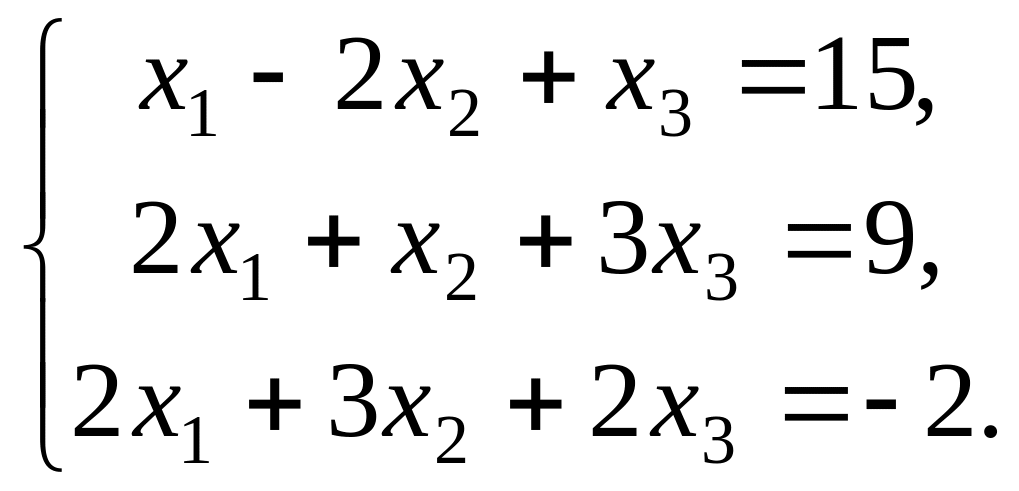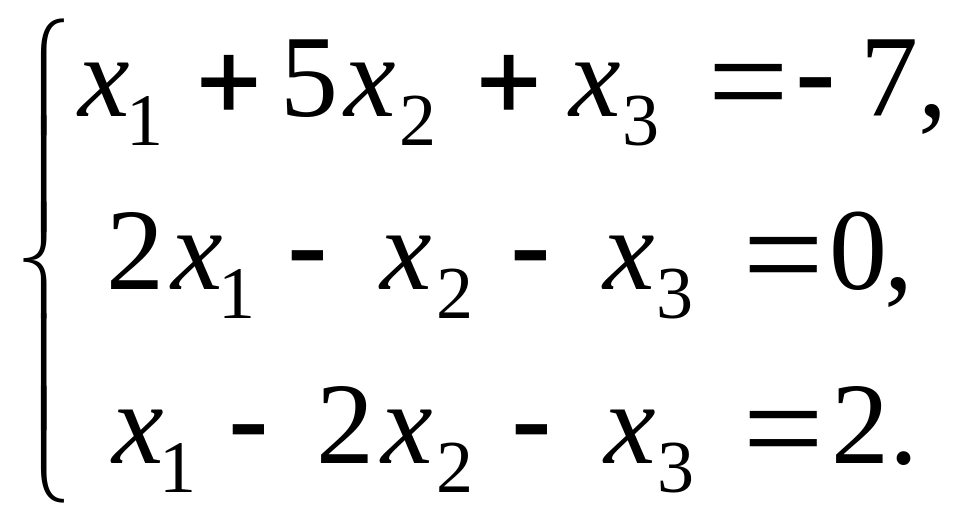Варианты для выполнения Задания 2.1
Синтезировать структурную схему моделей статических систем и получить соответствующее решение.
При построении модели можно использовать следующие блоки: Constant, Integrator, Gain, Trigonometric Function, Math Function, Sum, Product, Mux, Display, Scope, Algebraic Constraint.
№ |
Система 1 |
Система 2 |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
Задание 2.2
Найти решение системы линейных алгебраических уравнений:
Модель решения системы уравнений представлена на рис. 2.6.
Решение системы уравнений, отображенное
на цифровых регистраторах (Display1 –
Display3), равно
Переходный процесс получения установившегося решения изображен на экране виртуального осциллографа (рис. 2.7).
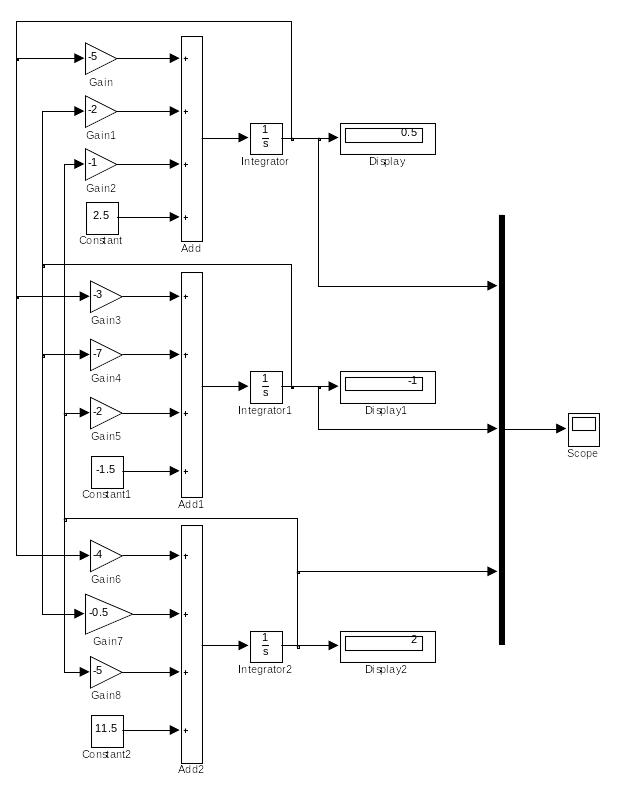Рис.
2.6 Модель системы линейных алгебраических
уравнений 3 порядка
Рис.
2.7 Переходный процесс установления
решения системы уравнений
Варианты для выполнения Задания 2.2
Синтезировать структурную схему модели статической системы и получить соответствующее решение.
При построении модели можно использовать следующие блоки: Constant, Integrator, Gain, Mux, Sum, Product, Scope, Display, Algebraic Constraint.
№ |
Система |
№ |
Система |
1 |
|
14 |
|
2 |
|
15 |
|
3 |
|
16 |
|
4 |
|
17 |
|
5 |
|
18 |
|
6 |
|
19 |
|
7 |
|
20 |
|
8 |
|
21 |
|
9 |
|
22 |
|
10 |
|
23 |
|
11 |
|
24 |
|
12 |
|
25 |
|
13 |
|
|
|
тематическое задание №3 ПОСТРОЕНИЕ непрерывно-детерминированных МОДЕЛЕЙ динамических объектов и процессов
Цель работы
Определение динамических объектов и процессов.
Моделирование динамических объектов и процессов.
Теоретическая подготовка к выполнению работы
Перед выполнением лабораторной работы необходимо ознакомиться с темами:
Понятия о динамических объектах и процессах и способах их моделирования.
Библиотека блоков SIMULINK [1, п.9].
Ответить на вопросы: