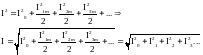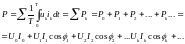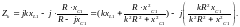4.2.4 Датчик тока с логическим выходом

Датчики тока с логическим выхо­дом (рис. 14) позволяют обнару­жить превышение тока в контролиру­емом проводнике выше определенного значения и сформировать логический сигнал тревоги. Основой этих приборов являет­ся интегрированный датчик Холла с логическим выходом.

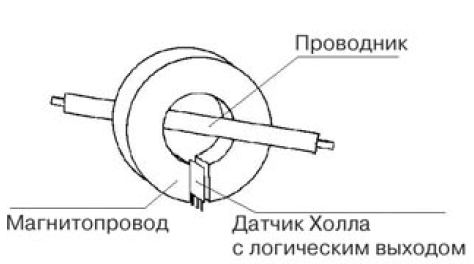
Рисунок 14 - Структура датчика тока с логическим выходом

Значение порога срабатывания опре­деляется моделью датчика и может иметь следующие значения: 0,5; 3,5; 5,0; 7,0; 10,0 и 54,0 А. Порог сра­батывания может быть установлен меньше номинального значения путем увеличения числа витков проводника вокруг кольца датчика.

4.2.5 Материалы для изготовления датчиков Холла

Полупроводниковый материал, предназначенный для изготовления ДХ, должен обладать не только высокими, но и по возможности мало зависящими от температуры значениями постоянной Холла и подвижности носителей тока. Выбор полупроводникового материала для ДХ диктуется областью его применения.

Как правило, используются полупроводники с электронной проводимостью, поскольку они имеют значительно большую подвижность носителей заряда, чем полупроводники с дырочной проводимостью. Необходимо подчеркнуть, что свойства каждого из указанных полупроводниковых материалов могут существенно изменяться в зависимости от рода и количества примесей, вводимых в них.

Кристаллические датчики обычно изготавливают из германия, кремния, полупроводниковых соединений элементов третей и пятой групп периодической системы Менделеева – антимонида индия, арсенида индия, арсенида галлия, а также твердого раствора – тройного соединения In(As0,8P0,2) [6].

4.3 Мощность искажения

Если представить периодический несинусоидальный ток рядом Фурье, то:

i= I₀ + I₁sin( +₁) + I₂sin(2 +₂) + + I_ksin(k+_k)+, а

.

Но 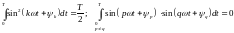, поэтому

Следовательно, действующее значение несинусоидального периодического тока равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник.

Проведя аналогичные выкладки, можно получить выражения для действующего значения падения напряжения в виде:

Средняя мощность P в цепи при несинусоидальных токах и напряжениях может быть выражена в виде:

.

Подставляя в это выражение напряжение и ток, представленные рядами Фурье, получим:

Но при p q все слагаемые второй суммы тождественно равны нулю, поэтому средняя мощность равна:

Из последнего выражения следует, что средняя или активная мощность в цепи с несинусоидальными токами и напряжениями равна сумме средних или активных мощностей отдельных гармоник.

По аналогии с цепями синусоидального тока можно ввести понятие полной или кажущейся мощности как произведение действующих значений тока и напряжения S = UI, тогда отношению P/UI можно придать смысл коэффициента мощности cosφ_э. Выражение cosφ_э = P/UI формально справедливо для некоторой электрической цепи синусоидального тока, в которой протекает ток с действующим значением I и существует падение напряжения U. При этом в цепи выделяется активная мощность P. Следовательно, несинусоидальные токи и напряжения, не содержащие постоянных составляющих, можно заменить эквивалентными им по действующему значению синусоидальными со сдвигом фаз между ними _э, соответствующим, коэффициенту мощности несинусоидальных величин. Кривые токов и напряжений в общем случае имеют различные спектры, поэтому для них не существует понятия угла сдвига фаз и _э имеет смысл только для эквивалентных синусоид.

В отличие от выражения для активной мощности в цепи несинусоидального тока, полученного из понятия средней за период величины, реактивную мощность определить таким образом невозможно. В цепях синусоидального тока она определяется через амплитуду или среднее значение за четверть периода одной из переменных составляющих мгновенной мощности. Поэтому для цепи несинусоидального тока ее можно определить только формально по аналогии с активной мощностью в виде Q = U₁I₁sin₁ + U₂I₂sin₂ + + U_kI_ksin_k +

В цепях несинусоидального тока не существует связи между активной, реактивной и полной мощностью в виде треугольника мощностей, то есть:

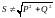
Расчет цепи при несинусоидальных токах проводится аналогично расчету при синусоидальных, но он должен выполняться отдельно для каждой гармоники в следующем порядке:

• представить действующую в цепи ЭДС или ток рядом Фурье;

• методом расчета цепей синусоидального тока произвести расчет отдельно для каждой гармоники спектра;

• по полученному спектру искомых величин найти требуемые значения.

Пусть требуется найти активную мощность в цепи рис. 15, где приложенное напряжение равно u(t)=10+20sin(1000t30 )+5sin(3000t+45) В, а параметры элементов R = 20 Ом, C = 50 мкФ и L = 5 мГн.

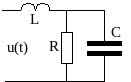
Рисунок 15 – Схема соединения элементов R, L, C

Спектр приложенного напряжения содержит постоянную составляющую или нулевую гармонику, а также первую и третью гармоники. Реактивные сопротивления цепи зависят от частоты. Для k-й гармоники их можно представить через сопротивления на частоте основной гармоники в виде:

где x_L1 = ₁L= 5 Ом и x_C1 = 1/(₁C) = 20 Ом - индуктивное и емкостное сопротивления на частоте основной гармоники. При расчете реактивных сопротивлений можно формально считать постоянную составляющую нулевой гармоникой. При этом x_L0 = 0, а x_C0 =  , что соответствует отсутствию этих элементов и вполне согласуется с теорией цепей постоянного тока, где в статических режимах реактивных элементов нет.

Общее комплексное сопротивление цепи на частоте k-й гармоники будет

Подставляя в это выражение значения k = 0, 1, 3, получим значения общих комплексных сопротивлений на всех гармониках в виде Z₀ = 20 Ом ; Z₁ = 10j5 Ом ; Z₃ = 2+j9 Ом . Из этих выражений видно, что комплексные сопротивления на разных частотах могут иметь реактивную составляющую разного знака.

Отсюда комплексные значения токов I₀ = U₀/Z₀ = 10/20 = 0.5 А; I₁ = U₁/Z₁ = 20e^j30/(10j5) = 1,78e^j3.4А; I₃ = U₃/Z₃ = 5e ^j45/(2+j9) = 0,54e^j32.4А.

Полученные комплексные значения составляющих спектра токов можно представить рядом Фурье в виде:

i = 0,5+1,78sin(1000t3.4 )+0,54sin(1000t32,4 ), А.

Теперь можно определить активную мощность в цепи как:

Для оценки формы кривых несинусоидальных токов и напряжений используют коэффициенты формы k_f, амплитуды k_A , искажений k_d, среднего значения k_ср, гармоник k_THD.

Коэффициентом формы - отношение действующего значения к среднему значению, взятому за период положительной полуволны, т.е.:

.

Для синусоидальных величин k_f  1.11.

Коэффициентом амплитуды - отношение амплитудного значения к действующему k_A = U_m/U. Для синусоиды это значение равно 1,414.

Коэффициент искажений - отношение действующего значения основной гармоники к действующему значению всего спектра, т.е. k_d = I₁/I. Для синусоиды k_d = 1:

Коэффициент среднего значения – отношение среднего значения несинусоидального тока к амплитудному. Для синусоиды k_ср = 0,673.

Среднее значение несинусоидального тока за полупериод зависит от начальных фаз составляющих гармоник, не зависит от наличия и величины четных гармоник и равно сумме средних значений токов всех нечетных гармоник с учетом их фаз в виде:

Среднее значение несинусоидального тока за период равно постоянной составляющей.

Коэффициент гармоник или несинусоидальности - отношение действующего значения высших гармоник к действующему значения основной гармоники, k_THD для синусоиды равно нулю.

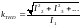
Поскольку идеальных синусоидальных величин практически не бывает, то в технике существует понятие практически синусоидальных кривых. Форма кривой считается практически синусоидальной, если все ее ординаты отличаются от ординат первой гармоники не более, чем на 5%. При этом количество контрольных точек должно быть не менее 12.

Приведенные выше аналитические зависимости позволяют определить мощность искажений при стендовых испытаниях вентиляторной установки [7].