2.14. Акустическое поле преобразователя.

Излучение преобразователя в среду описывается существенно разными закономерностями на близком и далеком расстояниях от преобразователя. В непосредственной близости от него ультразвук распространяется в виде параллельного пучка лучей, но чуть дальше картина несколько изменяется. Энергия по-прежнему остается в пределах нерасходящего пучка, но появляются максимумы и минимумы амплитуды (интенсивности). Вся эта область называется ближней зоной (Френеля) или ближнем полем.

В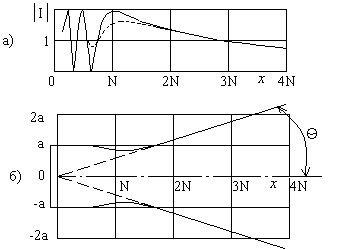 дальней зоне (дальнем поле) – зоне Фраунгофера, формируется расходящийся пучок лучей. Максимум амплитуды соответствует оси преобразователя (центральный луч). С увеличением угла между направлением какого-либо луча и осью амплитуда уменьшается. За пределами некоторого угла (угла раскрытия ') излучение почти не чувствуется. Угол раскрытия определяет направленность излучения.

Н

Рис. 2.24. Поле излучения на оси круглого преобразователя (а) и схематическое изображение поля (б).

а рис. 2.24, б показано схематическое изображение излучения в ближней и дальней зонах, а на рис. 2.24, а – изменение амплитуды излучения на оси. В ближней зоне амплитуда очень резко изменяется, а в дальней зоне – плавно уменьшается с увеличением расстояния от преобразователя. Также будет изменяться амплитуда сигнала, отраженного от маленького дефекта. Чем крупнее дефект, тем больше сглаживаются изменения амплитуды.

Протяженность ближней зоны N возрастает как размер (диаметр, сторона прямоугольника) пьезопластины преобразователя во второй степени и убывает с ростом длины волны ультразвука, т.е. с ростом частоты она растет, а с ростом скорости звука уменьшается (длины волны равна скорости звука деленной на частоту). Направленность излучения улучшается (угол расхождения уменьшается) с увеличением отношения размера преобразователя к длине волны. Обратим внимание, что для уменьшения расхождения лучей нужно увеличить размер преобразователя.

Область пространства, где действует излучение преобразователя, называется полем излучения. Распределение амплитуды в разных точках в пространстве описывает функция поля I(В). Поместим в какую-либо точку В источник, излучающий равномерно во все стороны. Сигнал, который примет преобразователь, в зависимости от положения точки В будет определять поле приема I'(В). Функция поля излучения – приема описывает изменение сигнала на приемнике, если в точку В поместить маленькую отражающую сферу. В области вблизи оси преобразователя (ее называют параксиальной, и именно она используется для контроля) I=I', поэтому поле излучения – приема определяется функцией I².

Возникновение максимумом и минимумов акустического поля в ближней зоне объясняется следующим. Преобразователь можно представить состоящим из большого количества маленьких излучателей. Расстояние от разных излучателей до некоторой точки В в ближней зоне могут сильно отличаться. Соответственно будут отличаться фазы приходящих сигналов. Например, если одинаково число излучателей, сигналы от которых приходят в противоположных фазах (т.е. от одних излучателей поступают волны, требующие растяжение объема около точки В, а от другой – его сжатия), то возникает минимум.

Наиболее удаленный от преобразователя максимум определяет границу ближней зоны. Он расположен на оси преобразователя в точке х = N (рис. 2.24,а). В этом случае сигналы от всех точек преобразователя приходят в точку N не в противоположных фазах, т.е. волны будут приходить с различным опозданием, но не будет волн, требующих сжатия объема, когда волна от центральной точки преобразователя требует его растяжения или наоборот. Для этого разница путей от краевой и центральной точек должна быть не больше /2, т.к. через /2 фаза растяжения сменяет фазой сжатия.

Если радиус а круглого преобразователя (точнее – его пьезопластины) значительно меньше расстояния N (что обычно выполняется), то эта разница путей легко вычисляется: ; или ,

где D – диаметр излучателя. Здесь использована формула для приближенного расчета корня. Для прямоугольного преобразователя с отношением сторон не более 2 протяженность ближней зоны приблизительно равна:

,

где S – площадь пьезопластины.

В дальней зоне появление максимумов и минимумов акустического поля под влиянием разницы фаз приходящих волн происходит, когда точка В находится в стороне от оси преобразователя. Амплитуда вдоль оси х уменьшается по закону . Для некоторого расстояния х = r примем амплитуду излучения на оси за 1. Для луча под углом  к оси амплитуда будет равна (). Эту зависимость называют диаграммой направленности.

Угол , при котором  обращается в нуль, определяет угол раскрытия '. Он равен:

,

здесь а – радиус круглого или сторона прямоугольного преобразователя. Для круглого преобразователя n=0,61, а для прямоугольного n=0,5. Обычно считают, что когда амплитуда излучения уменьшается на 10 Дб (амплитуда излучения – приема – на 20 Дб, т.е. в 10 раз), то поле практически отсутствует. Для этого уровня n=0,45 и 0,38 для круглого и прямоугольного преобразователей соответственно. Для прямоугольного преобразователя направленность поля будет разной для каждой из сторон прямоугольника.

На рис. 2.25 показан пример диаграммы направленности в относительных единицах и децибелах. Угол ' ограничивает ее основной лепесток. За его пределами существует несколько боковых лепестков.

Поля излучения, показанные на рис. 2.24,а и 2.25,б сплошными линиями, соответствуют импульсам очень большой длительности. Поля для реально применяемых коротких импульсов показаны штриховыми линиями. Видно, что максимумы и минимумы при этом сглаживаются.

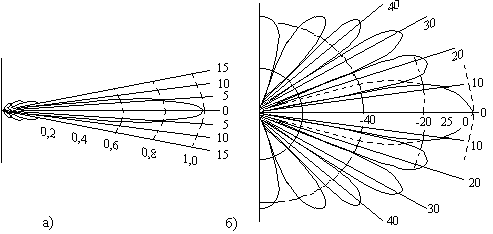
Рис. 2.25. Диаграмма направленности поля излучения для преобразователя с круглой пьезопластиной при отношении диаметра к длине волны 5:

а) – в относительных единицах, б) – в децибелах.

П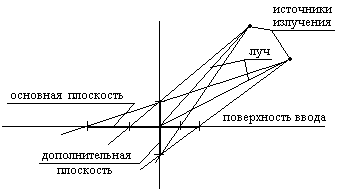 оле наклонного преобразователя рассматривают относительно акустической оси – преломленной геометрической оси пьезопластины. Диаграмма направленности в основной плоскости (плоскости падения) шире, чем в дополнительной плоскости (перпендикулярной плоскости падения и проходящей через акустическую ось), причем расширение тем больше, чем больше угол наклона (рис.2.26). Максимумы и минимумы в ближней зоне не наблюдаются.

Рис. 2.26.