Лекция 8. Цифровые устройства – дешифратор, мультиплексор.
Комбинационное устройство (КУ) - это устройство с m входами и n выходами. Если КУ выполнено на базе идеальных, т.е. безинерционных элементов, состояние выходов однозначно определяется состоянием входов в тот же момент времени. Однако, инерционность элементов и наличие различных факторов, приводящих к задержке распространения сигнала, приводят к задержке появления выходных сигналов КУ, т.е. сигналы на выходе КУ, соответствующие новому состоянию входных сигналов, появляются не сразу, а с некоторой задержкой. При этом в переходный период возможно появление на выходах устройства некоторых промежуточных значений сигналов, не соответствующих заданному состоянию устройства. Такое явление получило название состязаний или гонок. Обычно, вырабатываемые узлами КУ промежуточные значения сигналов, представляют собой импульсы очень малой длительности, являющиеся помехой для всей цифровой системы. Они могут запускать непредусмотренное срабатывание триггеров, счетчиков и осуществлять нежелательные записи в регистры.
Рассмотрим в качестве примера фрагмент схемы комбинационного устройства (рис. 2.1), где может наблюдаться явление гонок. Для наглядности процесса формирования промежуточного значения выходного сигнала приведены временные диаграммы состояний различных цепей распространения в идеальном и реальном случаях (рис.2.2, рис. 2.3).
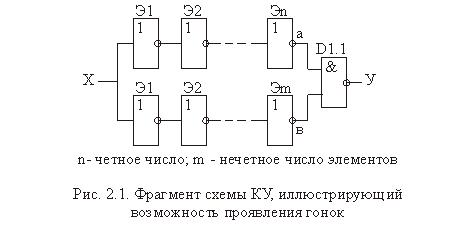
Рис 7.5
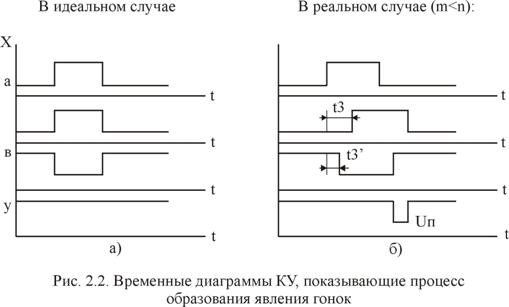
Рис 7.6.
Время задержки импульсов в цепях определяется средним временем задержки распространения сигнала всеми элементами этой цепи. Момент времени появления импульса помехи определяется соотношением числа инвертирующих элементов в конкурирующих цепях фрагмента схемы КУ (см. рис.2.2, а и рис.2.3).
Как следует из рис.2.2, а, если элементы схемы идеальные, т. е. безынерционные, (что на практике достичь не удается), на выходе схемы КУ импульс помехи отсутствует. Однако в реальных схемах всегда имеет место явление гонок и требуется создать такие схемы, в которых влияние этого явления устраняется.
Борьба с гонками. Существует три наиболее часто встречающихся способа борьбы с гонками:
- тактирование;
- построение противогоночных схем;
Рис 7.7.
- учет минимального времени задержки распространения сигнала.
Пример реализации тактирования цикла работы комбинационного устройства (рис.2.4).
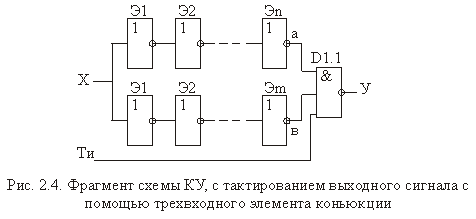
Рис 7.8.
Шифраторы
Шифратор - это логическое устройство, выполняющее преобразование позиционного кода в n разрядный двоичный код. Таким образом, шифратор - это комбинационное устройство, реализующее обратную дешифратору функцию.
Пример шифратора для трех переменных.
Таблица состояния шифратора:
Схема шифратора семиразрядного позиционного кода в трехразрядный двоичный код приведена на рис.7.9. 2.12.
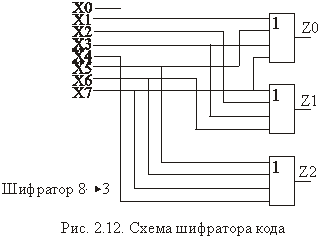
Рис 7.9
Рис 7.10
Дешифратором называется комбинационное устройство, имеющее n входов и m выходов и преобразующее входной код в сигнал в отдельной выходной линии. Другими словами в дешифраторе (декодере) каждому предусмотренному набору входных сигналов соответствует один, вполне определенный, возбужденный выход. Дешифратор называют также преобразователем двоичного (позиционного) кода в унитарный, т.е. содержащий только одну единицу среди нулей (или один нуль среди единиц). Если входной код назвать адресом, то говорят, что декодер преобразует позиционный адрес в физический или пространственный, т.е. указывает своим единственным возбужденным выходом на ту точку пространства, к которой этот код ведет. Дешифратор называется полным, если он имеет столько выходов m, сколько различных комбинаций может иметь n-разрядное двоичное число на его входах, т.е. m = 2n.
Рассмотрим полный дешифратор с n=2 и m=4 с прямыми выходами, т.е. на возбужденном выходе уровень логической 1. Такой дешифратор называют дешифратором по единицам, в отличие от дешифратора по нулям, когда на возбужденном выходе уровень логического 0. Обозначим входы символом х, а выходы – у. Таблица истинности имеет вид:
x1 |
x0 |
y0 |
y1 |
y2 |
y3 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
Запишем структурные формулы для всех выходов:
(8)
Схема дешифратора и его условное обозначение на рис. 23.
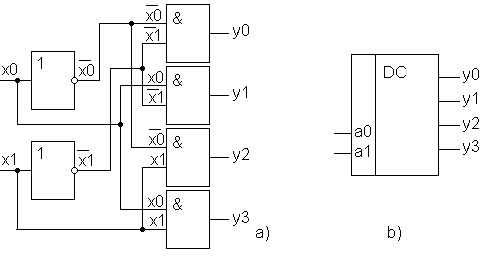
Рис. 7.11. 23. Схема дешифратора (а) и его условное обозначение (b)
Дешифратор по нулям можно построить, исходя из его таблицы истинности, которая строится аналогично дешифратору по единицам, только на активных выходах будут уровни логического 0, и записывая уравнения во второй стандартной форме. В схеме вместо четырех элементов И будут использованы 4 элемента ИЛИ. Таблица истинности дешифратора по нулям полностью инверсна таблице истинности дешифратора по единицам, поэтому его схему можно построить, заменяя в схеме на рис. 23 элементы И на элементы И-НЕ.
Линейный или одноступенчатый дешифратор. Дешифратор - это комбинационное устройство, предназначенное для преобразования параллельного двоичного кода в унитарный, т.е. позиционный код. Обычно, указанный в схеме номер вывода дешифратора соответствует десятичному эквиваленту двоичного кода, подаваемого на вход дешифратора в качестве входных переменных, вернее сказать, что при подаче на вход устройства параллельного двоичного кода на выходе дешифратора появится сигнал на том выходе, номер которого соответствует десятичному эквиваленту двоичного кода. Отсюда следует то, что в любой момент времени выходной сигнал будет иметь место только на одном выходе дешифратора. В зависимости от типа дешифратора, этот сигнал может иметь как уровень логической единицы (при этом на всех остальных выходах уровень логического 0), так и уровень логического 0 (при этом на всех остальных выходах уровень логической 1). В дешифраторах каждой выходной функции соответствует только один минтерм, а количество функций определяется количеством разрядов двоичного числа. Если дешифратор реализует все минтермы входных переменных, то он называется полным дешифратором (в качестве примера неполного дешифратора можно привести дешифратор двоично-десятичных чисел).
Рассмотрим пример синтеза дешифратора (полного) 3 ® 8, следовательно, количество разрядов двоичного числа - 3, количество выходов - 8.
Таблица состояний дешифратора
-
Х3 Х2 Х1
Z0 Z1 Z2 Z3 Z4 Z5 Z6 Z7
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1