Расчет остаточной суммы квадратов

№ опыта	Экспериментальное время остывания заготовки до t = 15 0C, ч	Расчетное время остывания заготовки до t = 15 0C, ч	Погрешность вычисления, ч	Остаточная сумма квадратов
1	9,42	9,87	0,45	0,2
2	24,75	24,75	0	0
3	7,56	7,11	-0,45	0,2
4	20,69	20,69	0	0
5	8,94	8,94	0	0
6	21,92	22,37	0,45	0,2
7	7,14	7,14	0	0
8	19,72	19,27	-0,45	0,2
				0,8

Определим среднее значение расчетного параметра оптимизации по формуле

ч .

Дисперсия результатов расчета по полученной линейной математической модели составит

.

Рассчитаем значение критерия Фишера по формуле

.

Рассчитанное значение критерия Фишера сравним с табличным значением [1] для уровня значимости 0,05 и степеней свободы f₁ = 7 и f₂ = 7.

_{Рассчитанное значение критерия Фишера меньше табличного, следовательно, полученная полиномиальная математическая модель адекватно описывает процесс охлаждения заготовки.}

5.13 Определение погрешности расчета экспериментальной величины по математической модели с учетом взаимодействия факторов

_{Погрешности определения времени остывания заготовки для каждого опыта}

% ;

% ;

% ;

% ;

% ;

% ;

% ;

% .

_{Распределение погрешности аппроксимации приведено на рис. 21.}

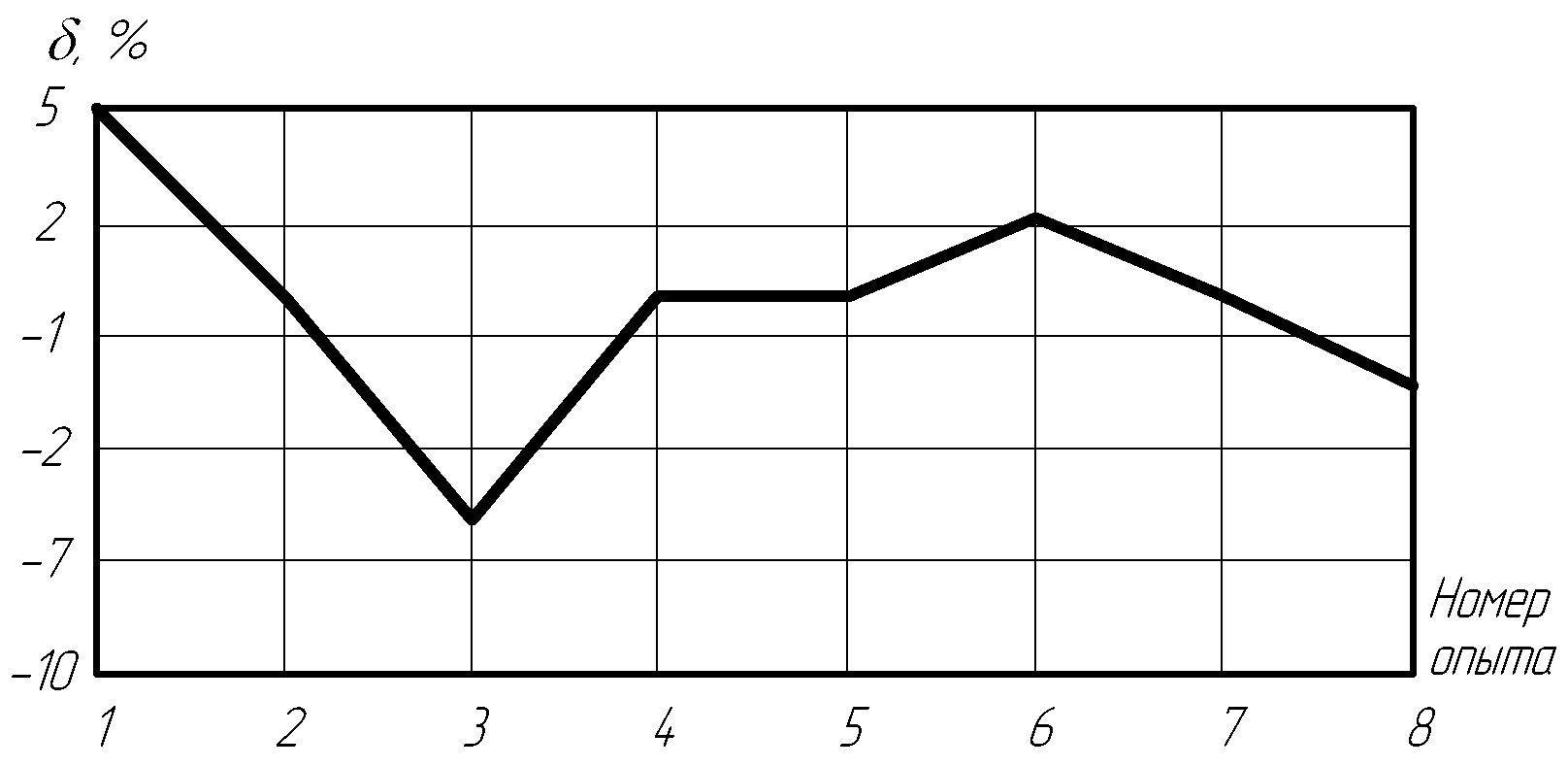
_{Рис. 21 – Распределение погрешности аппроксимации}

_{На рис. 21 видно, что погрешность вычисления времени остывания стальной заготовки при расчете по полученной полиномиальной математической модели находится в пределах от 4,8 % до -6 %.}

_{Средняя погрешность расчета времени остывания заготовки при использовании полиномиальной модели составляет}

_.

_{Следовательно, полученная полиномиальная модель позволяет рассчитать время остывания заготовки с большей точностью.}

5.14 Анализ результатов эксперимента

В приведенном примере выполнено планирование двухуровневого трехфакторного машинного эксперимента и обработаны его результаты.

В приведенном примере выполнено математическое моделирования процесса остывания стальной заготовки в виде цилиндра и получены математические уравнения, связывающие время остывания заготовки и частоту вращения привода вентилятора, площадь наружной поверхности заготовки и ее начальную температуру.

Линейная модель процесса выражается уравнением:

y_Р = 15 – 1,24×х₁ + 6,753×x₂ + 0,588×x₃ .

Анализ уравнений показал, что линейная модель адекватно описывает процесс остывания заготовки с вероятностью 95 %, но имеет низкую точность аппроксимации.

_{Погрешность вычисления времени остывания стальной заготовки при расчете по полученной линейной математической модели находится в пределах от 7,1 % до -9,8 %. Средняя погрешность расчета времени остывания заготовки при использовании линейной модели составляет 3,51%. Следовательно, полученная модель не может быть использована для выполнения точных расчетов.}

Математическая модель процесса остывания с учетом взаимодействия факторов выражается уравнением :

у =15 – 1,24×х₁ + 6,753×x₂ + 0,588×x₃ – 0,325×x₁×x₂ – 0,24×x₁×x₃ +

+ 0,362×x₂×x₃ – 0,225×x₁×x₂×x₃ .

Анализ уравнений показал, что полиномиальная модель адекватно описывает процесс остывания заготовки с вероятностью 95 % и имеет высокую точность аппроксимации.

_{Погрешность вычисления времени остывания находится в пределах от 4,8 % до -6 %. Средняя погрешность расчета времени остывания заготовки при использовании полиномиальной модели составляет 1,88%.}

_{Следовательно, полученная полиномиальная модель отличается большей точностью и может быть использована для выполнения расчетов времени остывания заготовки в области проведения эксперимента или для последующего отыскания оптимума.}