5.9 Проверка адекватности линейной математической модели

Для проверки адекватности выполним расчет времени остывания заготовки по полученной линейной математической модели. Полученные результаты сравним с опытными значениями, рассчитаем погрешность вычисления и остаточную сумму квадратов.

Результаты расчетов представим в виде таблицы 6.

Определим расчетное время остывания заготовки по полученной математической модели.

у_Р1 = 15 – 1,24(- 1) + 6,753(- 1) + 0,5881 = 10,09 ч

у_Р2 = 15 – 1,24(- 1) + 6,7531 + 0,5881 = 23,6 ч

у_Р3 = 15 – 1,241 + 6,753(- 1) + 0,5881 = 7,61 ч

у_Р4 = 15 – 1,241 + 6,7531 + 0,5881 = 21,12 ч

у_Р5 = 15 – 1,24(- 1) + 6,753(- 1) + 0,588(- 1) = 8,92 ч

у_Р6 = 15 – 1,24(- 1) + 6,7531 + 0,588(- 1) = 22,42 ч

у_Р7 = 15 – 1,241 + 6,753(- 1) + 0,588(- 1) = 6,44 ч

у_Р8 = 15 – 1,241 + 6,7531 + 0,588(- 1) = 19,94 ч

Рассчитаем погрешность вычисления.

 у₁ = у_Р1 – у_Э1 = 10,09 - 9,42 = 0,67 ч

 у₂ = у_Р2 – у_Э2 = 23,6 - 24,75 = -1,15 ч

 у₃ = у_Р3 – у_Э3 = 7,61 - 7,56 = 0,05 ч

 у₄ = у_Р4 – у_Э4 = 21,12 - 20,69 = 0,43 ч

 у₅ = у_Р5 – у_Э5 = 8,92 - 8,94 = -0,02 ч

 у₆ = у_Р6 – у_Э6 = 22,42 - 21,92 = 0,5 ч

 у₇ = у_Р7 – у_Э7 = 6,44 - 7,14 = -0,7 ч

 у₈ = у_Р8 – у_Э8 = 19,94 - 19,72 = 0,22 ч

Таблица 6

Расчет остаточной суммы квадратов

№ опыта	Экспериментальное время остывания заготовки до t = 15 0C, ч	Расчетное время остывания заготовки до t = 15 0C, ч	Погрешность вычисления, ч	Остаточная сумма квадратов
1	9,42	10,09	0,67	0,452
2	24,75	23,6	-1,15	1,328
3	7,56	7,61	0,05	0,003
4	20,69	21,12	0,43	0,183
5	8,94	8,92	-0,02	0,001
6	21,92	22,42	0,5	0,253
7	7,14	6,44	-0,7	0,494
8	19,72	19,94	0,22	0,04
				2,762

Проверку соответствия (адекватности) расчета времени остывания заготовки по полученной линейной математической модели экспериментальным данным выполним с помощью критерия Фишера. Для этого рассчитаем дисперсии экспериментально полученного времени остывания заготовки до t = 15 ⁰C и дисперсию времени остывания, рассчитанного по полученной линейной математической модели.

Дисперсию экспериментальных данных рассчитываем по формуле

,

где у_Эi – экспериментальное значение параметра оптимизации; - среднее значение экспериментального параметра оптимизации; N = 8 – количество проведенных опытов.

Параметр f = называют числом степеней свободы рассчитываемой дисперсии.

Дисперсию результатов расчета определяем по формуле

,

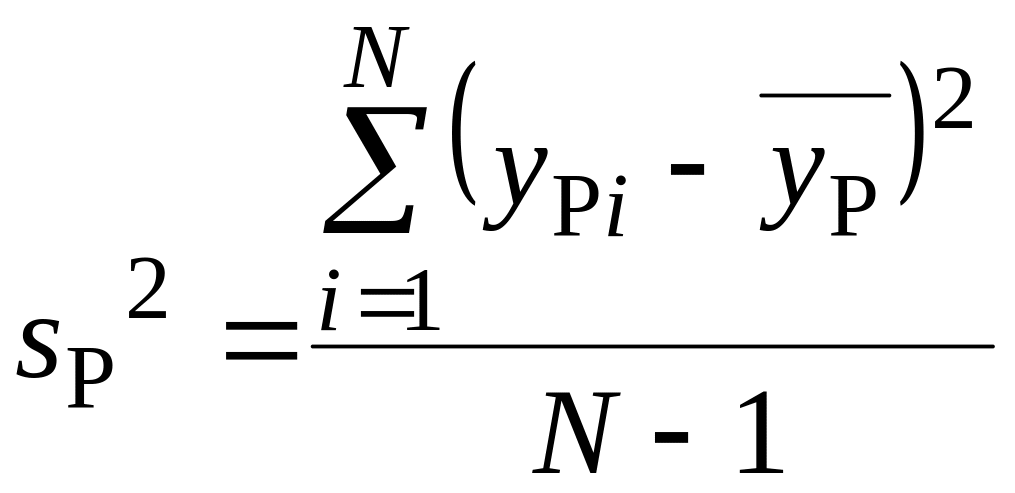где у_Рi – расчетное значение параметра оптимизации; - среднее значение расчетного параметра оптимизации.

Рассчитаем среднее значение экспериментального параметра оптимизации по формуле

ч

Определим среднее значение расчетного параметра оптимизации по формуле

ч

Дисперсия экспериментальных данных составит

.

Дисперсия результатов расчета по полученной линейной математической модели составит

.

_{При сравнении дисперсий по критерию Фишера выдвигаем гипотезу об отсутствии различий между результатами машинного эксперимента и расчетными значениями. Если рассчитанное значение критерия Фишера будет меньше табличного для выбранного уровня значимости, то выдвинутая гипотеза подтверждается и результаты принадлежат к одной генеральной совокупности. Следовательно, полученная формула адекватно описывает происходящий процесс. В противном случае формула не адекватна.}

Рассчитаем значение критерия Фишера по формуле

.

Рассчитанное значение критерия Фишера сравним с табличным значением [1] для уровня значимости 0,05 и степеней свободы f₁ = 7 и f₂ = 7.

_{Рассчитанное значение критерия Фишера оказалось меньше табличного, следовательно, полученная линейная математическая модель адекватно описывает процесс охлаждения заготовки.}