Вентилятора во 14-320 № 5 при новых частотах вращения привода

Объемный расход вентилятора в рабочей точке Р.Т.В составляет V_В = 1,819 м³/с (6,55×10³ м³/ч), в рабочей точке Р.Т.Н - V_Н = 1,264 м³/с (4,55×10³ м³/ч).

Рассчитаем скорость движения воздуха в комнате с остывающей заготовкой.

м/с;

м/с.

Рассчитаем значение критерия Рейнольдса.

;

.

Критерий Нуссельта

;

.

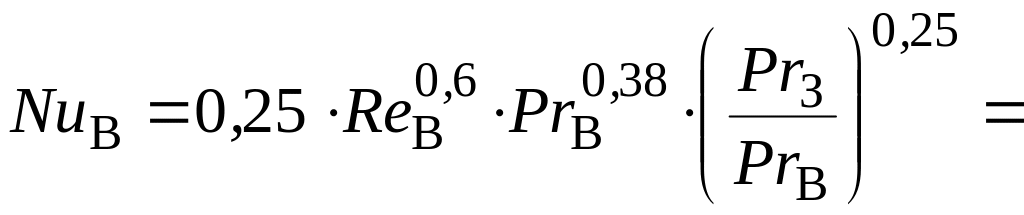
Рассчитаем значения коэффициента теплоотдачи при охлаждении заготовок меньшего диаметра d_Н = 0,142 м.

Вт/м²×К;

Вт/м²×К.

Рассчитаем значения коэффициента теплоотдачи при охлаждении заготовок большего диаметра d_В = 0,234 м.

Вт/м²×К;

Вт/м²×К.

Машинный эксперимент проводим на полученной в разделе 5.4 математической модели остывания заготовки. Исходные данные и результаты полнофакторного машинного эксперимента представим в виде таблицы 5.

Таблица 5

Исходные данные и результаты полнофакторного машинного эксперимента

Номер опыта	Частота вращения привода вентилятора	Площадь наружной поверхности	Начальная температура заготовки	Время остывания заготовки до t = 15 0C
1	1150 об/мин	0,35 м2	525 0С	9,42 ч (3,39104 с)
2	1150 об/мин	0,95 м2	525 0С	24,75 ч (8,91104 с)
3	1650 об/мин	0,35 м2	525 0С	7,56 ч (2,72104 с)
4	1650 об/мин	0,95 м2	525 0С	20,69 ч (7,45104 с)
5	1150 об/мин	0,35 м2	325 0С	8,94 ч (3,22104 с)
6	1150 об/мин	0,95 м2	325 0С	21,92 ч (7,89104 с)
7	1650 об/мин	0,35 м2	325 0С	7,14 ч (2,57104 с)
8	1650 об/мин	0,95 м2	325 0С	19,72 ч (7,1×104 с)

5.8 Математическая модель полного факторного эксперимента

По результатам проведения машинных экспериментов определяются коэффициенты математической модели процесса. Модель полного факторного эксперимента может быть найдена в виде линейной функции

у = b₀ +b₁х₁ + b₂x₂ + b₃x₃

или в виде полинома, учитывающего все возможные сочетания парных взаимодействий факторов и их тройное взаимодействие

у = b₀ +b₁х₁ + b₂x₂ + b₃x₃ + b₁₂x₁x₂ + b₁₃x₁x₃ +

+ b₂₃x₂x₃ + b₁₂₃x₁x₂x₃ .

Коэффициенты в линейной модели вычисляются по формуле

,

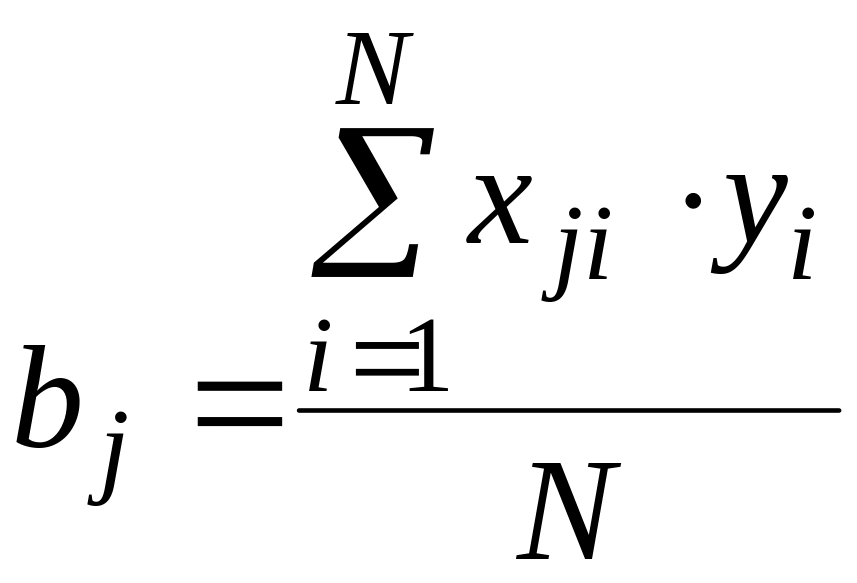где j = 0, 1 , …., k - номер фактора, i = 0, 1 , …., N - номер опыта в соответствии с матрицей планирования эксперимента, y - значение параметра оптимизации.

Коэффициенты при парных взаимодействиях факторов в полиномиальной модели вычисляются по формуле

,

где u, j = 1, 2, . . ., k — номера факторов, u  j.

Коэффициент при тройном взаимодействии факторов в полиномиальной модели вычисляется по формуле

,

где u, j, n = 1, 2, . . ., k — номера факторов, u  j  n.

Рассчитаем значения коэффициентов линейного уравнения.

;

;

;

.

В результате вычисления коэффициентов линейная модель процесса будет иметь вид

y_Р = 15 – 1,24х₁ + 6,753x₂ + 0,588x₃ .