5.2 Выбор параметра оптимизации

Параметр оптимизации должен отвечать следующим требованиям:

1. Он должен быть количественным, то есть за­даваться числом. Мы должны уметь его измерять при любой воз­можной комбинации выбранных уровней факторов. Множество значений, которые может принимать параметр оптимизации, будем называть областью его определения. Области определения могут быть непрерывными и дискретными, ограниченными и неограниченными.

2. Параметр оптимизации должен быть однозначным в статистическом смысле. Заданному набору значений факторов должно соответствовать одно с точностью до ошибки эксперимента значение параметра оптимизации.

3. Параметр оптимизации должен обладать универсальностью или полнотой, то есть всесторонне характеризовать объект исследования.

4. Параметр оптимизации должен иметь физический смысл, быть простым и легко вычисляемым.

В нашем случае параметром оптимизации является время остывания заготовки до температуры t_f = 15 ⁰С.

Время остывания заготовки является количественным параметром и измеряется в секундах или часах.

5.3 Выбор факторов

Фактором называется измеряемая переменная величина, при­нимающая в некоторый момент времени определенное значение.

1. Факторы должны быть управляемыми. Это значит, что экспериментатор, выбрав нужное значение фактора, может его поддерживать постоянным в те­чение всего опыта, т. е. может управлять фактором.

2. Факторы должны быть однозначны. Факторы должны быть непосредственными воздействиями на объект.

В нашем случае факторами являются:

1. Частота вращения привода вентилятора n, об/мин.

2. Площадь наружной поверхности заготовки F_З, м².

3. Начальная температура заготовки t₀, ⁰С.

Все факторы являются управляемыми, их значения могут поддерживаться постоянными в ходе эксперимента, и непосредственно воздействуют на объект.

При проведении эксперимента наружная поверхность заготовки однозначно определяется ее габаритными размерами, измеряемыми с помощью линейки и штангенциркуля, и вычисляется по простым формулам в зависимости от ее формы. Начальная температура заготовки измеряется с помощью термометра и достигается после нагрева заготовки в печи. Различные значения частоты вращения привода вентилятора задаются системой управления частотой вращения приводного двигателя и контролируются с помощью тахометра.

Рассматриваемая совокупность факторов отвечает требованиям совместимости и независимости факторов.

Совместимость факторов означает, что все комбинации их значений осуществимы и безопасны.

Независимость факто­ров определяет возможность установления любого значения фактора вне зависимости от значений других факторов.

5.4 Составление математической модели процесса остывания заготовки

Тепловой баланс заготовки при ее остывании может быть описан уравнением

,

где с_СТ – массовая теплоемкость материала заготовки, Дж/кгК; _СТ – плотность материала заготовки, кг/м³; V_З – объем заготовки, м³; t – фактическая температура заготовки, град;  - время, с;  - коэффициент теплоотдачи, Вт/м²К; F_З – площадь наружной поверхности заготовки, м²; t_f – температура окружающей среды, град.

Начальным условием процесса охлаждения заготовки является равенство фактической температуры заготовки t ее начальной температуре t₀. То есть при  = 0 t = t₀.

Введем величину переменной избыточной температуры

 = t – t_f.

С учетом переменной избыточной температуры уравнение теплового баланса заготовки примет вид

.

В начальный момент времени  = 0 и t = t₀ избыточная температура составит

 = ₀.

Избыточная температура ₀ в начальный момент времени определяется разностью начальной температуры заготовки t₀ после вынимания ее из печи и температуры окружающей среды t_f.

₀ = t₀ – t_f

Решение уравнения уравнение теплового баланса заготовки найдем в виде

.

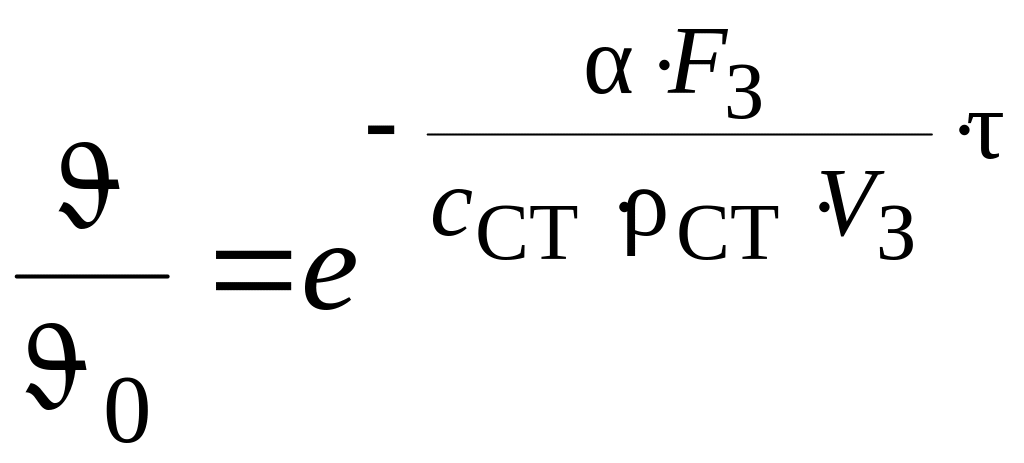Преобразовав последнее уравнение к удобному для вычисления виду, получим зависимость температуры остывающей заготовки от времени

.

Полученное уравнение является математической моделью остывания заготовки. Его решение целесообразно выполнять с использованием вычислительной техники и пакета программ MathCAD 2001 Professional.