Разработка опросных листов (анкет)

Опросный лист для описания потребительских характеристик товара должен включать в себя как можно большее количество анализируемых параметров. Это повышает результативность опроса, однако существенно усложняет работу опрашиваемого и обработку ответов. Поэтому необходим компромисс между объемом информации в анкете и широтой анализа потребительских характеристик.

3. Методы представления и предварительной обработки оценок экспертов

Использование информации, полученной от специалистов, ее сбор, обобщение и анализ с помощью специальных процедур и математических методов получили название методов экспертных оценок.

Рациональное применение этих методов может быть успешным только при условии их приведения в такую форму представления, которая позволит применить для их обработки математические и статистические методы.

В экспертизе участвует несколько экспертов (m), которые оценивают объект (альтернативу, качество, свойство и т.п.) по нескольким факторам (n), получая усредненную оценку (вес) для каждого объекта.

Формализация информации, полученной от экспертов, направлена на устранение ее слабой структурированности, неопределенности, связанной не только с трудностями измерения, но и с самим характером исследуемых целей, средств их достижения и внешних условий.

Какие способы представления мнений экспертов чаще всего применяются на практике? Это:

• Шкальные (интервальные) оценки,

• балльные оценки,

• ранговые оценки (в т.ч. — стандартизированные и нормированные ранги),

• оценки, полученные последовательным сравнением,

• оценки, полученные парным сравнением

Если уровень факторов можно выразить количественно (в рублях, килограммах, процентах), то эксперты могут записать их значения в качестве оценки или преобразовать их по достаточно простым правилам в некоторые шкальные оценки. Например, ввести интервалы с определенным шагом и пронумеровать их (перевод рейтинга в оценки: до 55 –2, 56-65 – 3, 66-80 – 4, больше 80 – 5) ; упорядочить все значения и дать им номер: отлично - 5, хорошо – 4, уд. – 3, неуд - 2 и т.п.

Балльные оценки выставляются каждому фактору в пределах заданной шкалы — 5, 10 или другие. Диапазон значений оценок определяется группой управления исследованиями из таких соображений: чем больше число допустимых оценок, тем точнее выразят свое мнение эксперты, но тем более дорогим и долгим может быть процесс получения и обработки этих ответов.

Характерной особенностью балльных оценок является их взаимная независимость — как в школьных оценках может быть 5 по физкультуре и 2 по физике.

Однако при решении многих практических задач факторы, определяющие конечные результаты, не поддаются количественному измерению, тогда их называют качественными. Например, эффективность создания и внедрения новой техники, или степень влияния (полезности, значимости) какого-либо решения на размер прибыли. Тогда расположение этих факторов в порядке возрастания/убывания составляет отдельную задачу и называется ранжированием. Это требует от экспертом также и сравнения факторов между собой, чтобы «построить» их по ранжиру.

Порядковый метод ранжирования состоит в том, что эксперт располагает объекты (альтернативы) в порядке, который представляется ему наиболее рациональным и приписывает каждому из них порядковый номер – ранг. Он определяется на основе отношений "больше, чем"; "более предпочтителен"; "сильнее" и т.д. При этом ранг 1 получает наиболее предпочтительная альтернатива, а ранг N – наименее предпочтительная. Одно из требований статистики состоит в том, что число n объектов должно быть ровно N, и это означает, что сумма рангов равна сумме натуральных чисел от 1 до n.

Если эксперт не может указать порядок следования для двух или нескольких объектов либо он присваивает разным объектам один и тот же ранг, то в результате число рангов N не равно числу объектов n. В таких случаях объектам приписывают стандартизированные ранги.

Метод последовательных сравнений

Недостаток оценок, получаемых на основе усреднения оценок экспертов, состоит в том, что недостаток качества по одному из факторов можно компенсировать за счет другого, получая один и тот же результат при различной значимости факторов. Поэтому для повышения надежности подобных оценок весьма важное значение имеет выявление связей и установление зависимостей (по возможности количественных) между всеми значимыми факторами.

Для разрешения таких проблем был разработан метод последовательных сравнений (У.Черменом и Р. Акофом) и он состоит в следующем.

Эксперту предоставляется перечень факторов, которые необходимо оценить по их относительной важности и ранжировать.

При этом подходы к сравнительной оценке предлагаются разные.

1 способ. Наиболее важному фактору придается оценка v₁ = 1, а остальным факторам – оценки v_i между 0 и 1 в порядке их относительной важности.

Затем эксперт определяет, является ли фактор с оценкой 1 более важным, чем комбинация остальных факторов. Если это так, то он увеличивает оценку v₁, чтобы она была больше, чем сумма всех остальных, иначе он корректирует v₁ так, чтобы она была меньше суммы всех остальных, то есть в первом случае

а во втором

Далее для V₂ повторяется та же процедура – определяется, является ли второй фактор наиболее важным, чем все остальные факторы, получившие более низкие оценки. Процедура последовательных сравнений продолжается вплоть до (n-1)-го фактора.

Таким образом, используемая здесь процедура состоит в систематической проверке оценок на базе их последовательного сравнения.

Пример. Пусть имеются четыре фактора, определяющие результат некоторого проекта.

Эксперт считает, что их можно упорядочить по степени важности и называет их О1, О2, О3, О4, приписывает им ранги: 1,00; 0,80; 0,50; 0,30 соответственно.

Этот метод становится громоздким, когда число факторов превышает 7. В этом случае предлагается выполнять процедуру в несколько этапов: сначала выделяется примерно средний фактор, все остальные факторы случайным образом разбиваются на 2 или 3 группы (по 5-6-7 факторов). Каждая группа обрабатывается описанным выше способом, а затем по определенному алгоритму эти результаты объединяются². Так получают оценки всех экспертов, а затем составляют матрицу "эксперт/фактор" и переходят к ее обработке.

Метод парных сравнений

Трудности использования ранжирования, непосредственной оценки и метода последовательных сравнений при выявлении предпочтений для большого числа факторов можно в определенной степени уменьшить, если предложить экспертам произвести сравнение факторов попарно, с тем чтобы установить в каждой паре наиболее важный. Будем говорить, что в этом случае эксперт предпочитает данный фактор (хотя не обязательно будет выражать его предпочтение).

В общем случае эксперт может установить равенство объектов или указать свои предпочтения на некоторой шкале.

Производить парное сравнение удобно не только тогда, когда число факторов велико, но и в тех случаях, когда различия между объектами по разным факторам настолько мало, что непосредственное ранжирование не обеспечивают разумного упорядочивания.

Таким образом, метод парных сравнений имеет некоторое преимущество перед другими методами упорядочения в случаях, когда факторов много или они трудно различимы.

Существует два основных подхода определения предпочтений по этому методу.

1. Первый состоит в том, что эксперт ограничивается простой констатацией того, что один фактор предпочтительнее другого – без указания на степень предпочтения. Тогда в матрице парных сравнений в ячейках записываются 0 или 1 – такая матрица известна как "турнирная таблица".

Таблица Пример матрицы парных сравнений одного эксперта

Матрица парных сравнений всегда обратно симметрична относительно главной диагонали, потому что если А1 предпочтительнее, чем А3, т.е. элемент А₁₃ = 1, то А3 менее предпочтителен, чем А1, и А₃₁ = 0. Фактически эксперту нужно заполнять только половину матрицы. Сумма оценок каждого фактора может трактоваться как его ранг. Так что в примере ранги факторов записаны в последнем столбце.

Сначала каждый эксперт заполняет такую матрицу, определяются индивидуальные ранги, а затем они усредняются с учетом мнений всех экспертов. На основе этого строится вторая матрица Р, показывающая процентное отношение случаев, когда фактор i оказывался более значимым, нежели фактор j, в общем числе полученных оценок.

Например, если оценки давали 10 экспертов, то таблица Р, построенная на их оценках, может выглядеть так.

Матрица А: число случаев, когда параметр i определяется

как более важный, чем параметр j

Так как экспертов было 10, то доля предпочтений считается путем деления числа в каждой ячейке таблицы А на число экспертов. В результате имеем таблицу Р.

Матрица Р: доля случаев, когда параметр i определяется

как более важный, чем параметр j

Теперь можно применить простейший прием для ранжирования факторов: разделить суммарную относительную оценку каждого фактора на их сумму, получив нормированную относительную важность каждого фактора, а по ней определить и ранг.

2 способ. Применяется тогда, когда важно определить степень предпочтения одного фактора перед другим. Этот метод охватывает одинаково как те факторы, по которым возможно проведение определенных измерений, так и неосязаемые (качественные) факторы, по которым требуются суждения.

Для проведения субъективных парных сравнений используется шкала, которая оказалась эффективной во многих приложениях, ее правомочность теоретически доказана при сравнении с другими шкалами.

Как и в первом методе, сначала каждый эксперт производит парное сравнение факторов (свойств, последствий решения и т.п.) по предложенной шкале.

Шкала относительной важности

Как и в предыдущем методе, теперь нужно определить приоритеты, или ранги факторов. Это может быть получено любым способом нормирования рангов. Например, применяются следующие методы:

• Эксперты совместно обсуждают свои оценки и в результате принимают единые оценки по каждому фактору, вырабатывая таким образом одну матрицу парных сравнений на всех;

• Эксперты не могут выработать единого мнения, представляют свои таблицы парных сравнений, и на их основе каким-нибудь способом усреднения получают одну таблицу; в качестве способа усреднения могут применяться среднее геометрическое для каждой ячейки, среднее (арифметическое) взвешенное и другие.

При любом подходе получается обобщенная матрица парных сравнений факторов.

На следующем шаге обработки мнений экспертов необходимо оценить степень согласованности их мнений ИС - индекс согласованности.

4. Проверка согласованности и достоверности экспертных оценок

Групповая оценка может считаться достаточно надежной лишь при условии хорошей согласованности ответов опрашиваемых специалистов. Поэтому статистическая обработка информации, полученной от экспертов, должна включать в себя оценку степени согласованности мнений.

Оценки, полученные от экспертов, могут рассматриваться как случайная переменная, распределение которой отражает мнения экспертов о вероятности того или иного выбора события (фактора). Поэтому для анализа разброса и согласованности оценок экспертов применяются обобщенные статистические характеристики – средние и меры разброса:

• средняя квадратичная ошибка,

• вариационный размах min – maх,

• коэффициент вариации V=ср.квадр.откл./ средняя арифм. и т.п.

Для оценки меры сходства мнений каждой пары экспертов могут быть использованы самые разные методы:

коэффициенты ассоциации, с помощью которых учитывается число совпадающих и несовпадающих ответов,

коэффициенты противоречивости мнений экспертов,

коэффициенты ранговой корреляции Кендалла и Спирмена.

Все эти меры можно использовать либо для сравнения мнений двух экспертов, либо для анализа связи между рядами оценок по двум признакам.

Коэффициент корреляции рангов Спирмена:

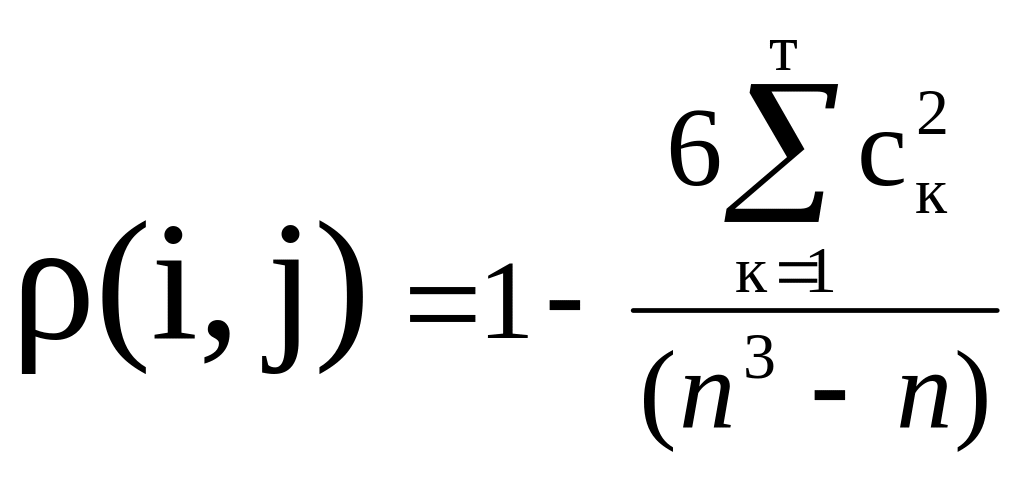
где n – число экспертов,

c_k – разность оценок i-го и j-го экспертов по всем T факторам.

В практике экспертных оценок, однако, часто приходится сопоставлять много признаков. В таких случаях попарное сравнение комбинации факторов (например, по Спирмену) может оказаться чрезвычайно трудоемким, поэтому были разработаны специальные критерии, позволяющие относительно просто оценить согласованность мнений экспертов по ряду факторов.

Конкордация

Согласованность мнений по нескольким факторам оценивается с помощью коэффициента конкордации W, то есть общего коэффициента ранговой корреляции для группы, состоящей из m экспертов.

Доказано, что величина S, когда все эксперты дают одинаковые оценки по всем факторам, имеет максимальное значение, равное

где n – число факторов,

m – количество экспертов.

Однако, на практике такое событие невероятно, поэтому согласованность (коэффициент конкордации W) определяется как отношение фактической меры согласованности S к S_max :

W = S/S_max , или

Формула для расчета S приведена ниже:

,

где обозначения те же, что выше.

Рассмотрим процесс определения коэффициента конкордации на примере ранговых оценок, выданных 7-ю экспертами по 6-ти факторам (табл. ниже )

Для расчета сначала находится сумма оценок (рангов) по каждому фактору, полученная от всех экспертов, затем их средняя арифметическая, отклонения суммарной оценки фактора от средней и сумма их квадратов:

В нашем случае S_max = 1/12*6*49*(36 - 1) = 857,5, а S = 743,5

Коэффициент конкордации равен отношению W= S / S_max, , причем если W близок к 1, то все эксперты дали примерно одинаковые оценки, их мнения достаточно согласованны.

W = S/S_max = 743.5 / 857,5 = 0,87

Согласованность мнений экспертов высокая.

Еще раз хотелось бы подчеркнуть, что приведенные формулы пригодны только при строгом ранжировании (как в примере — у каждого эксперта все оценки попарно разные).

Список использованных источников по теме:

1. Саати Т., Кернс К. Аналитическое планирование: Организация систем : Пер. с англ. — М.: Радио и связь, 1991. — 224 с.

2. Саати Т. Принятие решений. Метод анализа иерархий. — М.: Радио и связь, 1993. — 320 с.

3. Таха Х. А. Введение в исследование операций, 6-е издание : Пер. с англ. — М.: Издательский дом «Вильямс», 2001. — 912 с.

4. Блюмин С.Л., Шуйкова И.А. Введение в математические методы принятия решений. — Липецк: ЛГПИ, 1999

5. Карлберг К Бизнес-анализ с помощью Excel 2000.: Пер. с англ.: Уч. пособие. – М.: Изд. Дом “Вильямс”, 2000. – 480 с.

6. Берк К, Кэйри П. Анализ данных с помощью Microsoft Excel: пер. с англ. – М.: Издательский дом «Вильямс», 2005. – 560 с.: ил.

7. Бешелев С. Математико-статистические методы экспертных оценок, 1980

Методы принятия решений в условиях неопределенности и риска

Постановка задачи

Чтобы найти хорошее решение, следует:

1. Определить цель решения.

2. Определить возможные варианты решения проблемы.

3. Определить возможные исходы каждого решения.

4. Оценить каждый исход.

5. Выбрать оптимальное решение на основе поставленной цели.

Как видим, поиск решения начинается с перечисления возможных вариантов и их исходов, затем производится оценка каждого исхода. Такова схема рассуждений при проведении количественного анализа. Вышеперечисленные этапы важны как в очень сложных случаях, так и в очень простых.

Рассмотрим лишь некоторые из возможных целей принятия решений, но в любом случае выбор "лучшего варианта" зависит от обстоятельств и точки зрения того, кто принимает решение.

Пример 1. Отдел маркетинга компании "Singles pic" представил своему руководству данные об ожидаемом объеме сбыта программных продуктов при трех вариантах цены.

Таблица 1. Предполагаемые объемы продаж программных продуктов по разным ценам, руб.

Постоянные затраты составляют 40000 руб. в год, переменные — 4,00 руб. на единицу.

Решение состоит в том, чтобы назначить оптимальную цену. Заметим, у нас имеется всего лишь три варианта цены, т.е. только три возможных решения, и, чтобы облегчить расчеты, для каждого из вариантов по три исхода — различные объемы продаж.

Решение.

Для каждого исхода рассчитаем доход. В данном случае доход — это годовая прибыль.

Для того чтобы объяснить, какие трудности возникают в результате неопределенности, мы будем использовать данные из этой таблицы. Можно представить убедительные аргументы, которые приведут нас к одному из трех возможных решений.

Наибольшая прибыль для наиболее вероятного объема продаж равна 57600 руб. Эта цифра будет получена, если назначить цену в 8,80 руб. Однако цена 8,60 руб. предпочтительнее для компании, так как наиболее вероятная прибыль составляет примерно ту же величину, в то время как прибыль двух остальных исходов выше, чем для цены 8,80 руб.

Однако если мы примем во внимание постоянные расходы, то цена 8,00 руб. — единственная, при которой "Singles" не терпит убытков, так как низкая прибыль здесь не меньше, чем постоянные расходы — 40000 ф. ст.

Таким образом, для любого из трех решений существуют свои аргументы.

Какое решение будет принято, зависит от целей, которые оно преследует, и от отношения к риску - того, кто принимает решение:

Осторожный менеджер предпочтет цену 8,00 руб. двум другим: возможные прибыли меньше, но и потери сведены к минимуму. Поэтому в числе прочих должен решаться вопрос об отношении к риску. Сейчас мы рассмотрим, как правила принятия решений могут применяться в каждом конкретном случае, а к вопросу о риске вернемся позже.

ПРАВИЛА ПРИНЯТИЯ РЕШЕНИЙ

Как уже отмечалось, принимая решения, следует руководствоваться соответствую­щими правилами. Принимающий решение сам выбирает, каким правилом ему воспользоваться, потому что для каждого случая применимо какое-то определенное правило.

Итак, они делятся на две группы:

— правила принятия решений без использования численных значений вероят­ностей исходов;

— правила принятия решений с использованием численных значений вероят­ностей исходов.

Правила принятия решений без использования численных значений вероятностей исходов:

1. Максимаксное решение — максимизация максимума доходов.

2. Максиминное решение — максимизация минимума доходов.

3. Минимаксное решение — минимизация максимума возможных потерь.

Пример ^2. Предположим, что вы владелец кондитерской "Cake Box". В начале каждого дня вам нужно решить вопрос, сколько пирожных следует иметь в запасе, чтобы удовлетворить спрос. Каждое пирожное обходится вам в 0,70 д.е, а вы его продаете по 1,30 д.е.. Продать невостребованные пирожные на следую­щий день невозможно, поэтому остаток распродается в конце дня по 0,30 д.е. за штуку. Нужно определить, сколько пирожных должно быть закуплено в начале каждого дня. В табл. 3 приведены данные по продажам в предыдущие периоды.

Таблица 3.3. Спрос на пирожные

Решение.

Итак, в начале дня можно закупить для последующей продажи 1, 2, 3, 4 или 5 пирожных в день.

В общем решение и его исходы примерно равны, но имея возможность принимать решения, нельзя контролировать исходы. Покупатели определяют их сами, поэтому исходы представляют также "фактор неопределенности". Чтобы определить вероятность каждого исхода, составим список возможных решений и соответствующих им исходов. В табл. 4 рассчитаны доходы, иначе говоря, отдача в денежном выражении для любой комбинации решений и исходе:

Таблица 4 Доход (прибыль) в день, д.е.

Используя каждое из правил принятия решений, нужно ответить на вопрос: "Сколько пирожных должна закупить фирма "Cake Box" в начале каждого дня?"

1. Правило максимакса — максимизация максимума доходов (оптимистичный подход). Каждому возможному решению в нижней строке таблицы соответствуют максимальные доходы. По этому правилу вы закупите в начале дня пять пирожных. Это подход карточного игрока — игнорируя возможные потери, рассчитывать на максимально возможный доход.

Таблица 5. Максимальные доходы

2. Правило максимина — максимизация минимального дохода (осторожный подход). Каждому возмож­ному решению в верхней строке таблицы соответствуют минимальные доходы (табл. 6). По этому правилу вы закупите в начале дня одно пирожное, чтобы максимизи­ровать минимальный доход. Это очень осторожный подход к принятию решений.

Таблица 6. Минимальные доходы

3. Правило минимакса — минимизация максимально возможных потерь (пессимистический подход). В данном случае больше внимания уделяется возможным потерям, чем доходам. Таблица возможных потерь дает представление о прибылях каждого исхода, потерянных в результате принятия неправильного решения.

Например, если спрос составляет два пирожных и было закуплено два, то доход составит 1,20 д.е., если же вы приобрели три, то доход — 0,80 д.е. и вы недополучили 0,40 д.е (вместо 0,70 получили 0,30). Эти 0,40 д.е. — то, что называется возможными потерями или упущенным доходом. Таблицу возможных потерь можно получить из таблицы доходов, находя наибольший доход для каждого исхода и сопоставляя его с другими доходами этого же исхода (см. табл. 7).

Как уже отмечалось, правило, которое используется для работы с таблицей упущенных доходов, — это правило минимакса. Оно также называется минимакс­ное правило возможных потерь. Состоит оно в том, чтобы для каждого решения выбрать максимально возможные потери. Затем выбирается то решение, которое ведет к минимальному значению максимальных потерь (табл. 8).

Таблица 7. Возможные потери в день, д.е.

Таблица 8 Максимальные возможные потери

Минимальная величина максимальных потерь возникает в результате закупки трех или четырех пирожных в день. Следовательно, по правилу минимакса вы выберете одно из этих решений.

Все рассмотренные критерии принятия решений приводят к различным ре­зультатам. Поэтому сначала выбирается тот критерий, который считается "луч­шим", и тогда вы получаете "наилучшее" для вас решение.

Правила принятия решений с использованием численных значений вероятностей исходов

В предыдущем разделе мы не использовали данные о вероятностях исходов, теперь попробуем при принятии решений использовать эти данные.

1. Правило максимальной вероятности — максимизация наиболее вероятных доходов. Рассмотрим относительные частоты (вероятности) дневного спроса на пирожные. В табл. 10 приведены данные по продажам в предыдущие периоды.

Таблица 10 Спрос на пирожные

Наибольшая вероятность 0,3 соответствует спросу в три и четыре пирожных в день. Теперь рассмотрим доходы каждого из исходов и выберем наибольший.

Таблица 11. Максимальный доход для каждого из решений

По этому правилу фирма "Cake Box" должна закупать четыре пирожных в день.

"ДЕРЕВО" РЕШЕНИЙ

Примеры, которые мы рассматривали до сих пор, включали в себя единственное решение. Однако на практике результат одного решения заставляет нас принимать следующее и т.д. Эту последовательность нельзя выразить таблицей доходов, поэтому нужно использовать какой-то другой процесс принятия решений.

Схема "дерево" решений очень похожа на схему "дерево" вероятностей. Ее используют, когда нужно принять несколько решений в условиях неопределенности, когда каждое решение зависит от исхода предыдущего или исходов испытаний. Состав­ляя "дерево" решений, нужно нарисовать "ствол" и "ветви", отображающие структуру проблемы. Располагаются "деревья" слева направо. "Ветви" обозначают возможные альтернативные решения, которые могут быть приняты, и возможные исходы, возни­кающие в результате этих решений. На схеме мы используем два вида "ветвей": первый — пунктирные линии, соединяющие квадраты возможных решений, второй — сплош­ные линии, соединяющие кружки возможных исходов.

Квадратные "узлы" обозначают места, где принимается решение,

круглые "узлы" — появление исходов.

Так как принимающий решение не может влиять на появление исходов, ему остается лишь вычислять вероятность их появления.

Когда все решения и их исходы указаны на "дереве", просчитывается каждый из вариантов, и в конце проставляется его денежный доход. Все расходы, вызван­ные решением, проставляются на соответствующей "ветви".

Пример 5. Для финансирования проекта бизнесмену нужно занять сроком на один год 15000 $. Банк может одолжить ему эти деньги под 15% годовых или вложить в дело со 100%-ным возвратом суммы, но под 9% годовых. Из прошлого опыта банкиру известно, что 4% таких клиентов ссуду не возвращают. Что делать? Давать ему заем или нет? Перед вами пример задачи с одним решением, поэтому можно воспользоваться как таблицей доходов, так и "деревом". Рассмотрим оба варианта.

Решение 1 (по таблице доходов).

Максимизируем ожидаемый в конце года чистый доход, который представляет собой разность суммы, полученной в конце года, и инвестированной в его начале. Таким образом, если заем был выдан и возвращен, то чистый доход составит:

Чистый доход = ((15000 + 15% * 15000) - 15000) = 2250$

Таблица 3.23. Чистый доход в конце года, $.

Если банк решает выдать заем, то максимальный ожидаемый чистый доход равен 1560 $.

Решение 2 (по "дереву" решений).

В данном случае также используем критерий максимизации ожидаемого в конце года чистого дохода.

Далее расчет ведется аналогично расчетам по таблице доходов. Ожидаемый чистый доход в кружках А и В вычисляется следующим образом:

В кружке А:

Е (давать заем) = {17250 * 0,96 + 0* 0,04} - 15000 = 16500 - 15000 = 1560 $.

В кружке В:

Е (не давать заем) = {16350 * 1,0 - 15000} = 1350 $.

Поскольку ожидаемый чистый доход больше в кружке А, то принимается решение выдать заем.

Расчет двухуровневого "дерева" решений

Пример 3.6. Рассмотрим ситуацию более сложную, чем в предыдущем примере, а именно: банк решает вопрос, проверять ли конкурентоспособность клиента перед тем, как выдавать заем. Аудиторская фирма берет с банка 80 ф. ст. за каждую проверку. В результате этого перед банком встают две проблемы: первая — проводить или нет проверку, вторая — выдавать после этого заем или нет.

Решая первую проблему, банк проверяет правильность выдаваемых аудитор­ской фирмой сведений. Для этого выбираются 1000 человек, которые были проверены и которым впоследствии выдавались ссуды:

Таблица 3.24. Рекомендация аудиторской фирмы и возврат ссуды

Какое решение должен принять банк?

Решение.

Этап 1. Построим "дерево", как показано ниже. Вероятности проставляются по данным этапа 2.

Этап 2. Используя данные табл. 3.24, вычислим вероятность каждого исхода:

Р (клиент ссуду вернет; фирма рекомендовала) = 7,35/750 = 0,98;

Р (клиент ссуду не вернет; фирма рекомендовала) = 15/750 = 0,02;

Р (клиент ссуду вернет; фирма не рекомендовала) = 225/250 = 0,9;

Р (клиент ссуду не вернет; фирма не рекомендовала)= 25/250= 0,1.

Этап 3. На этом этапе слева направо проставим денежные исходы каждого из "узлов", используя конечные результаты, вычисленные ранее. Любые встречаю­щиеся расходы вычитаем из ожидаемых доходов. Таким образом, подсчитываем все "дерево", опираясь на ранее полученные результаты. После того, как пройдены квадраты "решений", выбирается "ветвь", ведущая к наибольшему из возможных при данном решении ожидаемому доходу. Другая "ветвь" зачеркивается, а ожи­даемый доход проставляется над квадратом решения.

Сначала посмотрим на кружки исходов В и С, являющиеся следствием квад­рата 2 (выдавать ли заем клиенту?)

Доход, ожидаемый от исхода В:

Е (В) = 17250 ф. ст. * 0,98 + 0 * 0,02 = 16905 ф. ст.,

чистый ожидаемый доход:

NE (В) = 16905 - 15000 = 1905 ф. ст.

Доход, ожидаемый от исхода С:

Е (С) = 16350 ф. ст. х 1,0 = 16350 ф. ст.,

чистый ожидаемый доход:

NE (С) = 16350 - 15000 = 1350 ф. ст.

Принятие решений в условиях определенности

Задачи линейного программирования

Инструментом моделирования распределения ресурсов для достижения цели чаще всего являются методы линейного программирования.

Задача линейного программирования является частным случаем задачи оптимизации и записывается в следующем виде:

Задачу линейного программирования можно решать графическими и аналитическими методами. Одним из самых известных аналитических методов по праву считается симплекс-метод, который реализован в Excel (симплексом тела в k-мерном пространстве называют совокупность k+1 его вершин). Алгоритм симплекс-метода обеспечивает переход от одной вершины к другой в таком направлении, при котором значение целевой функции от вершины к вершине улучшается. Поэтому и аналитический метод, основанный на итерациях вычисления целевой функции и переменных в вершинах, с учетом этого получил свое название.

Рассмотрим сам метод, его реализацию в Excel и, самое главное, анализ результатов с целью принятия решений на примере, приведенном в книге³ задачи распределения ресурсов.

З адача. Требуется определить, в каком количестве надо выпускать продукцию типов Прод1, Прод2, Прод3, Прод4 с целью получения наибольшей прибыли. Известно, что для изготовления требуются ресурсы трех видов: трудовые, сырье, финансы. Количество каждого ресурса на момент решения задачи, норма расхода каждого вида ресурса на единицу продукции каждого типа и прибыль от реализации единицы продукции известны и приведены в таблице на рис. 1.

Рис.1

Введем обозначения:

x_j – количество выпускаемой продукции j-го типа (j= 1…4);

b_i – количество наличного ресурса i-го вида (i= 1…3);

a_ij – норма расхода i-го ресурса для выпуска единицы продукции j-го типа;

c_j – прибыль, получаемая от реализации единицы продукции j-го типа.

Математическая модель задачи имеет вид:

F == 60x₁ +70x₂ + 120x₃ +130x₄ Þ max

x₁ + x₂ + x₃ + x₄ <= 16

6x₁ +5x₂ +4x₃ + 3x₄ <= 110

4x₁ + 6x₂ +10x₃ + 13x₄ <= 100

x_ij >=0, j = 1…4

Вычисление всех искомых значений обеспечивает Excel с помощью надстройки Сервис–Поиск решения.

1. Решение Задачи линейного программирования с помощью Excel

Ввод условий задачи состоит из следующих шагов:

• Создание формы для ввода условий задачи,

• Ввод исходных данных,

• Ввод зависимостей из математической модели,

• Назначение целевой функции,

• ввод ограничений и граничных условий.

Рассмотрим эти шаги на примере задачи распределения ресурсов, для которой уже построена математическая модель.

1. Создадим форму ввода,

2. Заполним ячейки значениями коэффициентов целевой функции (строка 6),

3. Введем нормы расхода сырья в ячейки В10:Е12

4. В столбце F запишем формулы целевой функции и левых частей ограничений,

5. Введем ограничения ресурсов в столбец Н.

Примечание. Формулы записываются с применением функции СУММПРОИЗВ()

Получим рис. 2.

Рис. 2

Диалоговое окно Поиска решения

1. Установить целевую ячейку F6

2. Равной максимальному значению

3. Изменяя ячейки В3:Е3

4. Ограничения F10 <= H10 и т.д.

5. Выполнить

Параметры:

Предельное число итераций – 100

Линейная модель – применяется симплекс-метод

Возможные сообщения:

• "Поиск не может найти подходящего решения";

нужно корректировать модель исходных данных

• "Значения целевой ячейки не сходятся";

нужно ввести дополнительные ограничения

• "Решение найдено"

нужно получить отчет и провести анализ.

Анализ оптимального решения

Если решение найдено, то в диалоговом окне можно вызвать отчеты трех типов:

• результаты,

• устойчивость,

• пределы.

Отчет получаем на новом листе, ярлычок которого содержит название отчета.

Отчет по результатам:

Отчет состоит из трех таблиц:

• Таблица 1 приводит сведения о целевой функции.

• Таблица 2 содержит значения искомых переменных (оптимальное решение).

• Таблица 3 показывает результаты оптимального решения для ограничений и граничных условий, а именно:

• Для ограничений ресурсов приведены Значения, которые показывают, сколько данного ресурса будет использовано, и Разница, где подсчитано количество неиспользованного ресурса. Если ресурс использован полностью, то в графе Состояние записано "связанное", иначе – "не связан"

• Для граничных условий, которые накладывались на значения переменных (в большинстве случаев это условие неотрицательности), приводятся аналогичные величины, только в данном случае Разница показывает отличие значения переменной для оптимального решения от первоначального значения в ячейке (как правило, там 0).

Сведения о ППС

1 По материалам книги Бешелев С.Д., Гурвич Ф.Г. Математико-статистические методы экспертных оценок. – 2-е изд. – М.: Статистика, 1980. – 263 с.

2 Бешелев С., Гурвич Ф. Математико-статистические методы экспертных оценок. М.: Статистика, 1980 г.

3 Курицкий Б. Поиск оптимальных решений средствами Excel 7.0. – СПб.: BHV -Санкт-Петербург, 1997