3. Перевірка статистичних гіпотез

Статистичною гіпотезою називають деяке твердження щодо значення (або значень) якого-небудь параметра випадкової величини. Наприклад, твердження M(Х)=5 (гіпотеза про те, що математичне сподівання дорівнює п'яти) або твердження D(Х)=D(Y) (гіпотеза про рівність двох дисперсій).

Під процедурою перевірки статистичних гіпотез розуміють послідовність дій, які дозволяють з тією або іншою мірою достовірності підтвердити або спростувати гіпотезу.

Формалізація статистичних гіпотез з математичної точки зору приводить до описання гіпотез двох видів:

Н₀ – нульова гіпотеза,

Н₁ – аль­тернативна гіпотеза.

Нульова гіпотеза (Н₀) формулюється як гіпотеза про відсутність відмінностей у вибірках, про схожість двох розподілів і тому подібне. Альтернативна гіпотеза (Н₁) протилежна за смислом і означає відмінність у вибірках, відмінність двох розподілів і тому подібне. Дві гіпотези утворюють повну групу несумісних подій: якщо приймається одна, то інша відхиляється.

Гіпотези перевіряються за допомогою статистичних критеріїв.

Статистичний критерій – це правило, яке дозволяє приймати істинну і відхиляти помилкову гіпотезу з високою ймовірністю. Математично критерій є формулою, результатом розрахунків за якою є деяке число. Критерій є випадковою величиною, розподіл якої залежить від числа ступенів свободи.

Для встановлення схожості-відмінності середніх арифметичних значень в двох вибірках (які вибираються з генеральних сукупностей, що мають нормальний розподіл) використовується t-критерий Стьюдента:

,

(15)

де: s² – виправлена вибіркова дисперсія,

n₁ – об’єм першої вибірки;

n₂ – об’єм другої вибірки.

Інший варіант формули:

,

(16)

де: ² – зміщена вибіркова дисперсія.

Розраховане за наведеними формулами емпіричне значення критерію Стьюдента зрівнюється з критичним значенням цього критерію. Критичне значення критерію Стьюдента вибирається з відповідної таблиці (див. Додаток Б) залежно від рівня значущості  (0,05; 0,01; 0,001) та кількості ступенів свободи f (f = n₁ + n₂ - 2).

Якщо емпіричне значення критерію Стьюдента не перевищує його критичного значення, то приймається нульова гіпотеза про відсутність статистично значимих відмінностей середніх арифметичних значень в двох вибірках. У протилежному випадку нульова гіпотеза відхиляється.

Для встановлення схожості-відмінності дисперсій в двох незалежних вибірках (які витягують з генеральних сукупностей, що мають нормальний розподіл) використовується критерій Фішера:

,

(17)

де: – більша дисперсія,

– менша дисперсія.

Розраховане за наведеною формулою емпіричне значення критерію Фішера зрівнюється з критичним значенням цього критерію. Критичне значення критерію Фішера вибирається з відповідної таблиці (див. Додаток В) залежно від рівня значимості  (0,05; 0,01; 0,001) і кількості ступенів свободи. Кількість ступенів свободи визначається окремо для чисельника та знаменника за формулами:

f1 = n1 - 1, f2 = n2 - 1,

(18)

де: n₁ – об’єм вибірки з більшою дисперсією,

n₂ – об’єм вибірки з меншою дисперсією.

Якщо емпіричне значення критерію Фішера не перевищує його критичного значення, то приймається нульова гіпотеза про відсутність статистично значимих відмінностей дисперсій в двох вибірках. У протилежному випадку нульова гіпотеза відхиляється.

Зауважимо що рівень значущості  характеризує ймовірність помилки відхилити істинну гіпотезу.

Приклад 2. У двох друкарських цехах були проведені заходи щодо підвищення якості продукції. У кожному цеху використовувалася своя методика підвищення якості. До проведення заходів в обох цехах мало місце однакове розсіювання (розкид) параметрів видання. Після проведення заходів в кожному цеху здійснені вибіркові дослідження формату видання, результати яких представлені в таблиці 4.

Визначити, чи дійсно методика, використана в 1 цеху, дала найбільше вирівнювання параметрів видань (взяти рівень значущості =0,05).

Таблиця 4

Результати дослідження формату видання,

отримані в двох цехах

Показник	1 цех	2 цех
кількість перевірених екземплярів видання	21	16
вибіркова дисперсія	0,16 (мм)	0,36 (мм)

Для розв’язання цієї задачі розрахуємо емпіричне значення критерію Фішера:

F = = 0,36/0,16 = 2,25,

де: – дисперсія формату видання в 1 цеху,

– дисперсія формату видання в 2 цеху.

Кількість ступнів свободи:

f₁=20,

f₂=15.

Критичне значення критерію Фішера знайдемо по таблиці, наведеної в Додатку В (для =0,05):

F_к= 2,203.

Оскільки F > F_к, то ми робимо висновок про наявність статистично значимих відмінностей дисперсій в 1 і 2 цеху. Отже, методика, використана в 1 цеху, оказала більший вплив на стабілізацію технологічного процесу.

ЗАВДАННЯ

Завдання 1

Відповісти на запитання:

До якого типу випадкових величин – неперервного чи дискретного – належить ширина поля в книзі?

Який тип розподілу має ця випадкова величина?

До якого типу випадкових величин – неперервного чи дискретного – належить кількість бракованих виробів в партії?

Завдання 2.1

Випадкова величина ξ розподілена за нормальним законом. Знайти надійний інтервал для математичного сподівання з надійністю 0,95, враховуючи, що вибіркове середнє дорівнює 0,9; середнє квадратичне відхилення дорівнює 1; об'єм вибірки – 64.

Завдання 2.2

Випадкова величина ξ розподілена за нормальним законом. Знайти надійний інтервал для оцінки невідомого математичного сподівання за значенням вибіркового середнього . Початкові дані для розрахунків за варіантами наведені в табл. 5.

Таблиця 5

Початкові дані для розрахунків за варіантами

	Номер варіанту
Показники	1	2	3	4	5	6	7	8	9
n	36	30	40	50	60	70	80	90	100
	0,95	0,95	0,97	0,874	0,986	0,994	0,984	0,98	0,796
	3	1	2	3	4	5	6	7	8
	10	20	30	40	50	60	70	80	90

Позначення в таблиці:

n – об'єм вибірки;

 – надійність (довірча ймовірність);

– вибіркове середнє;

 – середнє квадратичне відхилення.

Завдання 2.3

Виконати завдання 2.2 для різних значень надійності: 0,95; 0,96; 0,97; 0,98; 0,99.

Завдання 2.4

З метою визначення середньої ваги видання на підприємстві методом випадкової вибірки проведено обстеження 400 екземплярів даного видання. Середня за вибіркою вага дорівнює 200 г. Вважаючи, що вага видання має нормальний закон розподілу, визначити із заданою вірогідністю межі, в яких опиниться середня вага для всієї генеральної сукупності екземплярів, якщо відомо, що σ = 1,7 г.

Значення надійної ймовірності наведені у табл. 6.

Таблиця 6

Значення надійної ймовірності за варіантами

Номер варіанту	
1	0,95
2	0,96
3	0,97
4	0,874
5	0,986
6	0,994
7	0,984
8	0,98
9	0,796

Завдання 3.1

Кількісна ознака ξ генеральній сукупності розподілена нормально. Для вибірки об'ємом n=16 знайдене вибіркове середнє =20,2 та виправлене середнє квадратичне відхилення s=0,8. Оцінити невідоме математичне сподівання m за допомогою надійного інтервалу з надійністю =0,95.

Завдання 3.2

З метою визначення середньої тривалості робочого дня на поліграфічному підприємстві методом випадкової вибірки проведено обстеження тривалості робочого дня співробітників. Зі всього колективу заводу випадковим чином вибрано 30 співробітників. Відомості табельного обліку про тривалість робочого дня цих співробітників і склали вибірку. Середня за вибіркою тривалість робочого дня дорівнює 6,85 години, а виправлене середнє квадратичне відхилення S = 0,7 години. Вважаючи, що тривалість робочого дня має нормальний закон розподілу, з надійністю  = 0,95 визначити, у яких межах знаходиться істинна середня тривалість робочого дня для всього колективу досліджуваного підприємства.

Завдання 4

У двох друкарських цехах були проведені заходи щодо підвищення якості продукції. У кожному цеху використовувалася своя методика підвищення якості. До проведення заходів в обох цехах мав місце однаковий рівень якості (якість оцінювалася в балах за 150-бальною шкалою). За підсумками заходів в кожному цеху проведені вибіркові дослідження рівня якості продукції, результати яких представлені в табл. 7.

Таблиця 7

Результати дослідження рівня якості продукції,

отримані в двох цехах

Показники	1 цех	2 цех
кількість перевірених екземплярів видання	30	32
вибіркова середнє	103	110
вибіркове середнє квадратичне відхилення	10	12

Визначити, чи дійсно методика, використана в 2 цеху, забезпечила вищий рівень якості друкарської продукції (розглянути різні рівні значимості).

Завдання 5

5.1. Вивчити призначення функції ДОВЕРИТ в Excel. Які з попередніх завдань можна розв’язати з її допомогою? Застосувати функцію ДОВЕРИТ для виконання цих завдань.

5.2. Вивчити призначення функції СТЬЮДРАСПОБР в Excel. Яке з попередніх завдань можна розв’язати з її допомогою? Застосувати функцію СТЬЮДРАСПОБР для виконання цього завдання.

5.3. Вивчити призначення функції FРАСПОБР в Excel. Застосувати цю функцію для виконання Прикладу №2, наведеного у навчальному матеріалі даної лабораторної роботи.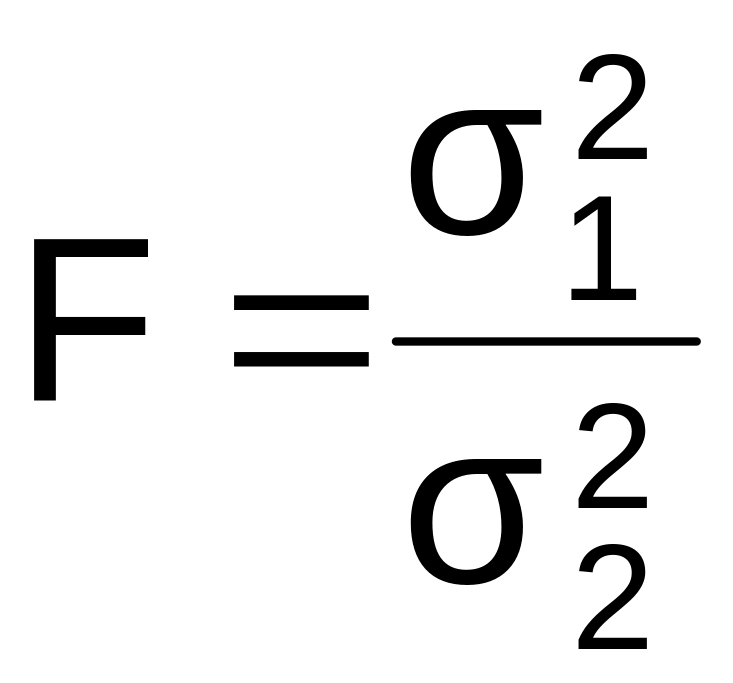