Лабораторна робота 2 Надійний інтервал. Перевірка статистичних гіпотез

Мета роботи:

навчитися застосовувати розрахунки надійного інтервалу випадкових величин з метою аналізу відповідності ознак друкованих та мультимедійних видань їхнім нормативам;

набути досвіду перевірки статистичних гіпотез стосовно рівня якості технологічних процесів у сфері поліграфії та мультимедіа.

Навчальний матеріал

1. Приклади законів розподілу деяких випадкових величин

Рівномірний розподіл. Рівномірний розподіл ймовірності є простим і може бути як дискретним, так і неперервним.

Дискретний рівномірний розподіл – це такий розподіл, для якого усі значення випадкової величини є рівноймовірними:

,

де k – кількість можливих значень випадкової величини.

Розподіл вірогідності неперервної випадкової величини Х, яка приймає значення з відрізку [а, b], називається рівномірним, якщо щільність розподілу випадкової величини на цьому відрізку є постійною, а поза ним дорівнює нулю (рис. 4-5):        

(8)

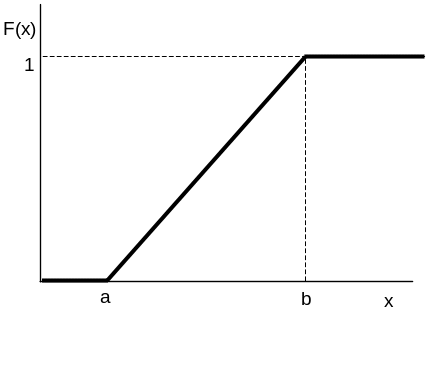
Рис. 4. Графік функції F(x) рівномірного розподілу

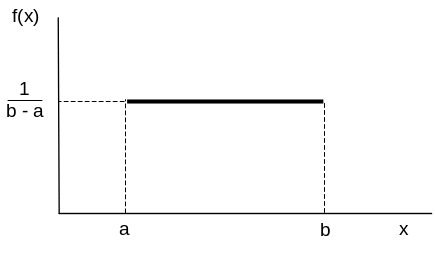
Рис. 5. Графік функції f(x) рівномірного розподілу

Для рівномірного розподілу випадкової величини Х математичне сподівання є серединою відрізку [а; b]:

,	(9)
.	(10)

Нормальний розподіл. Нормальним називається розподіл ймовірності неперервної випадкової величини, який описується щільністю ймовірності

,

(11)

де:

m ­– математичне сподівання випадкової величини,

­ – середньоквадратичне відхилення випадкової величини.

Нормальний закон розподілу займає центральне місце в теорії ймовірності і математичній статистиці. Це обумовлено тим, що нормальний закон проявляється у всіх випадках, коли випадкова величина є результатом дії великого числа різних чинників. Наприклад, помилки вимірювань розподілені за нормальним законом.

На практиці багато випадкових величин розподілені нормально або майже нормально: помилки стрільби; відхилення напруги в мережі від номіналу; сумарна ви­плата страхового товариства за довгостроковий період; дальність польоту снаряду; зріст чоловіків (жінок) одного віку і національності, й тому подібне (рис 6).

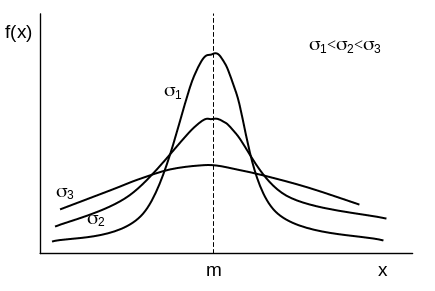
Рис. 6. Графік щільності розподілу випадкової величини, розподіленої за нормальним законом

Для випадкових величин, які розподілені за нормальним законом, діє правило трьох сигм.

Правило трьох сигм: якщо випадкова величина розподілена за нормальним законом, то ймовірність її відхилення від свого математичного сподівання на величину більше ніж 3 , (де ­ – середньоквадратичне відхилення випадкової величини), близька до нуля (точніше, дорівнює 0,0027). Іншими словами, практично достовірно, що нормальна випадкова вели­чина приймає значення з інтервалу [m-3 , m+3 ] (ймовірність цього дорівнює 0,9973).

2. Надійний інтервал випадкової величини

Надійний інтервал  випадкової величини з рівнем довіри (надійністю)  – це інтервал, який з ймовірністю  покриває всі вибіркові значення випадкової величини. Тобто всі вибіркові значення випадкової величини з ймовірністю  потрапляють в діапазон , де – вибіркове середнє (рис. 7).

Інтервал  для випадкової величини, яка має нормальний розподіл, визначається за формулою:

 =  · z,

(12)

де:

 – середнє квадратичне відхилення;

z – аргумент функції Лапласа, який визначається за допомогою відповідної таблиці для функції Лапласа Ф(z): вибирається таке z, для якого виконується умова: Ф(z) = /2, де  – надійна ймовірність.

Таблицю зі значеннями функції Лапласа подано у Додатку А.

Якщо не відоме середнє квадратичне відхилення σ, то у формулі розрахунку використовується виправлене вибіркове середнє квадратичне відхилення s та коефіцієнт Стьюдента t:

 = s · t,

(13)

де:

t – коефіцієнт Стьюдента, який вибирається з відповідної таблиці залежно від значення надійної ймовірності  і кількості ступенів свободи (кількість ступенів свободи дорівнює n –1).

Таблицю зі значеннями коефіцієнту t розподілу Стьюдента подано у Додатку Б.

Зауважимо, що при розрахунках надійного інтервалу для малої вибірки (при n<30) також використовується коефіцієнт Стьюдента t (а не аргумент функції Лапласа).

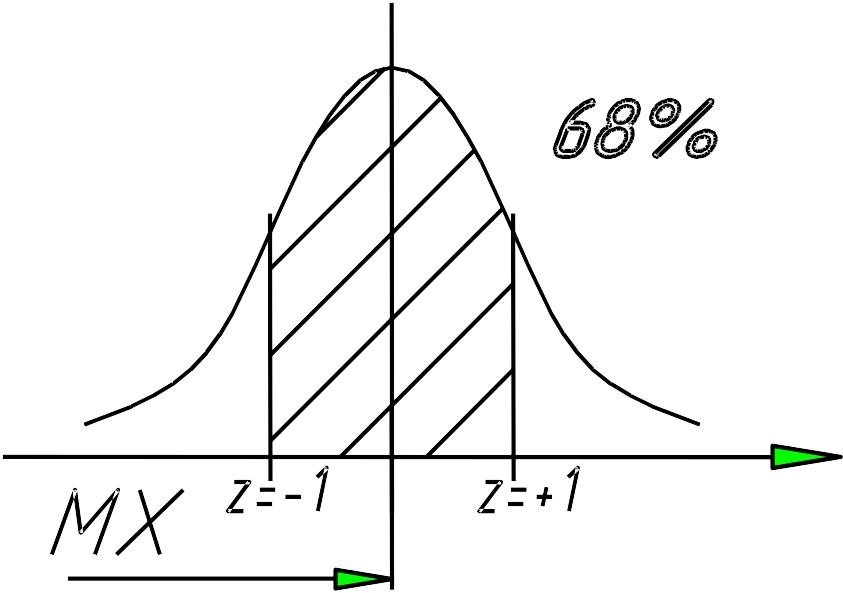
Рис. 7. Приклади надійних інтервалів із різними значеннями надійної ймовірності

Надійний інтервал _м математичного сподівання випадкової величини – це інтервал, який з великою ймовірністю містить значення математичного сподівання випадкової величини.

Надійна вірогідність _м – це ступінь упевненості в тому, що довірчий інтервал міститиме дійсне (невідоме) значення математичного сподівання генеральної сукупності.

Величина надійного інтервалу _м залежить як від надійної ймовірності _м, так і від об'єму вибірки n :

м= .

(14)

Приклад 1. Було здійснено вибірку 1600 осіб із сукупності усіх передплатників журналу «Видавничий бізнес». Середній вік за вибіркою – 30 років, середньоквадратичне відхилення – 10 років. Необхідно знайти надійний інтервал математичного сподівання.

Перш за все, необхідно задати надійну ймовірність оцінки. Візьмемо 95% надійність. Оскільки вибірка велика, скористаємося таблицею значень функції Лапласа (див. Додаток А) і знайдемо коефіцієнт довіри z=1,96. Тоді розрахуємо надійний інтервал  випадкової величини за формулою (11):

= 1,96*10=19,6.

Залишилося розрахувати надійний інтервал математичного сподівання формулою (13):

_м= =0,49.

З ймовірністю 95% істинний середній вік у генеральній сукупності знаходиться в інтервалі від 29,51 років до 30,49 років.
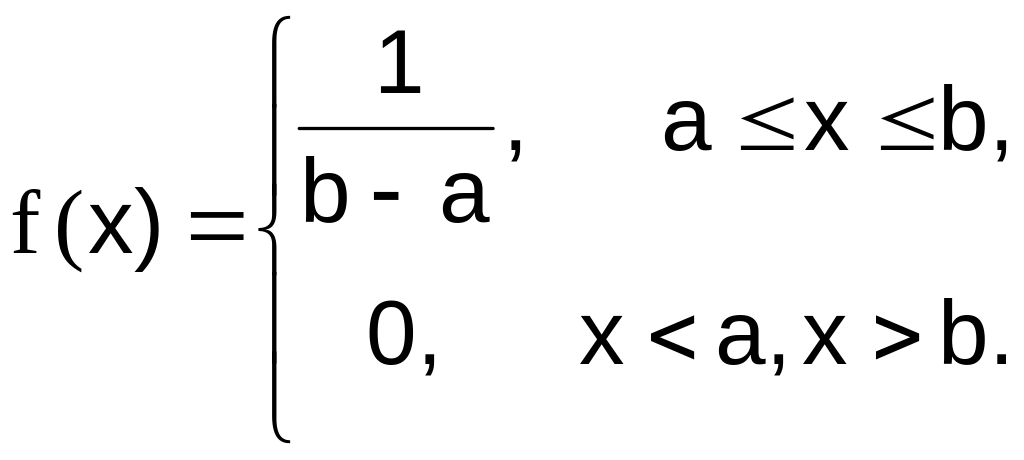
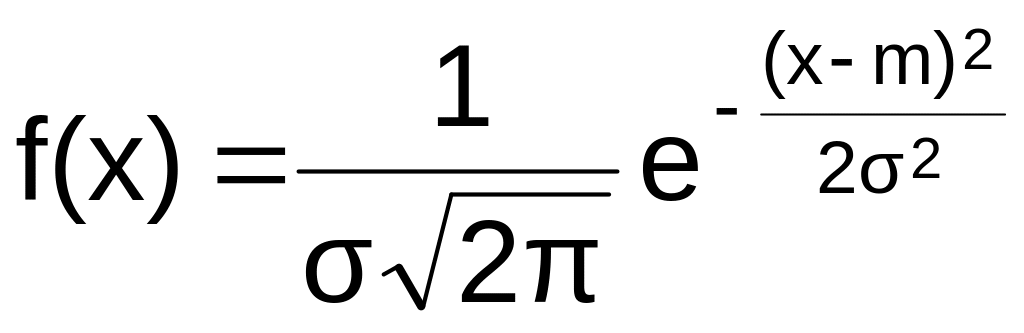