МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ
МЕТОДИЧНІ РЕКОМЕНДАЦІЇ
до виконання лабораторних робіт
з навчальної дисципліни
«Стандартизація і метрологія у поліграфії»
для студентів напряму підготовки
«Видавничо-поліграфічна справа»
усіх форм навчання
Укладач: Потрашкова Л.В.
Відповідальний за випуск Пушкар О.І.
Харків, ХНЕУ, 2010
Затверджено на засіданні кафедри комп’ютерних систем і технологій. Протокол № 7 від 24.03.2010 р.
Методичні рекомендації до виконання лабораторних робіт з навчальної дисципліни «Стандартизація і метрологія у поліграфії» для студентів напряму підготовки «Видавничо-поліграфічна справа» усіх форм навчання / Укл. Потрашкова Л. В. – Харків: Вид. ХНЕУ, 2010. - 49 с. (Укр. яз.)
Викладено методичні матеріали до виконання лабораторних робіт, призначених для формування умінь та навичок оцінки якості продукції у сфері поліграфії та мультимедіа.
Призначено для студентів напряму підготовки «Видавничо-поліграфічна справа».
Вступ
Ці рекомендації розроблені з метою надання методичної допомоги студентам в процесі виконання лабораторних робіт з курсу «Стандартизація і метрологія у поліграфії».
Мета розроблених лабораторних робіт полягає у формуванні в студентів таких умінь та компетенцій:
вміння застосовувати метод вибіркового спостереження в процесі дослідження якості друкованої та мультимедiйної продукції;
вміння визначати числові характеристики випадкових величин з метою аналізу розсіювання значень різних параметрів друкованих та мультимедійних видань;
вміння перевіряти статистичні гіпотези стосовно рівня якості та стабільності технологічних процесів у сфері поліграфії та мультимедіа;
вміння застосовувати методи кореляційного аналізу для відбору факторів, які суттєво впливають на якість поліграфічної та мультимедійної продукції;
вміння застосовувати методи кваліметрії для розрахунку показників якості друкованої та мультимедiйної продукції;
вміння застосовувати основні стандарти ергономіки мультимедіа-інтерфейсів для аналізу якості мультимедійних видань;
вміння реалізовувати вимоги ергономічних стандартів в процесі розробки мультимедiйної продукції.
Основною сферою реалізації вказаних вмінь та компетенцій є діяльність з оцінки, контролю та управління якістю поліграфічної та мультимедійної продукції.
Нагадаємо, що управління якістю є найважливішою передумовою успіху будь-якого підприємства (організації), у тому числі в галузі поліграфії та мультимедіа.
Також звертаємо увагу студентів, що вміння та навички, отримані в процесі виконання лабораторних робіт, будуть перевірені найближчим часом на екзамені з відповідної дисципліни «Стандартизація і метрологія у поліграфії».
Бажаємо успіху у навчанні!
Лабораторна робота 1 Числові характеристики статистичної вибірки
Мета роботи:
навчатися застосовувати вибірковий метод задля аналізу якості друкованих та мультимедійних видань
Навчальний матеріал
1. Математична статистика
Для контролю якості технологічних процесів створення друкованих та мультимедійних видань (насамперед, в поліграфії) використовуються методи математичної статистики. Вони є ефективним інструментарієм збору і аналізу інформації щодо якості виробничих операцій та готової продукції.
Математична статистика вивчає загальні питання аналізу масових кількісних даних та має справу з випадковими величинами (тобто з тими величинами, чиї значення визначаються множиною чинників випадкового характеру). Саме до таких – випадкових – величин відносяться характеристики технологічного процесу в поліграфії.
2. Поняття випадкової величини
Випадковою величиною називається така змінна величина, яка приймає те чи інше значення з деякої множини в залежності від випадку.
Виділяють дискретні та неперервні випадкові величини.
Дискретна випадкова величина – це випадкова величина, множина значень якої є скінченою або зліченною.
Неперервна випадкова величина приймає свої значення з множини дійсних чисел.
3. Закон розподілу дискретної випадкової величини
Будь-яка випадкова величина характеризується своїм розподілом, тобто описанням того, з якою частотою зустрічається кожне значення випадкової величини.
Для повного описання дискретної випадкової величини необхідно:
- вказати усі її можливі значення;
- задати ймовірність, з якою приймаються ці значення.
Відповідність між можливими значеннями дискретних випадкових величин та їхніми ймовірностями називається законом розподілу дискретної випадкової величини.
Зручно застосовувати табличний спосіб описання закону розподілу дискретної випадкової величини: у першому рядку таблиці вказують значення випадкової величини (хi, i=1, 2, 3…), в другому рядку – ймовірність цих значений (pi, i=1, 2, 3…). Таку таблицю називають рядом розподілу дискретної випадкової величини (табл. 1).
Таблиця 1
Ряд розподілу дискретної випадкової величини
Х |
х1 |
х2 |
… |
хi |
… |
P |
p1 |
p2 |
… |
pi |
… |
Оскільки дискретна випадкова величина обов'язково прийме одне зі своїх значень хi, події {хi, i=1, 2, 3…} утворюють повну групу подій, тобто виконується умова:
,
де pi, – ймовірність того, що випадкова величина прийме значення хi .
4. Функція та щільність розподілу випадкової величини
Ряд розподілу – не універсальна характеристика випадкової величини. Він існує тільки для дискретних випадкових величин.
Універсальною характеристикою, яка використовується як для дискретних, так і для неперервних випадкових величин, є функція розподілу.
Функція розподілу випадкової величини визначається формулою:
,
де: Х – значення випадкової величини,
х – дійсне число.
Функція розподілу випадкової величини X описує ймовірність того, що випадкова величина X набуде значень, менших заданого значення х, де х – будь-яке дійсне число.
Властивості F(x):
1. Значення F(x) належать відрізку [0, 1], тобто 0≤F(x)≤1.
2. F(x) – функція, що не убуває (тобто якщо x1<x2, то F(x1)≤F(x2)).
Похідна від функції розподілу F(x) називається щільністю розподілу випадкової величини: f(x)= F'((x) (рис. 1-3).
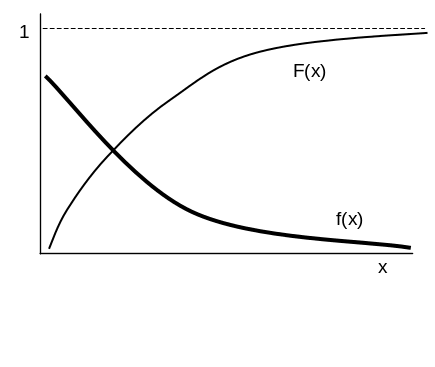
Рис. 1. Графіки функції розподілу та щільності розподілу випадкової величини, розподіленої за експоненціальним законом
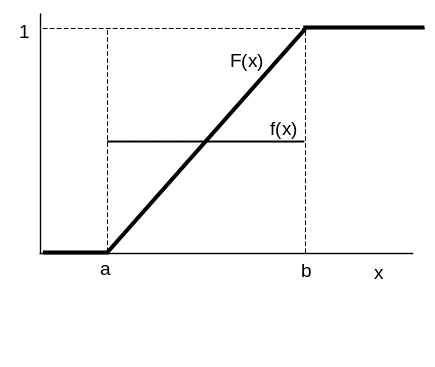
Рис. 2. Графіки функції розподілу та щільності розподілу випадкової величини, яка має рівномірний розподіл
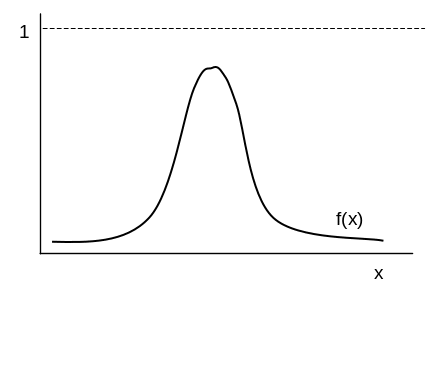
Рис. 3. Графік щільності розподілу випадкової величини, розподіленої за нормальним законом