4. Проектный и проверочный расчет закрытых зубчатых передач.
Первая ступень двухступенчатого редуктора – прямозубая цилиндрическая передача.
Определим
предварительное значение межосевого
расстояния
,
согласно /2, стр. 16/:
,
- передаточное
отношение,
- вращающий момент
на шестерне,
– коэффициент
поверхностной твердости зубьев шестерни
и колеса.
Знак плюс в скобках относится к внешнему зацеплению, знак минус к внутреннему зацеплению.
Коэффициент k
зависит от поверхностной твердости
зубьев шестерни и колеса, при
),
k
= 8, согласно /2, стр. 17/;
Вычисляем предварительное значение межосевого расстояния:
;
Окружную скорость v определяют по формуле, согласно /2, стр. 17/:
;
еделяем
степень точности зубчатой передачи, в
зависимости от окружной скорости,
согласно таблице 2,5, /2, стр. 17/:
Для прямозубой цилиндрической передачи, с окружной скоростью меньше 6 м/с, принимаем степень точности равную 8 –передача пониженной точности.
Уточним предварительно найденное значение межосевого расстояния по формуле, согласно /2, стр. 17/:
,
– коэффициент
профиля зубьев, для прямозубых колес,
,
- коэффициент
ширины, зависящий от положения колес
относительно опор, при несимметричном
расположении, согласно /2, стр. 17/:
,
выбирается из ряда стандартных чисел,
примем
.
- коэффициент
нагрузки.
Согласно /2, стр. 18/, коэффициент нагрузки определяется следующим образом:
,
где
- коэффициент, учитывающий внутреннюю
динамику нагружения,
- коэффициент,
учитывающий неравномерность распределения
нагрузки по длине контактных линий,
- коэффициент
распределения нагрузки между зубьями.
Коэффициент учитывает внутреннюю динамику нагружения, связанную, прежде всего с ошибками шагов зацепления и погрешностями профилей зубьев шестерни и колеса.
Значение
коэффициента
определяют по таблице 2.6 /2, стр.17/ в
зависимости от степени точности передачи
по нормам плавности, окружной скорости
и твердости рабочих поверхностей:
;
Коэффициент
учитывает неравномерность распределения
нагрузки по длине контактных линий,
обуславливаемую погрешностями
изготовления и упругими деформациями
валов, подшипников. Зубья зубчатых колес
могут прирабатываться: в результате
повышенного местного изнашивания
распределение нагрузки становится
более равномерным. Поэтому рассматривают
коэффициенты неравномерности распределения
нагрузки в начальный период работы
и после приработки
.
Значение коэффициента
принимают по таблице 2.7 /2, стр. 19/ в
зависимости от коэффициента
,
схемы передачи и твердости зубьев. Так
как ширина колеса и диаметр шестерни
еще не определены, значение коэффициента
вычисляется ориентировочно:
;
Согласно таблице 2.7 /2, стр.19/,
.
Коэффициент определяют по формуле:
,
где
- коэффициент, учитывающий приработку
зубьев, его значение зависит от окружной
скорости зубчатого колеса с меньшей
твердостью, согласно таблице 2.8 /2, стр.
19/:
;
Вычислим значение коэффициента :
;
Коэффициент определяют по формуле, согласно /2, стр. 18/:
,
где
– начальное значение коэффициента
распределения нагрузки между зубьями.
Согласно /2, стр. 20/, для прямозубых передач:
при условии 1 ≤
,
где
- степень точности передачи.
Вычислим начальное значение коэффициента распределения нагрузки между зубьями:
.
Вычислим значение коэффициента распределения нагрузки между зубьями:
.
Вычислим значение
коэффициента нагрузки
.
Уточним предварительно найденное значение межосевого расстояния:
(мм).
Определим предварительные основные размеры колеса, согласно /2, стр. 20/:
Делительный диаметр:
,115
(мм);
Ширина колеса:
(мм), окргуляем
полученное значение ширины колеса до
ближайшего большего стандартного
значения, по таблице 2.1 /2, стр. 410/:
;
Определим модуль передачи, согласно /2, стр.20/:
Максимально
допустимый модуль
,
мм определяют из условия неподрезания
зубьев у основания:
,
Минимально
допустимое значение модуля
,
мм определяют из условия прочности:
,
где
,
для прямозубых передач;
- допустимое
напряжение изгиба, равное минимальному
из
,
;
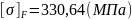- коэффициент
нагрузки, при расчете по напряжениям
изгиба.
Согласно /2, стр. 20/, коэффициент нагрузки по напряжениям изгиба , вычисляется следующим образом:
,
- коэффициент,
учитывающий внутреннюю динамику
нагружения,
– коэффициент,
учитывающий неравномерность распределения
напряжений у основания зубьев по ширине
зубчатого венца,
- коэффициент,
учитывающий влияние погрешностей
изготовления шестерни и колеса на
распределение нагрузки между зубьями.
Коэффициент
учитывает
внутреннюю динамику нагружения,
связанную, прежде всего с ошибками шагов
зацепления шестерни и колеса значение
коэффициента
определяется по таблице 2.9 /2, стр. 20/, в
зависимости от степени точности по
нормам плавности, окружной скорости и
твердости рабочих поверхностей:
.
Коэффициент оценивается по формуле, согласно /2, стр. 21/:
.
Коэффициент, учитывающий влияние погрешностей изготовления шестерни и колеса на распределение нагрузки между зубьями определяется так же, как при расчетах на контактную прочность:
.
Вычислим коэффициент нагрузки по напряжениям изгиба :
.
Вычисли минимально допустимое значение модуля :
(мм).
Из полученного диапозона допустимых значений модуля передачи принимаем меньшее значение модуля, согласуя его со стандартным, согласно /2, стр.21/:
.
Определим суммарное число зубьев, согласно /2, стр. 21/:
,
где
- угол наклона зубьев, для прямозубых
колес,
.
Вычислим значение суммарного числа зубьев:
,
полученное значение
округляют в меньшую сторону до целого
числа:
.
Определим число зубьев шестерни и колеса:
Согласно /2, стр. 21/ число зубьев шестерни определяется следующим образом:
Значение округляют в ближайшую сторону до целого числа:
.
Число зубьев колеса внешнего зацепления, согласно /2, стр. 22/:
.
Определим фактическое передаточное число, согласно /2, стр.22/:
.
Для двухступенчатых
редукторов, согласно /2, стр. 22/, ф
ское
значение передаточного числа не должно
отличаться от номинального более чем
на 4%:
.
Определим диаметры колес:
Делительные диаметры, согласно /2, стр. 22/:
Шестерни:
;
Колеса внешнего
зацепления:
;
Диаметры
и
вершин и впадин колес внешнего зацепления:
,
,
,
,
где
,
- коэффициенты смещения у шестерни и
колеса,
- коэффициент
воспринимаемого смещения, y
= - (
) / m,
a
– делительное межосевое расстояние,
.
Данные зубчатые колеса являются прямозубыми, коэффициенты смещения которых равны нулю, значит начальная и делительная окружности зацепления совпадают, а следовательно коэффициент воспринимаемого смещения, так же равен нулю.
;
y = - ( ) / m = 0.
Вычислим диаметры и вершин и впадин колес внешнего зацепления:
,
,
,
.
Определим размеры заготовок:
Чтобы получить при термической обработке принятые для расчета механические характеристики материала колес, требуется, что бы размеры заготовок колес не превышали предельно допустимых значений:
Согласно таблице 2.1 /2, стр. 11/ предельные размеры заготовок имеют значения:
,
Вычислим полученные размеры заготовок, согласно /2, стр. 22/:
Для цилиндрической
шестерни:
заготовок шестерни
соответствуют условию:
.
Для цилиндрического
колеса:
;
;
заготовок колеса соответствуют условиям:
,
.
Проверка зубьев колес по контактным напряжениям:
Расчетное значение контактного напряжения, согласно /2, стр. 23/:
,
где
для прямозубых передач;
Вычислим расчетное значение контактного напряжения:
.
Согласно /2, стр.23/,
если расчетное напряжение
меньше допускаемого
в пределах 15..20% или
больше
в пределах 5%, то ранее принятые параметры
передачи принимают за окончательные.
.
ранее принятые
параметры передачи за окончательные.
Определим силы в зацеплении передачи:
Данная зубчатая передача является цилиндрической прямозубой, поэтому в зацеплении действуют две силы это окружная и радиальная:
Вычислим значение окружной силы, согласно /2, стр.23/:
;
значение
радиальной силы, /2, стр.23/:
,
стандартном
значении угла
.
Проверка зубьев колес по напряжениям изгиба:
Расчетное напряжение изгиба в зубьях колеса, согласно /2, стр. 23/:
,
Расчетное напряжение изгиба в зубьях шестерни:
,
значение коэффициента
, учитывающего форму зуба и концентрацию
напряжений, в зависимости от приведенного
числа зубьев
и коэффициента смещения для внешнего
зацепления принимают по таблице 2.10 /2,
стр. 24/:
;
;
Коэффициент
учитывает угол наклона зубьев в косозубой
передаче, для прямозубой передачи
Коэффициент
учитывает перекрытие зуба, в прямозубой
передаче с 8 степенью точности
.
Вычисляем расчетное напряжение изгиба в зубьях шестерни и колеса:
для колеса:
,
для шестерни:
.
(МПа),
,
,
,
зубья шестерни и колеса проходят проверку по напряжениям изгиба.
Вторая ступень двухступенчатого редуктора – прямозубая цилиндрическая передача.
Определим предварительное значение межосевого расстояния , согласно /2, стр. 16/:
,
- передаточное отношение,
- вращающий момент
на шестерне,
– коэффициент поверхностной твердости зубьев шестерни и колеса.
Знак плюс в скобках относится к внешнему зацеплению, знак минус к внутреннему зацеплению.
Коэффициент k зависит от поверхностной твердости зубьев шестерни и колеса, при ), k = 8, согласно /2, стр. 17/;
Вычисляем предварительное значение межосевого расстояния:
;
Окружную скорость v определяют по формуле, согласно /2, стр. 17/:
;
еделяем степень точности зубчатой передачи, в зависимости от окружной скорости, согласно таблице 2,5, /2, стр. 17/:
Для прямозубой цилиндрической передачи, с окружной скоростью меньше 6 м/с, принимаем степень точности равную 9 –передача низкой точности.
Уточним предварительно найденное значение межосевого расстояния по формуле, согласно /2, стр. 17/:
,
– коэффициент профиля зубьев, для прямозубых колес, ,
- коэффициент
ширины, зависящий от положения колес
относительно опор, при несимметричном
расположении, согласно /2, стр. 17/:
,
выбирается из ряда стандартных чисел,
примем
.
- коэффициент нагрузки,
.
Согласно /2, стр. 18/, коэффициент нагрузки определяется следующим образом:
,
где - коэффициент, учитывающий внутреннюю динамику нагружения,
- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий,
- коэффициент распределения нагрузки между зубьями.
Коэффициент учитывает внутреннюю динамику нагружения, связанную, прежде всего с ошибками шагов зацепления и погрешностями профилей зубьев шестерни и колеса.
Значение
коэффициента
определяют по таблице 2.6 /2, стр.17/ в
зависимости от степени точности передачи
по нормам плавности, окружной скорости
и твердости рабочих поверхностей:
;
Коэффициент учитывает неравномерность распределения нагрузки по длине контактных линий, обуславливаемую погрешностями изготовления и упругими деформациями валов, подшипников. Зубья зубчатых колес могут прирабатываться: в результате повышенного местного изнашивания распределение нагрузки становится более равномерным. Поэтому рассматривают коэффициенты неравномерности распределения нагрузки в начальный период работы и после приработки .
Значение коэффициента принимают по таблице 2.7 /2, стр. 19/ в зависимости от коэффициента , схемы передачи и твердости зубьев. Так как ширина колеса и диаметр шестерни еще не определены, значение коэффициента вычисляется ориентировочно:
;
Согласно таблице 2.7 /2, стр.19/,
.
Коэффициент определяют по формуле:
,
где - коэффициент, учитывающий приработку зубьев, его значение зависит от окружной скорости зубчатого колеса с меньшей твердостью, согласно таблице 2.8 /2, стр. 19/:
;
Вычислим значение коэффициента :
;
Коэффициент определяют по формуле, согласно /2, стр. 18/:
,
где – начальное значение коэффициента распределения нагрузки между зубьями.
Согласно /2, стр. 20/, для прямозубых передач:
при условии 1 ≤
,
где - степень точности передачи.
Вычислим начальное значение коэффициента распределения нагрузки между зубьями:
.
Вычислим значение коэффициента распределения нагрузки между зубьями:
.
Вычислим значение коэффициента нагрузки
.
Уточним предварительно найденное значение межосевого расстояния:
(мм).
Определим предварительные основные размеры колеса, согласно /2, стр. 20/:
Делительный диаметр:
(мм);
Ширина колеса:
(мм), округляем
полученное значение ширины колеса до
ближайшего большего стандартного
значения, по таблице 24.1 /2, стр. 410/:
;
Определим модуль передачи, согласно /2, стр.20/:
Максимально допустимый модуль , мм определяют из условия неподрезания зубьев у основания:
,
Минимально допустимое значение модуля , мм определяют из условия прочности:
,
где , для прямозубых передач;
- допустимое напряжение изгиба, равное минимальному из , ;
- коэффициент нагрузки, при расчете по напряжениям изгиба.
Согласно /2, стр. 20/, коэффициент нагрузки по напряжениям изгиба , вычисляется следующим образом:
,
- коэффициент, учитывающий внутреннюю динамику нагружения,
– коэффициент, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца,
- коэффициент, учитывающий влияние погрешностей изготовления шестерни и колеса на распределение нагрузки между зубьями.
Коэффициент учитывает внутреннюю динамику нагружения, связанную, прежде всего с ошибками шагов зацепления шестерни и колеса значение коэффициента определяется по таблице 2.9 /2, стр. 20/, в зависимости от степени точности по нормам плавности, окружной скорости и твердости рабочих поверхностей:
.
Коэффициент оценивается по формуле, согласно /2, стр. 21/:
.
Коэффициент, учитывающий влияние погрешностей изготовления шестерни и колеса на распределение нагрузки между зубьями определяется так же, как при расчетах на контактную прочность:
.
Вычислим коэффициент нагрузки по напряжениям изгиба :
.
Вычисли минимально допустимое значение модуля :
(мм).
Из полученного диапозона допустимых значений модуля передачи принимаем меньшее значение модуля, согласуя его со стандартным, согласно /2, стр.21/:
.
Определим суммарное число зубьев, согласно /2, стр. 21/:
,
где - угол наклона зубьев, для прямозубых колес, .
Вычислим значение суммарного числа зубьев:
,
полученное значение округляют в меньшую сторону до целого числа:
.
Определим число зубьев шестерни и колеса:
Согласно /2, стр. 21/ число зубьев шестерни определяется следующим образом:
Значение округляют в ближайшую сторону до целого числа:
.
Число зубьев колеса внешнего зацепления, согласно /2, стр. 22/:
.
Определим фактическое передаточное число, согласно /2, стр.22/:
.
Для двухступенчатых редукторов, согласно /2, стр. 22/, ф ское значение передаточного числа не должно отличаться от номинального более чем на 4%:
.
Определим диаметры колес:
Делительные диаметры, согласно /2, стр. 22/:
Шестерни:
;
Колеса внешнего
зацепления:
;
Диаметры и вершин и впадин колес внешнего зацепления:
,
,
,
,
где , - коэффициенты смещения у шестерни и колеса,
- коэффициент воспринимаемого смещения, y = - ( ) / m,
a – делительное межосевое расстояние, .
Данные зубчатые колеса являются прямозубыми, коэффициенты смещения которых равны нулю, значит начальная и делительная окружности зацепления совпадают, а следовательно коэффициент воспринимаемого смещения, так же равен нулю.
;
y = - ( ) / m = 0.
Вычислим диаметры и вершин и впадин колес внешнего зацепления:
,
,
,
.
Определим размеры заготовок:
Чтобы получить при термической обработке принятые для расчета механические характеристики материала колес, требуется, что бы размеры заготовок колес не превышали предельно допустимых значений:
Согласно таблице 2.1 /2, стр. 11/ предельные размеры заготовок имеют значения:
,
Вычислим полученные размеры заготовок, согласно /2, стр. 22/:
Для цилиндрической
шестерни:
заготовок шестерни соответствуют условию:
.
Для цилиндрического
колеса:
;
;
заготовок колеса не соответствуют условию:
.
Изменим способ термической обработки колеса цилиндрической передачи:
принимаем
вид ТО – улучшение с твердостью
поверхности зубьев
);
Тогда
предельные размеры заготовки колеса
.
Определим допускаемые контактные и изгибные напряжения для колеса второй ступени двухступенчатого редуктора:
Допускаемые контактные напряжения:
,
Значения
коэффициентов
и
остаются неизменными:
;
;
;
;
Вычислим предел контактной выносливости:
;
Вычислим допускаемые контактные напряжения:
;
Допускаемые напряжения изгиба:
,
Значения
коэффициентов
остаются неизменными:
,
,
,
.
Вычислим предел выносливости при отнулевом цикле нагружения:
;
Вычислим значение допускаемых напряжений изгиба:
.
Для дальнейших расчетов принимаем минимальные из допускаемых контактных напряжений и напряжений изгиба, то есть:
,
.
Проверка зубьев колес по контактным напряжениям:
Расчетное значение контактного напряжения, согласно /2, стр. 23/:
,
где для прямозубых передач;
Вычислим расчетное значение контактного напряжения:
.
Согласно /2, стр.23/, если расчетное напряжение меньше допускаемого в пределах 15..20% или больше в пределах 5%, то ранее принятые параметры передачи принимают за окончательные.
.
ранее принятые параметры передачи за окончательные.
Определим силы в зацеплении передачи:
Данная зубчатая
передача является цилиндрической
прямозубой, поэтому в зацеплении
действуют две силы это окружная и
радиальная:
Вычислим значение окружной силы, согласно /2, стр.23/:
;
значение радиальной силы, /2, стр.23/:
,
стандартном значении угла .
Проверка зубьев колес по напряжениям изгиба:
Расчетное напряжение изгиба в зубьях колеса, согласно /2, стр. 23/:
,
Расчетное напряжение изгиба в зубьях шестерни:
,
значение коэффициента , учитывающего форму зуба и концентрацию напряжений, в зависимости от приведенного числа зубьев и коэффициента смещения для внешнего зацепления принимают по таблице 2.10 /2, стр. 24/:
;
;
Коэффициент учитывает угол наклона зубьев в косозубой передаче, для прямозубой передачи
Коэффициент учитывает перекрытие зуба, в прямозубой передаче с 9 степенью точности .
Вычисляем расчетное напряжение изгиба в зубьях шестерни и колеса:
для колеса:
,
для шестерни:
.
(МПа), ,
,
,
зубья шестерни и колеса проходят проверку по напряжениям изгиба.