Порядок виконання роботи.

1. Визначити фондоозброєність постійну в часі, що є рішенням моделі (1). Вихідні дані наведені в табл.1.

2. Вирішити різницеве рівняння (1) за допомогою Va000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 для k₀ = 0,1*N, де N-Номер студента по журналі, t змінюється від 1 до 30, виразивши k_t+1 з (1). Побудувати графік функції.

3. Побудувати таблицю, що відображає зміну показників Y, K, L і C, і відобразити графічно.

4. Визначити оптимальне значення норми нагромадження 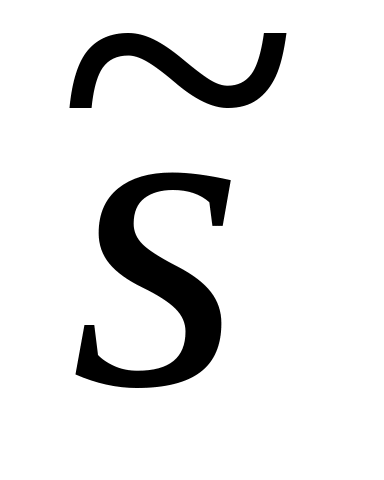, що забезпечує максимальне споживання на 1 працюючого.

5. Побудувати графік для величин Y, K, L і C, що відповідають оптимальній нормі нагромадження , і зрівняти із цими ж величинами, отриманими для s, заданого в табл. 1.

Таблиця1

ВВаріант	g- приріст робочої сили	(-коефіцієнт вибуття основних фондів	s-норма нагромадження	Параметр виробничої функції Кобба-Дугласа,
1	0,01	0,8	0,4	A=16 =0,2
2	0,04	0,7	0,9	A=20 =0,9
3	0,13	0,2	0,1	A=8 =0,6
4	0,2	0,3	0,2	A=12 =0,4
5	0,05	0,8	0,8	A=18 =0,5
6	0,09	0,9	0,6	A=14 =0,2
7	0,12	0,5	0,5	A=10 =0,7
8	0,08	0,1	0,3	A=16 =0,3
9	0,03	0,8	0,2	A=16 =0,9
10	0,15	0,4	0,7	A=20 =0,6
				Продовження таблиці1
11	0,19	0,6	0,6	A=12 =0,2
12	0,1	0,5	0,1	A=8 =0,5
13	0,02	0,1	0,3	A=18 =0,2
14	0,08	0,2	0,8	A=6 =0,8
15	0,21	0,7	0,9	A=20 =0,5
16	0,03	0,5	0,4	A=14 =0,4
17	0,05	0,3	0,5	A=16 =0,3
18	0,2	0,6	0,7	A=12 =0,7
19	0,15	0,6	0,2	A=12 =0,8
20	0,03	0,2	0,3	A=20 =0,9
21	0,06	0,5	0,8	A=10 =0,5
22	0,01	0,1	0,4	A=16 =0,3

Література

1. Гранберг А.Г. Динамические модели народного хозяйства. М.: Экономика, 1985

2. Гранберг А.Г. Моделирование социальной экономики. М.: Экономика, 1998

3. Экономическая кибернетика, под ред. Лысенко. Изд-во Донецкого государственного университета.

4. Иванилов Ю.П., Лотов А.В. Математические модели в экономике.

5. Математическая экономика на персональном компьютере. Под ред. М.Кубониса.