4.2 Характеристики стаціонарної траєкторії.

Стаціонарна траєкторія – зміна макроекономічних характеристик у часі при постійної фондоозброєності.

Під характеристиками розуміється: обсяг основних фондів K_t, обсяг трудових ресурсів L_t, обсяг кінцевого продукту Y_t. Зміна цих характеристик у часі, що задається відповідно дискретними функціями описує стаціонарну траєкторію. Ця траєкторія відповідає постійної фондоозброєності , t=0, 1, 2...

Величина - рішення різницевого рівняння дискретної моделі Солоу, перебуває з рішення рівняння (4.8). З визначення фондоозброєності й з обліком того, що вона є постійною в часі величиною, треба

,

де k₀ – фондоозброєність праці в початковий момент часу; L₀ – обсяг трудових ресурсів у початковий момент часу; K₀ – обсяг основних фондів у початковий момент часу.

З рівняння (4.7) випливають наступні вираження для функцій .

Обсяг трудових ресурсів:

, t=0,1,2, (4.9)

де L₀ – обсяг трудових ресурсів у початковий момент часу;

Обсяг основних фондів:

, (4.10)

де K₀ – обсяг основних фондів у початковий момент часу.

Обсяг кінцевого продукту:

, (4.11)

де Y₀ – обсяг кінцевого продукту в початковий момент часу.

Всі зазначені характеристики ростуть із постійним темпом росту (1+g). При цьому постійні:

середня продуктивність праці ,

середня фондовіддача .

фонд споживання на 1 зайнятого .

Дана траєкторія є стійкої, що затверджується в наступній теоремі.

Теорема 4.2. При будь-якій величині фондоозброєності в початковий момент часу t=0, , рішення рівняння (4.7) при . Збіжність монотонна, див. мал. 4.2

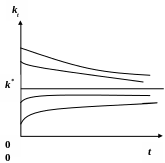
Рис. 4.2

4.3 Оптимізація процесу розвитку економічної системи.

Оптимальна постійна норма нагромадження

Величина - постійної фондоозброєності залежить від параметрів , що ілюструє малюнок 4.3.

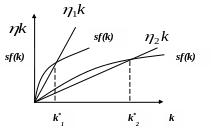
Рис. 4.3

Нехай варіюється один параметр – норма нагромадження s. Знайдемо оптимальну величину s. Як критерій оптимальності виберемо споживання на один працюючого с. Із цією метою вирішимо завдання

. (4.12)

Необхідна умова максимуму для завдання (4.12):

, (4.13)

З формул (4.12) і (4.13) одержуємо:

.

У зв'язку з тим, що фондоозброєність залежить від норми нагромадження, . Тому

, (4.14)

Значення , що задовольняє рівнянню (4.14), перебуває із цього рівняння при підстановці в нього конкретного значення виробничої функції . Згідно (4.8) і (4.14) оптимальне значення s, що відповідає оптимальної фондоозброєності , визначається в такий спосіб

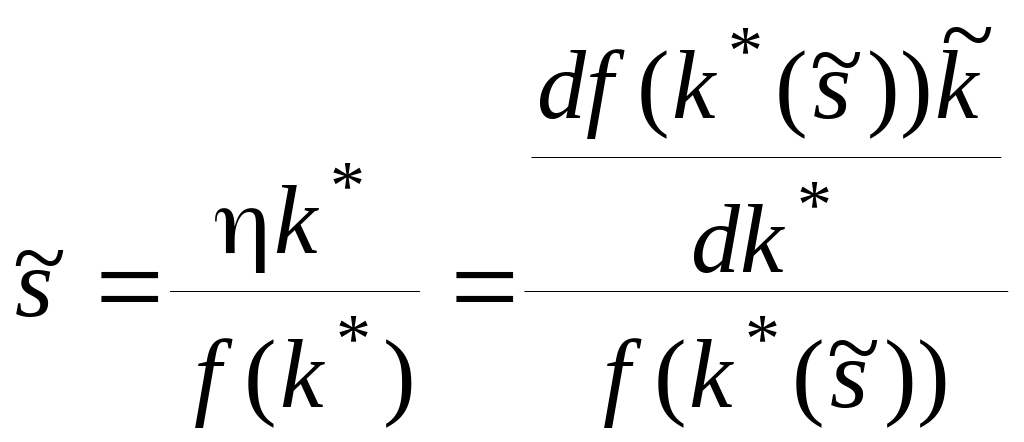, (4.15)

де .

Розглянемо економічний зміст . Із цією метою введемо поняття еластичності функції.

Еластичністю функції n змінних , де вектор 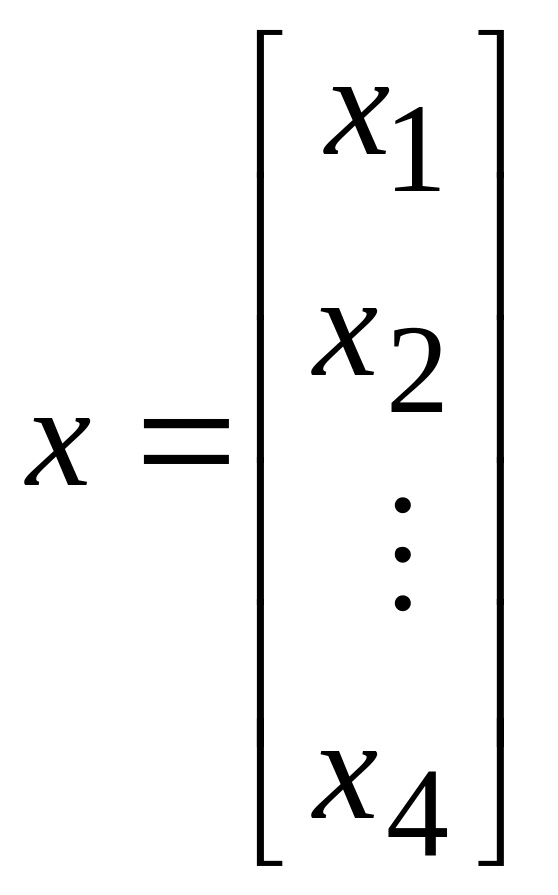, по змінній називається величина

. (4.16)

Визначимо еластичність виробничої функції, що задає обсяг кінцевого продукту , див. (4.1), по розмірі капітальних вкладень K. Згідно (4.16) ця величина

.

У зв'язку з тим, що в справжніх методичних вказівках розглядаються виробничі функції лінійно однорідні при всіх K, L згідно (4.6) маємо . Звідси

, .

З останніх двох виражень і (4.15) одержуємо

,

де такі, що .

Для виробничої функції Кобба-Дугласа або . Звідси згідно (4.15)

.

Отже, для цієї функції : еластичність виробничої функції по основних фондах дорівнює оптимальній нормі нагромадження.

Описаний похід до оптимізації норми споживання запропонований Э. Фелпсом і відомий як «золоте правило» економічного росту.

На мал.4.4 графічно показаний зміст визначення оптимальної норми нагромадження.

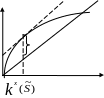
Рис.4.4