Зміст

I Методичні вказівки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ...4

Введення...…………………………………………………………......4

1. Показники економічної динаміки...…………………………......5

2. Поняття динамічної рівноваги в економіці. Найпростіша модель рівноваги...……………………………………………………………......6

3. Проста модель макроекономічної динаміки...………………………………………………………………………...... 9

4. Однофакторна модель економічної динаміки (дискретний аналог моделі Солоу)...……………………………………………………….......10

   1. Висновок моделі...…………………………………………......0

   2. Характеристики стаціонарної траєкторії...…………......2

   3. Оптимізація процесу розвитку економічної системи. Оптимальна постійна норма виробничого нагромадження....14

   4. Визначення оптимальної норми нагромадження ……...15

   5. Модель Шелла...……………………………………….......16

II Індивідуальні завдання...……………………………………………18

Порядок виконання індивідуальних робіт...……………………......18

Завдання 1...……………………………………………………… ......9

Завдання 2...……………………………………………………… ......1

Завдання 3...……………………………………………………....... . 24

Додаток А. Зразок оформлення титульного аркуша...……………...... 26

Список використаної літератури...…………………………………….......27

I Методичні вказівки

Введення

Економічні завдання діляться залежно від обліку часу на статичні й динамічні. Статика вивчає стан економічних систем у певний момент часу або період часу. Динаміка вивчає залежність змінних і параметрів економічних систем у часі. Наприклад, динаміка інвестицій визначає динаміку величин основного капіталу, що у свою чергу є найважливішим чинником зміни обсягу випуску в часі.

Час в економічній динаміці може розглядатися як безперервне й дискретне. Яке ж подання часу в економічних моделях треба вибирати? Реально економічні змінні - безперервні. Відлік - дискретний. Тому економічні змінні - дискретні функції часу.

Однак, подання економічних змінних як безперервних функцій, становить інтерес при побудові безперервних економічних динамічних моделей. При цьому застосовується математичний апарат диференціальних рівнянь. Цей апарат добре розроблений у класичній математиці. Для опису динамічних дискретних моделей використовується апарат різницевих рівнянь.

Більшість економічних динамічних моделей існують як у безперервному, так і дискретному варіантах. В обох варіантах для них може бути отримані, як правило, аналогічні результати. Це пояснюється тим, що рішення звичайних диференціальних і різницевих рівнянь подібні й мають схожу конструкцію.

Далі будуть використовуватися наступні позначення: безперервні змінні – x(t), дискретні - x_t..

У даному керівництві, в основному, будуть використовуватися дискретні моделі, тому що ряди динаміки економічних показників являють собою дискретні тимчасові ряди.

1.Показники економічної динаміки.

1. Абсолютний приріст ,

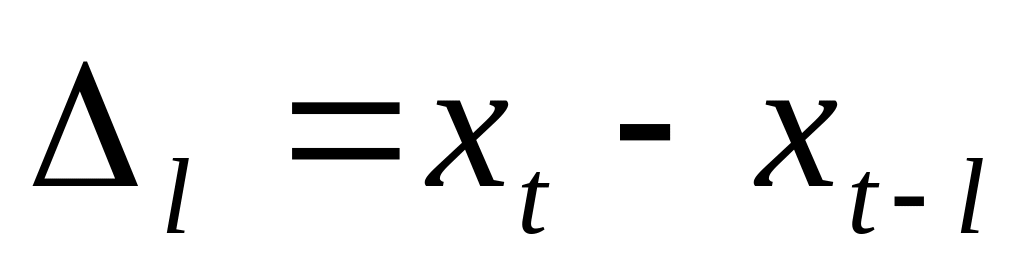де x_t. і x_t-1 - значення економічного показника відповідно в момент часу t і t-l .

2. Темп росту (коефіцієнт росту) , є відносною величиною. У статистику він називається ланцюговим коефіцієнтом росту.

3. Темп приросту 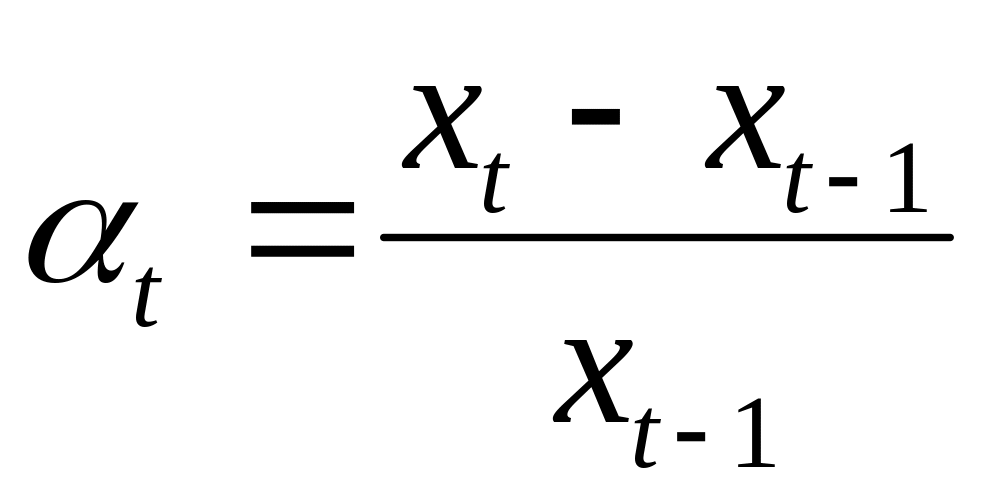також є відносною величиною. Між темпом росту й темпом приросту існує залежність:

_, (1.1)

Якщо темп приросту постійний у часі: то

.

2.Поняття динамічної рівноваги в економіці. Найпростіша модель рівноваги

Розглянемо моделі рівноваги для дискретного й безперервного часу.

1) Час - безперервна величина.

Будемо вважати, що швидкість зміни показника x(t) пропорційна величині його відхилення від рівноважного значення x_e,, індекс е – перша буква слова equilibrimm (рівновага). Відповідно до даного припущення, чим далі перебуває показник від стану рівноваги, тим швидше він прагне до нього повернутися. Таким чином,

_{, (2.1)}

де k - коефіцієнт

Перетворимо рівняння (2.1):

_(2.2)

Рішення (2.2) має такий вигляд:

_,

де - рішення однорідного рівняння , -частка рішення (2.2).

З метою одержання вираження для _{представимо} диференціальне рівняння (2.2) в операторному виді

_,

_{де - оператор диференціювання.}

_{З отриманого вираження одержуємо характеристичне рівняння, що відповідає диференціальному рівнянню (2.2):}

^._.

_{Його рішення p=k. Воно використовується у вираженні для загального рішення однорідного диференціального рівняння:}

_.

де С – деяка константа. Вона визначається по початковій умові х(0): значенню при t=0.

Нехай х(0) відомо. Маємо з (2.1) з урахуванням вираження для _:

_{З даного вираження для t=0 маємо}

_.

_{Звідси треба}

_.

Таким чином, .

Приватне рішення рівняння (2.2) : Воно обертає (2.2) у тотожність. Підставивши знайдені вираження для _й у формулу для , одержимо остаточне вираження для рішення диференціального рівняння (2.2)

.

2) Час - дискретна величина

Дискретна модель аналогічна диференціальному рівнянню (2.1):

_{де - значення показника в дискретний момент часу t. Після приведення подібних членів одержуємо:}

_, (2.3)

Рішення (2.3):

.

Тут ,

де q-рішення характеристичного рівняння ^,

Таким чином, , звідки (збігається з величиною Із для диференціального рівняння).

Тоді _.