- •Розділ 1. Основи двійкової арифметики
- •Тема 1.1. Подання чисел з фіксованою комою в розрядній сітці Подання чисел в еом
- •Завдання для самоконтролю
- •Завдання для самоконтролю
- •Представлення чисел з фіксованою комою
- •Завдання для самоконтролю
- •Кодування знаків і від’ємних чисел
- •Тема для самостійного опрацювання (Лекція №1с): Виконання операцій додавання та віднімання чисел з фк
- •Алгоритми множення в еом
- •Виконання операцій зсуву
- •Завдання для самоконтролю
- •Перший основний алгоритм множення
- •Другий основний алгоритм множення
- •Третій основний алгоритм множення
- •Четвертий основний алгоритм
- •Завдання для самоконтролю
- •Тема для самостійного опрацювання (Лекція №2с): Алгоритми ділення в еом
- •Тема 1.2. Виконання арифметичних операцій над числами з плаваючою комою (пк) Подання чисел з плаваючою (блукаючою) комою
- •Завдання для самоконтролю
- •Виконання операцій додавання та віднімання чисел з плаваючою комою
- •Завдання для самоконтролю
- •Тема для самостійного опрацювання (Лекція №3с): Множення, ділення чисел з пк
- •Тема 2.1 Основні функції та теореми алгебри логіки
- •Основні поняття і закони алгебри логіки
- •Булеві теореми та закони
- •Завдання для самоконтролю
- •Тема для самостійного опрацювання (Лекція №4с): Цифровий сигнал та способи його передачі
- •Функціонально повні системи логічних елементів
- •Структурна схема таких пристроїв має вигляд
- •Часова діаграма тактового сигналу
- •Базові логічні елементи
- •Завдання для самоконтролю
- •Тема для самостійного опрацювання (Лекція №5с): Допоміжні логічні функції
- •Завдання для самоконтролю
- •Тема 2.2. Мінімізація логічних функцій Форми представлення логічних функцій
- •Завдання для самоконтролю
- •Мінімізація логічних функцій
- •Тема для самостійного опрацювання (Лекція №6с): Мінімізація логічних функцій аналітичним способом
- •Мінімізація логічних функцій методом Карно – Вейча
- •Закріплення матеріалу лекції
- •Підготовка до виконання лабораторної роботи №4
- •Розділ 3. Схемотехніка комбінаційних схем
- •Тема 3.1 Дешифратори (dc), шифратори (cd), мультиплексори (ms), демультиплексори-селектори (dm) Дешифратор (Decoder)
- •Тема для самостійного опрацювання (Лекції №8,9с): Лінійні та каскадні дешифратори Дешифратори на сіс
- •Шифратор (Coder)
- •Мультиплексор
- •Демультиплексор
- •Тема для самостійного опрацювання (Лекція №10с): Комбінаційні пристрої на імс
- •Підготовка до виконання лабораторної роботи №5
- •Завдання для самоконтролю
- •Тема 3.2. Перетворювачі кодів Перетворювачі кодів, робота, призначення
- •Тема для самостійного опрацювання (Лекція №11с): Перетворювач двійкового коду в семи сегментний для цифрової індикації
- •Перетворювач прямого коду в додатковий
- •Завдання для самоконтролю
- •Підготовка до виконання лабораторної роботи №6
Функціонально повні системи логічних елементів
Цифрові схеми проектуються для того, щоб генерувати вихідну напругу, яка потрапляє в діапазони, які визначені для „0” і „1”, це означає, що цифрова схема реагує однаково на усі вхідні напруги, які потрапляють в діапазон „0” або „1” значень, а не на фактичні значення напруги.
Цей принцип можна представити так:

Цифрова схема є повністю цифровою якщо вхідні та вихідні сигнали відображаються «лог 1» або «лог 0», тобто одним з двох можливих рівнів напруги. В залежності від розв’язування задачі будь-якому заданому набору вхідних сигналів повинен відповідати цілком визначений набір вихідних сигналів. Залежність між вхідними і вихідними сигналами може бути визначатися також і станом цифрового пристрою, в якому він знаходився в попередній момент часу.
Таким чином задачу проектування корисно розчленувати на дві частини: проектування комбінаційних цифрових схем (КЦП або КЛС) і послідовнісних (ПЦП).
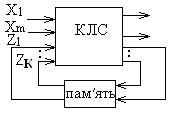
Комбінаційні логічні схеми (КЛС, КЦП) – не містить елементів пам’яті і тому значення її вихідних сигналів повністю визначаються теперішніми (поточними) значеннями її вхідних сигналів тому аналіз і проектування КЛС значно простіше.
Структурна схема таких пристроїв має вигляд
|
|
П |
Послідовністні логічні схеми (ПЛС або ПЦП) це схеми з пам’яттю (запам’ятовуючим пристроєм). Значення вихідного сигналу f1…fn, цього пристрою залежить від визначених кодів (значень) вхідних сигналів х1…хm y поточний момент часу і від стану елементів пам’яті z1…zk, в якому вони були на попередніх тактах.
|
|
↑ (синхронізація) – може бути |
|
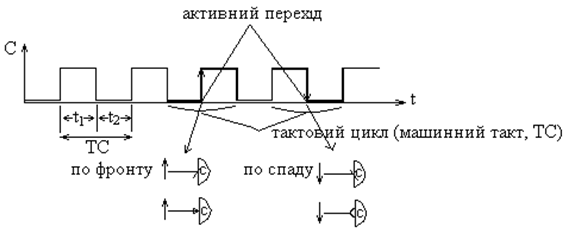
В усіх комп’ютерах використовують генератор тактових імпульсів (ГТІ), що виробляє періодичну послідовність прямокутних імпульсів, які називаються тактовими (С). На початок кожного імпульсу С відбувається зміна інформації на входах елементів і вузлів цифрових пристроїв. Принцип подачі інформації на входи елементів і вузлів у тактові моменти називається дискретизацією сигналів у часі.
Тактовий сигнал – це є серія імпульсів фіксованої ширини зі фіксованою частотою повторення. Тактові імпульси називають синхронізуючими або синхроімпульсами (t1 = t2).
Часова діаграма тактового сигналу
І комбінаційні пристрої і пристрої з пам’яттю реалізуються на основі логічних (булевих) функцій.
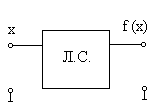
Булеву функцію
 можна задати трьома способами:
можна задати трьома способами:
змістовно ( словесний опис);
таблично (таблиця істинності);
алгебраїчно.
Алгебраїчний спосіб задання булевої функції представляє собою формулу зв'язану простішими логічними операціями І, АБО, НЕ, І-НЕ, АБО-НЕ (табл. 1).
Таблиця 1. Елементарні логічні функції.
Логічна операція (назва функції) |
Задання функції формулою |
Таблиця істинності |
||
входи |
виходи |
|||
Х2 |
Х1 |
f(х1,х2) |
||
І (кон’юнкція, логічне множення) |
f(х1,х2)= х1х2 f(х1,х2)= х1х2 f(х1,х2...хn)= х1х2... хn |
0 0 1 1 |
0 1 0 1 |
0 0 0 1 |
АБО (диз’юнкція, логічне додавання) |
f(х1,х2)= х1+х2 f(х1,х2)= х1х2 f(х1,х2...хn)= х1х2...хn |
0 0 1 1 |
0 1 0 1 |
0 1 1 1 |
НЕ (інверсія, заперечення) |
|
|
0 1 |
1 0 |
І-НЕ (функція Шеффера) |
|
0 0 1 1 |
0 1 0 1 |
1 1 1 0 |
АБО-НЕ (функція Пирса) |
|
0 0 1 1 |
0 1 0 1 |
1 0 0 0 |
Будь-яку логічну функцію можна записати з допомогою елементарних логічних функцій. Відповідні схеми цифрової техніки, які реалізують ці функції, називаються логічними елементами цифрових схем. З їх допомогою можна описувати роботу і проектувати структури цифрових пристроїв. Вони перетворюють вхідні сигнали, які з’являються на їх входах, в вихідні.
Серед логічних елементів виділяють універсальні набори, з допомогою яких можна реалізувати логічну функцію будь-якої складності. Такі набори називають функціонально-повними логічними базисами. До цих базисів відноситься набір логічних елементів, який складається з елементів НЕ, І, АБО, а також констант 0 і 1. Він на сьогодні є найбільш поширеним.
Цей базис називається булевим, тому що його вперше дослідив англійський вчений Буль. Розглянемо нижче цей базис. В більшості випадків константа 1 реалізуються в ньому з допомогою деякого значення фізичного параметру, а константа 0 – відсутністю цього значення, хоча можливе й зворотне кодування.

 Послідовний
пристрій
Послідовний
пристрій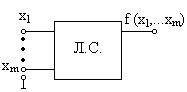 Паралельно-послідовний
пристрій
Паралельно-послідовний
пристрій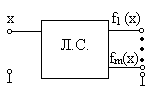 ослідовно-паралельний
пристрій
ослідовно-паралельний
пристрій