Лабораторная работа № 42 изучение интерференции в опыте с бипризмойфренеля

Цель работы –изучение интерференции света в опыте с бипризмой Френеля. Определение длины световой волны и преломляющего угла бипризмы.

1. Теоретические основы работы

Интерференциейназывают явление перераспределения энергии световых волн в пространстве, возникающее при наложении двух или более когерентных волн. В результате интерференции возникает картина, представляющая собой чередование максимумов и минимумов интенсивности света. Устойчивая во времени интерференционная картина наблюдается при наложениикогерентныхволн. Волны называются когерентными, если разность фаз колебаний, возбуждаемых этими волнами в данной точке пространства, с течением времени не изменяется. Когерентными являются толькоквазимонохроматическиеволны, у которых амплитуда, частота и начальная фаза остаются постоянными за время наблюдения.

Две когерентные волны можно получить двумя способами – делением фронта исходной волны и делением ее амплитуды. И в том и в другом случае исходную волну разделяют на две (которые являются когерентными), организуют разность хода и затем сводят их в месте в некоторой области пространства. В результате в этой области возникает интерференционная картина. Важно отметить, что качество наблюдаемой интерференционной картины существенно зависит от степени монохроматичности излучения. Так в белом свете, имеющим сплошной спектр, наблюдение интерференционной картины практически невозможно из-за того, что максимумы интерференции для одних длин волн накладываются на минимумы интерференции для других длин волн. Поэтому интерференционные Катрины обычно наблюдают в квазимонохроматическом свете, который получают из белого света с помощью светофильтров.

Одним из приборов, с помощью которого осуществляется деление фронта волны на две части, является бипризма Френеля. Принципиальная схема наблюдения интерференционной картины при помощи бипризмы Френеля показана на рис. 1. Бипризма Френеля представляет собой изготовленные из одного куска стекла две симметричные призмы 1, имеющие общее основание и малый преломляющий угол. На расстоянии от бипризмы в воздухе располагается либо ярко освещенная щель, устанавливаемая параллельно ребру бипризмы, либо точечный источник света S (см. рис. 1).

Можно показать, что в случае, если преломляющий угол призмы мал (а это так и есть) и лучи падают на призму под небольшими углами, все лучи отклоняются призмой практически на одинаковый угол j

, (1)

где n – показатель преломления стекла, из которого изготовлена призма; θ – преломляющий угол призмы. В результате преломления света бипризмой фронт волны делится на две части, причем каждая из них отклоняется к оптической оси. В результате, после прохождения светом бипризмы, образуются две когерентные волны, которые накладываются друг на друга в некоторой области пространства, которая называется полем интерференции. Лучи, преломленные каждой из половинок бипризмы, кажутся выходящими из двух мнимых источников S₁ и S₂, которые находятся в одной плоскости с реальным источником света S. Как видно на рис. 1, расстояние d между мнимыми источниками:

(2)

Рис. 1. Схема наблюдения интерференционной картины

с помощью бипризмы Френеля

Интерференционную картину наблюдают на экране Э, расположенном в поле интерференции. Интерференционная картина имеет вид чередующихся параллельных светлых и темных полос. Ширина интерференционной картины H определяется шириной поля интерференции и зависит от расстояния экрана от бипризмы.

Рассчитаем интерференционную картину, полученную с помощью бипризмы Френеля. Для определения оптической разности хода рассмотрим рис. 2. Здесь r₁ и r₂ – геометрические пути волн от соответствующих мнимых источников в точку наблюдения. Оптическая разность хода (, среда однородная– воздух).

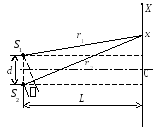
Рис. 2. К расчету координат интерференционных минимумов и максимумов

Произведение геометрической длины пути r, которую волна проходит до точки наблюдения, на показатель преломления среды n называется оптической длиной пути в среде с показателем преломления n, а величина , равная разности оптических длин проходимых волнами путей, носит название оптической разности хода.

Условием интерференционных минимумов является соотношение:

D = ± (2m + 1) l/2 (m =0, 1, 2, .....) , (3)

где l – длина световой волны в воздухе.

Для нахождения координат интерференционных минимумов найдем зависимость оптической разности хода Dот координатыxна экране2. Из рис. 2 (для упрощения рисунка бипризма на нем не изображена) следует что

(4)

^, (5)

где r₁ и r₂ –геометрические пути света от соответствующих мнимых источников; L – расстояние от источника S до экрана; d – расстояние между мнимыми источниками; x – координата точки наблюдения (см. рис. 2). Вычитая (4) из (5), получаем:

(6)

Положим, что L >> d, тогда , а. С учетом этого из (6) получаем оптическую разность хода:

. (7)

Приравнивая правые части уравнений (3) и (7), получим координаты минимумов интенсивности:

(8)

Из условия интерференционного максимума

D = ± k l/2 (k =0, 1, 2, .....) (9)

и соотношения (7) получим координаты максимумов интенсивности:

(10)

Назовем расстояние между двумя соседними минимумами интенсивности интерференционной картины шириной интерференционной полосы, а расстояние между двумя соседними максимумами интенсивности расстоянием между интерференционными полосами Dx. Тогда из формул (8) и (10) следует, что ширина полосы и расстояние между полосами имеют одинаковое значение, равное

(11)

Из (11) можно определить длину световой волны l, если измерить расстояние между интерференционными полосами (либо ширину интерференционной полосы) Dx, расстояние d между мнимыми источниками S₁ и S₂ и расстояние L от мнимых источников до плоскости формирования интерференционной картины (экрана):

. (12)

Используя экспериментальные данные, можно определить также преломляющий угол бипризмы. Из (1) и (2) с учетом того, что при малых углах преломления , получаем

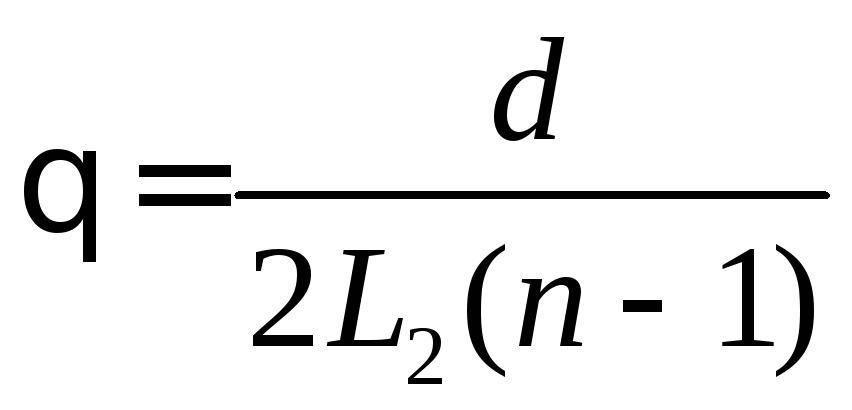, (13)

где d – расстояние между мнимыми источниками; L₂- расстояние от плоскости, в которой расположены мнимые источники, до бипризмы; n – показатель преломления стекла бипризмы.

Для определения расстояния d между мнимыми источниками, входящего в формулу (12), необходимо с помощью собирающей линзы (рис. 3) получить изображение на экране мнимых источников и. Затем нужно измерить расстояниемежду ними и с учетом увеличения линзы получить, что

. (14)

Рис. 3. К расчету расстояния между мнимыми источниками

Расстояния a и b измеряются при помощи линейки, закрепленной на оптическом рельсе стенда; расстояние – с помощью шкалы, нанесенной на экран.