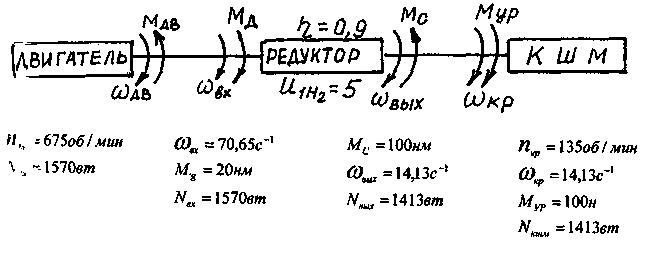3. Задания на контрольную работу

Студенты третьего курса специальности 160901 заочного обучения по дисциплине «Теория механизмов и машин» выполняют одну контрольную работу на тему «Исследование сложного зубчатого механизма».

При выполнении контрольной работы должны быть соблюдены следующие требования:

1. Контрольная работа должна строго соответствовать выбранному варианту.

2. Графическая часть работы аккуратно выполняется на листе формата АЗ или на листе миллиметровой бумаги (кроме синей) формата АЗ.

3. Пояснительная записка пишется четким почерком на листах формата А4. Решение должно сопровождаться краткими, ясными пояснениями, ссылками на применяемые законы и уравнения, изложение допускается вести в безличной форме. Формулы, встречающиеся в пояснительной записке, должны быть расположены отдельными строками. Структура титульного листа пояснительной записки приведена ниже.

4. Вычисление следует производить с точностью до двух значащих цифр после запятой.

5. Перед решением задачи в пояснительной записке записываются ее условия с числовыми данными, вычерчивается схема механизма без масштаба. На листе формата АЗ все чертежи выполняются в масштабе.

П ри решении задачи необходимо выполнить:

1. Определить тип редуктора, его применимость.

1. Аналитически и графически определить передаточное отношение редуктора.

2. Определить основные характеристики планетарного редуктора, исходя из условий сборки, соседства, соосности (если в схеме планетарных редукторов больше одного - то основные характеристики выполнить для каждого планетарного редуктора). Число сателлитов «р» выбрать, исходя из величины передаточного отношения.

3. Выполнить силовой расчет редуктора. Считать колеса редуктора нулевыми. Модули колес принять равными т = 1 мм. или т = 1,5 мм. или т = 2 мм. План зубчатого механизма вычертить в масштабе.

5. Осуществить проверку правильности выполнения силового расчета по равенству мощностей на входе и выходе редуктора.

{Мвх-сдвх = Мвых -СОёых) при /I =1,

где ^ - коэффициент полезного действия редуктора.

6. Определить коэффициент полезного действия (КПД) редуктора.

7. Определить мощность и число оборотов двигателя.

8. В общем виде вычертить схему привода кривошипно -шатунного механизма (КШМ), определив и обозначив кинематические и силовые характеристики на каждом валу схемы.

Во время экзаменационной сессии студент выполняет лабораторную работу, защищает проверенную преподавателем контрольную работу, сдает дифференцированный зачет по всему курсу, содержание которого представлено на страницах 4-6 данного пособия.

Номер задания студент выбирает по приведенной ниже таблице 2 в соответствии с первой буквой своей фамилии.

68

Таблица 2

Начальные	г——— —	Частота вращения		Момент
буквы	№	(число оборотов)	Направление	сопротив-
фамилий	задания	на выходе	вращения	ления на
студентов		из редуктора,	выходного	выходном
		/2- , об/мин	вала	валу, Мс, нм
1 А	1	250	по часов.стр.	40
Б	2	390	против час.	60
В	3	НО	по часов.стр.	80
Г	4	170	протвдчас.	100
Д	5	420	по час. стр.	50
Е	6	140	против час.	70
Ж	7	200	по час. стр.	90
3	8	180	против час.	150
и	9	300	по час. стр.	130
к	10	320	против час.	110
л	11	160	по час. стр.	200
м	12	220	против час.	190
н	13	120	по час. стр.	140
О	14	230	против час.	120
п	15	250	по час. стр.	170
р	16	270	против час.	160
с	* 17	100	по час. стр.	180
т	18	130	против час.	210
У	19	150	по час. стр.	250
ф	20	170	против час.	240
X	21	190	по час. стр.	230
ц	22	290	против час.	220
ч	23	310	по час. стр.	75
ш	24	330	против час.	85
щ,э	25	350	по час. стр.	95
ю	26	400	против час.	115
я	27	380 —	по час. стр.	125

I

4. Пример выполнения контрольной работы

Исходные данные: схема зубчатого механизма (рис. 37), числа зубьев колес

21 =80 2₂ = 30 2₃ = 20

2, = 16 2₅ = 16 2₃' = 48.

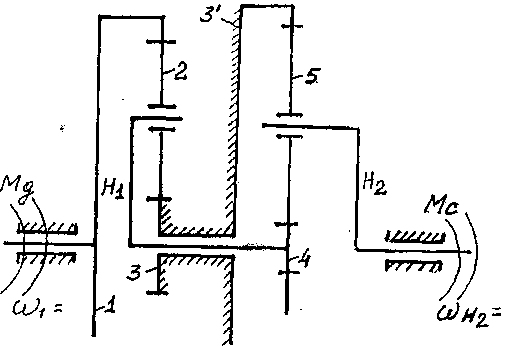
Направление вращения тихоходного вала на выходе редуктора (вала водила Н₂) - по часовой стрелке, (л)цг.~ 14,13 с"¹; что соответствует /г,^ = 135 об/мин. Момент сопротивления на тихоходном (выходном) валу редуктора М„₂ = М_с = 100 нм. Определить: провести исследование сложного зубчатого механизма.

1. Определить тип редуктора.

Данный редуктор - сложный планетарный механизм, состоит из двух планетарных редукторов, т.к. в каждом редукторе есть солнечное колесо (1 и 4), сателлиты (2 и 5), опорные колеса (3 и 3) и водила (Н₁ и Н₂). Первая ступень - редуктор Джемса, вторая ступень - тоже редуктор Джемса, Сочетание этих двух редукторов может быть применено в силовой быстроходной передаче.

Рис. 37. Схема многоступенчатого зубчатого механизма

2. Аналитически и графически определить передаточное отношение.

а) Аналитически:

".«.=1-«»^,, = 1-^— -—1 = ¹⁺— = 1 + |? = 1 + 0,25 = 1,25; ^{т п} 2, 2₂] 2, 80

^4Нг ° [ 2₄ 2_Ь\ 2, 16

И_|Я2 =1,25-4 = 5.

б) Графически:

Чертим план зубчатого механизма. Выбираем модуль колес, принимаем т = 1,5 мм и определяем размеры колес для зубчатого механизма.

г, = 80; </, = т%, = 1,5 • 80 = 120мм \ г, = 0,06.и;

г₂ = 30; с1₂ = /и2, = 1,5 • 30 = 45мм; г, = 0,0225.м \

2_Э=20; (/₃=/и2з=1,5-20 = 30.ш<; г₃=0,015.«;

2„=1б; (/₄=ш2₄=1,5 16 = 24л(.и; г, =0,012.«;

г ,=48; ₁/,=т2,=1,5-48 = 72д|.и; л=0,036.и;

ззз з

г₅=1б; ^₅=т2₅ =1,5-16 = 24.1ш; /-₅=0,012л*.

Тогда А =——— =-7-г-= 0,001 м/мм. гогда ^ «, РА(герт) 60

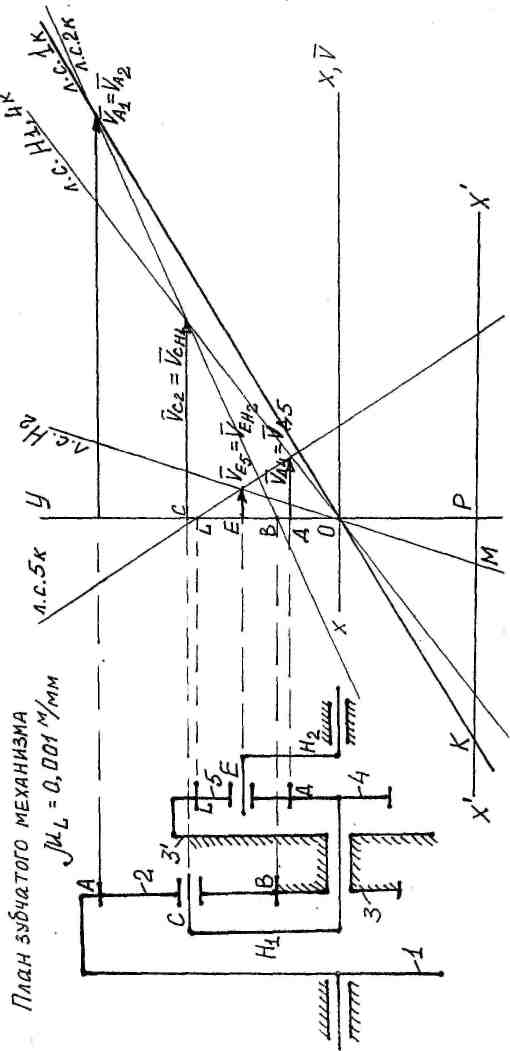
Для вычерченного в масштабе зубчатого механизма строим план

скоростей (рис. 38).

Выбираем систему координат УОХ, в которой откладываем произвольный вектор скорости точки А колеса 1-1^^, через конец вектора Щц и точку О проводим линию скоростей 1 колеса (л.с. 1 к). В точке А Ци* ?_Аг. %% - вектор окружной скорости сателлита 2. В точке «В» находится мгновенный центр скоростей сателлита 2, через конец вектора и точку «В» проведем линию скоростей сателлита (л.с. 2 к). В точке „С скорость сателлита 2 и скорость водила Н, совпадают, проведем из точки С вектор 7сг = %щ Д° пересечения с линией скоростей сателлита. Через конец вектора У_Сщ и точку О проведем линию скоростей водила (л.с. Н,), которая является одновременно линией скоростей колеса 4,

¹

о о

Ц

■4!

Найдем на этой линии скорость точки Д колеса 4 - у,_и = Уд₅. Колесо

5 - сателлит, мгновенный центр скоростей которого находится в точке I, поэтому через конец вектора скорости точки Д₄ и точку Ь проведем л.с.бк - сателлита 5. В точке Е скорость колеса 5 - сателлита и водила Н₂ совпадают Ур.ь=У_е._нг, поэтому из точки Е проведем вектор скорости до пересечения с л.с.бк, получим вектор скорости водила у_Е„₂ , через конец вектора у_Ен2 и точку О проведем л.с.Н₂.Ллан скоростей построен. Для определения передаточного отношения на произвольном расстоянии ОР параллельно оси х - х проводим линию х' - х' , которая пересекает л.с.1к в точке К и л.с.Н₂ - в точке М. Передаточное отношение

^и» МР \\,5мм

Знак передаточного отношения положительный - отрезки КР и МР лежат в одной четверти.

3. Определить основные характеристики редуктора:

а) условие сборки:

- для редуктора 1 — 2 — 3 — Н1

г,+г_г=кр; 80+20 = 254. Берем 4 сателлита, в этом случае условие сборки соблюдается.

- для редуктора 4 - 5 - 3' - Н₂

г,+2_г,=КР; 16 + 48 = 16-4,

р = 4, в этом случае условие сборки соблюдается.

б) условие соседства:

- для редуктора 1-2-3 -НЬ

1. (г, -г₂Ут7Г/р^.2₂+2 - внутреннее зацепление

(80-30)5т180°/4 >30+2

50-0,71 > 32 - условие соблюдается.

2. (2₂+г₃)зтж/р^г₂+2

(30 + 20)зт180°/4 > 30+2

500,71 > 32- условие соблюдается.

- для редуктора 4 - 5 - 3' - Н₂

1. \2,-г₅)вт7Г/р^г_$+2 - внутреннее зацепление

(48-1б)ып180'74 > 16+2

320,71 > 18 - условие соблюдается.

2. (г, + 2₅)8шл/р>2₅ +2 -внешнеезацепление (16+1б)8ш180°/4 > 16+2

320,71 > 18 - условие соблюдается.

в) условие соосности:

- для редуктора 1—2-3 -Н!

2) + 2₂ = 2, — 2₂ 20 + 30 = 80-30

50 = 50 - условие соблюдается.

- для редуктора 4 - 5 - 3'- Н₂ - 7и + 2₅ = 2з< - 2-5 или 16 + 16 = 48 - 16; 32 = 32 - условие соблюдается.

Таким образом, условия сборки, соседства и соосности для обеих зубчатых механизмов (редукторов) соблюдаются при р = 4. 4. Выполним силовой расчет редуктора.

Силовой расчет редуктора заключается в определении усилий в зацеплениях, усилий на валах и усилий в подшипниках водила. Силовой расчет проводим без учета КПД редуктора, т.е. при ф, *' 1.

а) Вычерчиваем в масштабе план сложного зубчатого механизма (рис. 39). Предположим, направление вращения водила Н₂ - по часовой стрелке (отмечаем на чертеже, рис. 39), тогда направление момента сопротивления М_с на валу водила Н₂ - в противоположную сторону (момент сопротивления всегда направлен в сторону, противоположную направлению со , в данном случае (л)н_г )■ Знак передаточного отношения зубчатого механизма положительный, значит направление вращения вала на входе в редуктор (00^ ) совпадает с направлением вращения вала ведомого водила (СОщ )• направление вращения вала колеса 1 отмечаем на чертеже, рис. 39. Направление движущего момента (М_д - на валу колеса 1) всегда совпадает с направлением вращения ведущего колеса (отмечаем направление М_э на чертеже, рис.39).

б) Определяем СОх и М_э на входе в редуктор _м ,₀₀

Ш& *й)4 ъШщг&шж* 14,13-5 = 70,65 6"'; М_вх= М_д=^-=-т^?-20нм.

в) Силовой расчет планетарного редуктора - нужно всегда начинать с солнечного колеса, в данном случае - это колесо 1 - ведущее. Колесо 2 - сателлит - ведомое и ведущее, колесо 3 — условно ведомое.

1. В масштабе^ = -—;—\⁼^~ = 0,0015 м/мм вычерчиваем

план колес 1-2 (рис.40). В редукторе 1-2-3-Н! имеется четыре симметрично расположенных сателлита, поэтому движущий момент равномерно распределяется между всеми сателлитами. Расчет ведется по одному сателлиту, поэтому М$ - -Ц& - 4г - &^нм-

Силы взаимодействия колес 1 и 2 приложены в точке Р (полюс зацепления) и направлены по нормали к профилям зубьев (по линии зацепления ММ), угол зацеплениям^ 20. Сила Р₁₂ сила реакции со стороны ведущего колеса 1 на ведомое колесо 2. Сила Р₂₁ - сила реакции со стороны ведомого колеса 2 на ведущее колесо 1.

Положение нормали NN определяется правилом:

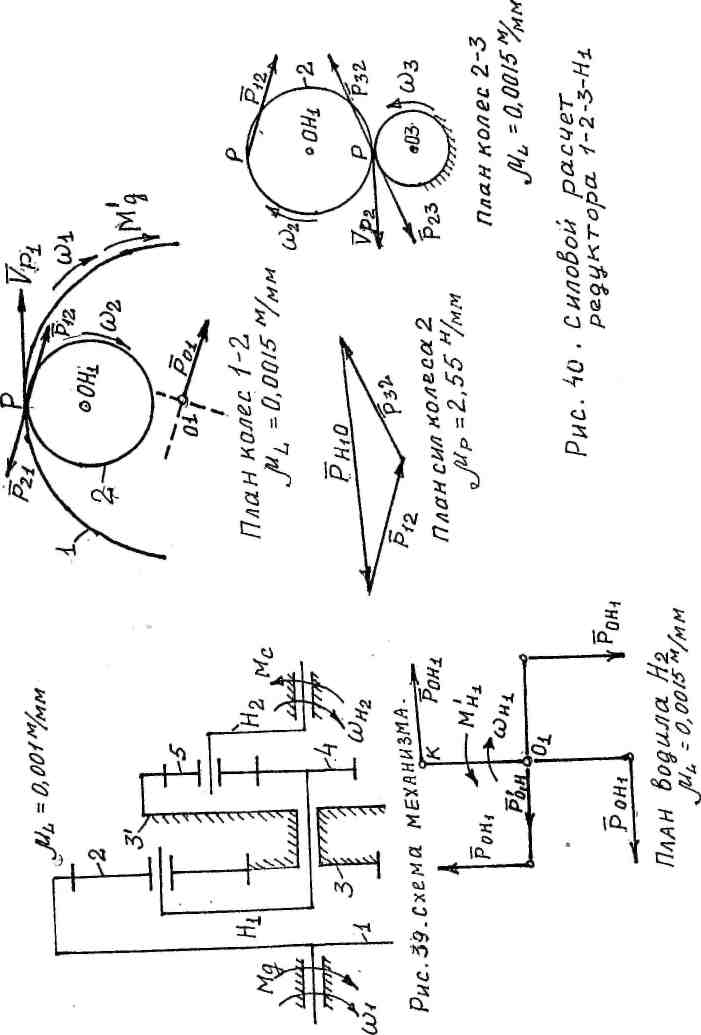
если ведущим является колесо с внутренним зацеплением, то поворачивая вектор окружной скорости у_Р, на угол сс₀ (а₀=20°) по направлению угловой скорости ведущего колеса, получим положение нормали N - N и вектор силы реакции ведущего колеса на ведомое (?|₂). Вектор ?21 = -?12.

Рассматриваем равновесие колеса 1. Колесо 1 находится в равновесии под действием силы ~р_и, момента м\ и реакции на валу Лн. 3>₀,(?)=о,

Р₂₁-А-Л^=0

м\

А = —'-; к = к • сов 20° = 0,06 • 0,94 = 0,056л<;

^/>"⁼ в⁼⁸⁹'³"^{; Ря =} ~^ла''" ^{= 89,зм} ■

/>21 + Яш = 0; Р_гх = -Р_т , Р₀₁ = 89,3н.

2. В масштабе 0,0015 м/м вычерчиваем план колес 2-3 (рис. 4#). В точке Р определяем положение нормали NN по правилу: если ведущим является колесо с внешним зацеплением (колесо 2), то поворачивая вектор окружной скорости точки Р у_п на угол а„ (а_ш =20°) против направления вращения угловой скорости ведущего колеса а>_г, получим положение нормали N - N и вектор силы реакции ведущего колеса на ведомое (здесь условно ведомое колесо 3) ?₂₃, ?и = -?₃₂.

Рассматриваем равновесие колеса 2 (сателлита)

Здесь а, = й₂ =г₂ -сова, значит|А₃₂|=|;;₂|. и р₃₂ =89,зя.

Графически решаем это уравнение, т.е. строим план сил, который должен быть замкнут (рис. 63).

89 3

Масштаб плана сил ц_Р = -—=- = 2,55н/лш.

^' 35 Р_н„=Рн,о р,_е =65-2,55 = 165,75», Р =-Р

^г Я,0 ' ОН, '

3. В масштабе 0,0015 м/мм строим план водила (четыре ветви).

О_гК = г₂+г_} = 0,0225м + 0,015м = 0,0375м. О 0175

На чертеже о.к = '±^± = гъмм.

^г ' 0,0015

Рассматриваем равновесие одной ветви водила. Одна ветвь водила находится в равновесии под действием силыр_()Я , м'_н и р_он.

^м'н = ^рон, ■ 0,К = 165,75н-0,0375м = 6,21нм.

^]? = 0, Рон, +~Ро,н =0, Р~он, =-Ро_хн, Рон, = 165,75н.

Как видно из чертежа, каждая ветвь водила имеет реакцию со стороны вала ?₀,« = Ш,75», и суммарная реакция со стороны вала равна нулю, значит вал водила уравновешен.

Для остальных ветвей водила расчет тот же, поэтому момент на

Валу ВОДИЛа Н, равен М„ = м'„ 4 = 6,21-4 = 24,84км.

Этот же момент действует на валу колеса 4, т.е. м„ =м_н и со„ = со_л.

4. Проводим силовой расчет редуктора 4 - 3' - 5' - Н₂, рис. 4 т. Отметим, вал водила Н1 и колеса 4 находится в равновесии, поэтому м_н, =-М<, или по другому: водило (-Ц для редуктора 1 - 2 - 3 - И^

является ведомым, а колесо 4 для редуктора 4 - 5 - 3' - Н₂ ведущим, поэтому направление вращения со, (по часовой стрелке) совпадает с направлением момента м„.

- В масштабе ц₁ =о,оо\м1мм вычерчиваем план колес 4-5, отметим, колесо 4 - ведущее, колесо 5 - сателлит - ведомое.

Рассмотрим равновесие колеса 4. В редукторе четыре симметрично расположенных сателлита, поэтому М4=л/,/4=24,84/4 = б,21нл<.

Колесо 4 находится в равновесии под действием силы я», момента м\ и силы ?<м. 5>„(р)=°. Р»к-м\=о,

Л = г₄со820° = 0,012-0,94 = 0,0113^,

^=^ = -^_ _{= 5}49,55„, Н 0,0113

Л* =-/"«. Л₅=549,55н.

1?=_о,

Р»+Р04=0, Р₅₄=-Р„,

/> =549,55н.

Рис. И Силовой расчет _{

рЕДУНТООА ^-5-3 ~Н2.

Рассматриваем равновесие колеса 5 - сателлита. Сателлит 5 находится в равновесии под действием сил р₃'5, ?« и силы действия водила Н₂ на сателлит 5 р~н₂о . 2>„(?)=о, р„ь,-р,;Н,=о,

Р, = р = 549,55н.

3 5 45 ' ,

/⁵з^,5+Р45 + Ря₂о = о, решаем это уравнение графически.

Строим план сил в масштабе/^ =—— = 18,з«/лш и определяем р„₁₀,

Р_Иг0 ттф, = 6018,3 = 1098н.

- В масштабе //, =ШИ= °'^0П+0'^Ш =о,ооо!м/мм строим план ^л1 ОА 35

водила Н₂ (4 ветви).

Рассмотрим равновесие одной ветви водила. Ветвь водила

находится в равновесии под действием сил р_он , р'_он и момента м'„ .

2>.(?)=о, м'_Н1-р_он^н = о,

й = 0,024-сое 20°,

Л^, = 1098 • 0,024 • 0,94 =24,77™.

Для остальных ветвей водила расчет тот же, поэтому момент на валу водила Н₂ равен

М„ =М_Н ■4 = 24,77-4 = 99,0&нм*100нм.

н₂ н_г

Отметим направление момента м„ , угловая скорость совпадает с

направлением момента и угловой скорости на выходе из редуктора, определенного по заданному направлению угловой скорости.

Проверяем правильность расчетов. Составим уравнение мощности на входе и выходе редуктора (энергетическое равенство),

М₁Ф_х=М_нСО_н, при УСЛОВИИ 77 = 1. М,Ц_Н2=М_Н2. 20нм ■ 5 = Шнм. В

расчете получили м_нг =99,08км. Процент ошибки 0,9 %. Расчет проведен верно.

5. Определяем КПД редуктора.

Ч\Н_г ⁼Ч\И_Х 'Ч4Н_г ■

^ш,=^-[1-?7'(1-",я)].

и_щ =1,25; 77'=0,95 •0,95 = 0,9,

7.я, =^[1-0,9(1-1,25)1=0,98,

Чщ =7Г-[¹-^;7'(1-",«)]=1[1-0.9(1-4)] = 0,92,

^И4Н₂ ⁴

Ц_щ =0,98 0,92 = 0,9.

6. Определяем мощность на выходе из редуктора, мощность на нходе в редуктор, мощность и число оборотов двигателя.

- мощность на выходе из редуктора равна мощности необходимой для преодоления сил сопротивления в кривошипно- шатунном механизме, по данным мощность кшм равна

Яъш^Фщшт, -Му,, = 14,13100 = 1413вт

Значит мощность на выходе из редуктора л^ =1413вот.

- мощность на входе в редуктор определим с учетом КПД, югда лг„ -Д-.-Шыявв. Ы+'ПчИ^

77 °'^у

- мощность двигателя совпадает с мощностью на входе в I аддуктор, тогда ы_л = #„._Л = 1 т_вт.

Число оборотов двигателя равно числу оборотов на валу входа в

родуктор.

^по, ^=п«._р. *Л«й..^>Ц»₁ =135-5 = 675об/л<ин.

7. Вычерчиваем схему привода КШМ с учетом направления нращения валов и силовых характеристик на каждом валу схемы.