2.4.4. Условия сборки, соседства, соосности планетарных механизмов

При проектировании планетарного редуктора с заданным передаточным отношением необходимо выполнение условий: соосности, соседства, сборки.

Условие соосности. Это условие, при котором оба центральных зубчатых колеса и водило должны иметь общую геометрическую ось вращения. Это условие может быть записано: 2, +г₂=2₃-2₂ для схемы 1 - редуктор Джемса; 2, +2₂ = 2₃ -г, для схемы 2 - редуктор со сдвоенными сателлитами; 2, +2₂ = 2,+2₂, для схемы 3 - редуктор Давида; 2, - г₂ = 2, - 2, для схемы 3 - редуктор Давида.

Условие соседства. Это условие, при котором все сателлиты, размещенные в одной плоскости, равноудалены и не задевают друг друга. Условие записывается в виде неравенства: (г, +2₂)иттг/р > 2₂ +2 - для внешнего зацепления (тг= 180°);

р - число сателлитов. [2,-2 ,}зшЯ7/?>2 ,+2 - для внутреннего зацепления.

Условие сборки. Это условие, при котором зубья всех промежуточных колес (сателлитов) могут войти в правильное зацепление с зубьями центральных колес 1 и 3 . Условие выражается:

1. Для редуктора Джемса (схема 1):

2,+2₃=кр, где Р - число сателлитов; К - любое целое число.

2. Для остальных редукторов (схема 2, 3):

2 2

ц„ --^- = к-р', где: р' - число блоков сателлитов; Э - наибольший

общий делитель чисел 2, и 2,; К-любое целое число.

В силовых планетарных редукторах применяют, возможно, большее число сателлитов, чтобы уменьшить нагрузку на каждую пару зубьев. Максимальное число сателлитов зависит от передаточного отношения: При: н,„=15 Р_т„=з

И,„=7 Я_пю=4

И,я=4 С =6-7

Пример 1.

Проверить условия соосности, соседства, сборки для редуктора Джемса (рис. 26), число зубьев 2, = 20 и 2₂= 36.

Определяем число зубьев опорного колеса по условию соосности:

2 0 + 36 = 2,-36, 2₃=92.

Определяем передаточное отношение редуктора Джемса:

7 47

и_ш=\ + =± = 1 + — = 5,6. '" 2, 20

В зависимости от, передаточного отношения выбираем число сателлитов: р=4. Проверяем условие соседства:

а) (г, +2₂)зтШ°//> > 1_г +2 - для внешнего зацепления,

(20 + Зб)зт180°/4 > 36 + 2,

39,59 > 38 - условие соблюдается;

б) (г_г-2₂)этт°/р>2 +2 -для внутреннего зацепления,

(92-Зб)8ш180°/4 > 36 + 2,

39,59 > 38 - условие соблюдается.

Проверяем условие сборки:

2,+2₃=к-р,

20+92 = к-4, 112 = 28-4 - условие соблюдается.

Пример 2.

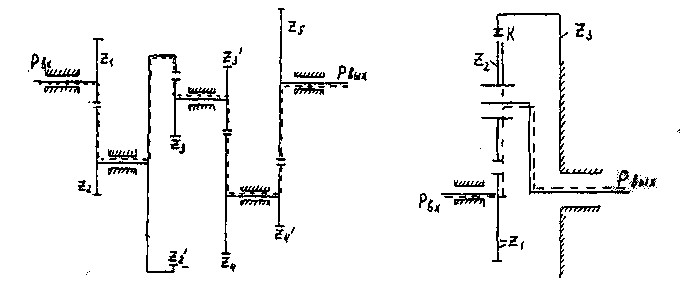
Проверить условия соосности, соседства, сборки редуктора со сдвоенными сателлитами (рис. 25), числом зубьев 2₄=20, 2₅ =40, 2₆ =80. Определяем число зубьев колеса 5' по условию соосности:

2< + 2₅=2₆-2_$,, 20 + 40 = 80-2₅,, 2₅,=20.

Определяем передаточное отношение редуктора со сдвоенными сателлитами:

и_{4н =1}3^=1+^°=9.

^4Н' 2,2₅. 20-20

В зависимости от передаточного отношения выбираем число блоков сателлитов р' = 3. Проверяем условие соседства;

а) (2₄ +2₅)8т180°/з > 2₅ + 2 - для внешнего зацепления,

(20 + Зб)₈ю60° >40 + 2,

51,9 > 42 - условие соседства выполняется;

б) (2₆-2,)зт180^о/з>2, + 2 -для внутреннего зацепления,

(80-20)8Н1бО° > 20 + 2,

51,9 > 22 - условие соседства выполняется.

Проверяем условие сборки:

9-20-20/п = к-з, 9-400/200=6-3 - условие сборки выполняется.

Пример 3.

Проверить условия соосности, соседства, сборки редуктора Давида (рис.24), с числами зубьев г, =30, г₂=18, 2₂,=20, 2₃ =28.

Проверяем условие соосности:

30 + 18 = 20 + 28, 48 = 48 - уСЛОВИв СООСНОСТИ ВЫПОЛНЯвТСЯ.

Определяем передаточное отношение редуктора Давида: _Мш=1_ад₌₁_1^₌о_;84.

2,2₂. 30-20

Редуктор Давида - это не силовой редуктор, т.е. большую мощность через редуктор передать нельзя, поэтому число блоков сателлитов равно р' = 3.

Проверяем условие соседства:

а) (2, +г₂)81п180°/з > 2₂+2 - для внешнего зацепления,

(30+18)зшб0° > 18 + 2,

41,76 > 20 - условие соблюдается.

б) (г₃+2:₂,)5т180^о/з>2₂, + 2 -для внешнего зацепления,

(28 + 20)зт60° > 20 + 2,

41,76 > 22 - условие соблюдается.

Проверяем условие сборки:

2,2,

0,84.30-20/Х) = >(:-3, 0,84-600/6 = 28-3,

84 = 84 - условие сборки соблюдаются.

2.4.5. Коэффициент полезного действия зубчатых передач

Потери мощности в зубчатых передачах складываются из потерь:

на трение в зацеплении,

на трение в подшипниках,

из гидравлических потерь на размешивание и разбрызгивание масла.

КПД простой передачи вычисляется:

где: Т]_г - КПД зубчатой передачи:

7з = 0,95+0,98 -для цилиндрической ступени;

7з = 0,96+0,97 - для конической ступени;

Т]_ъ = 0,7+0,9 - для червячной ступени.

Г\_п- КПД, учитывающий потери в одной паре подшипников:

77„= 0,99+0,995 - для подшипников качения;

7]„ = 0,97-0,99 - для подшипников скольжения;

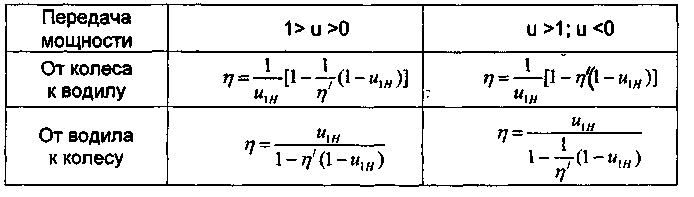
т - число пар подшипников в передаче;

г/_г- КПД, учитывающий гидравлические потери, связанные с перемешиванием и разбрызгиванием масла в корпусе передачи (Т]_г = 0,97-0,98).

В многоступенчатом зубчатом ряде передача мощности от ведущего колеса к ведомому осуществляется последовательно, цепочкой (рис.

27>

Рис. 27. Поток мощности в многоступенчатой передаче

Рис. 28. Поток мощности в планетарной передаче

Таблица 1

В планетарной передаче поток мощности на солнечном колесе 1 разветвляется и идет на сателлиты (рис. 28')- С каждого сателлита часть мощности идет к опорному колесу, часть - на водило. На валу водила мощность с потерями собирается от всех сателлитов. У опорного колеса [(•)к] часть мощности теряется. Поэтому КПД планетарного механизма можно вычислить по формулам табл. 1.

В таблице 1. ц' - КПД обращенного планетарного механизма, полученного путем остановки водила.

Если при передаче движения от колеса к водилу значения передаточного отношения и^ лежат в пределах 0 < и_1н<1-т|' или 0 > и_1н>1-1/ ц', то КПД планетарного редуктора будет отрицательным. Это означает самоторможение, т.е. передача движения от колеса к водилу невозможна. При передаче движения от водила к колесу КПД планетарного механизма всегда больше нуля и самоторможение в этом случае не может иметь места, но при и_1н-> 0, ц -> 0.

Пример.

Определить КПД сложного планетарного механизма, представленного на рис. 25- Число зубьев механизма: 2! = 20, 2₂=36, 2₃ = 92,

24 = 20, 2₅ = 40, 2₆ = 80, 2₅'=20.

а) Н_т. = 5,6 (определено ранее).

При передаче мощности от колеса 1 к водилу Н1 и условии и_щ >1

выбираем формулу для определения г|1_н1 (см. табл. 1).

Пая = Л--П'-П-"!„,,>/.

"|я,

тГ = Ли-Лаз = 0,95- 0,95 = 0,9.

^л=77[1-0,9(1-5,6)] = 0,92 5,0

б) и_ЛНг = 9(определено ранее).

При передаче мощности от колеса 4 к водилу Н₂ и при и^_г >1 выбираем формулу для определения гцнг (см. таблицу 1). Л4й, = Л-1 (1~ЩтМ*

^=^[1-0,9(1-9)] = 0,91

I

П' = -П.45 "Ли = 0.95 • 0,95 = 0,90, г,1Н2 = 0,92 -0,91= 0,84.