2.4.2. Планетарные механизмы

Планетарный механизм (рис. 22/^{состоит из} центральных колес 1, 3, сателлитов 2 и водила Н. Одно из центральных колес может быть неподвижно, например, колесо 3, оно называется опорным. Подвижное центральное колесо 1 называется солнечным. Сателлиты имеют подвижные геометрические оси. Траектория движения центров сателлитов (•) С - окружность. Сателлиты совершают сложное движение - вокруг собственной оси и вокруг центрального колеса 1. Подвижное звено, в котором помещены оси сателлитов, называется водилом. -. . _а

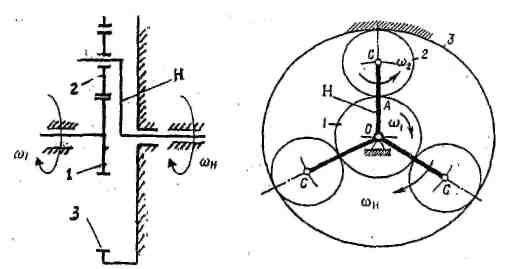
Рис. 22 • Планетарный механизм.

1 - солнечное колесо; 2 - сателлит; 3 - опорное колесо; Н - водило.

Планетарный механизм, как совокупность солнечного колеса, опорного колеса, сателлитов и водила, представляет собой одну ступень в более сложном и простом зубчатом механизме.

Зубчатые колеса при зацеплении образуют высшие кинематические пары. Низшими кинематическими парами являются подшипники, на которые опираются валы колес и водила. С кинематической точки зрения каждый вал может иметь один подшипник.

По формуле Чебышева степень подвижности планетарного механизма равна единице М = Зп - 2р₅ - р₄ = 3-3 - 2-3 - 2 = 1.

Это означает, что заданному повороту одного из его подвижных

звеньев (кроме сателлита) на входе соответствует строго определенный поворот звена на выходе. У планетарного механизма имеются несколько симметрично расположенных сателлитов. Их вводят с целью сокращения общих габаритов (снижаются усилия в зацеплении) и для разгрузки подшипников водила. Но при кинематических расчетах учитывают один сателлит, т.к. остальные в кинематическом отношении являются пассивными звеньями. Ведущим (ведомым) звеном планетарной передачи может быть как центральное колесо, так и водило.

2.4.2.1. Определение передаточного отношения планетарных механизмов

Передаточное отношение планетарных механизмов определяется двумя методами: аналитическим и графическим.

1. Аналитический метод (метод Виллиса)

Метод состоит в том, что механизму мысленно сообщается

дополнительное вращение (дополнительная угловая скорость), равное

по величине угловой скорости водила, но противоположное ей по

направлению Ы = _|й)_я|. Все звенья при этом получают приращение

угловых скоростей (+|-й>|), а водило останавливается. Механизм превращается в простую многоступенчатую передачу (рис. 23), и передаточное отношение обращгШэго механизма определяется обычными методами.

На основании этого метода окончательное выражение для определения передаточного отношения планетарного механизма имеет вид:

и -1-1/'"'

где: и_ш - передаточное отношение планетарного механизма от солнечного колеса к водилу;

и[^ - передаточное отношение обращенного механизм (рис. 23), т.е.

многоступенчатой передачи

^{13 к ;} г_гг₂ ж, следовательно

«.->-{-!)-*!■

(для планетарного механизма на рис. 22 )■

Формула Виллиса справедлива, если ведущим является солнечное колесо. Передаточное отношение от водила к колесу (т.е. если ведущим является водило) определяется равенством

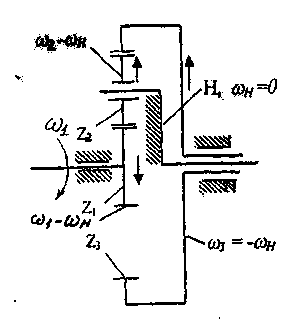
Рис. 23. Обращенный планетарный механизм

2. Графический метод Графический метод основан на использовании плана скоростей. Для построения плана скоростей используется ряд положений теоретической механики: _

• вращающееся тело имеет мгновенный центр скоростей: Г« =о;

• если цилиндр перекатывается без скольжения по поверхности, точка касания в данный момент имеет скорость У» = о.

• при отсутствии скольжения точки касания двух тел имеют одинаковые скорости;

• угловые скорости пропорциональны тангенсам углов наклона линии скоростей к линии радиусов (теорема Смирнова):

1₈а~со. Определение передаточного отношения графическим методом выполняют в определенном порядке.

План механизма вычерчивается в масштабе, вектор скорости

любого центрального звена задается произвольно, и план скоростей сводится к построению линий скоростей его звеньев (зубчатых колес). Практически поступают следующим образом (рис. 24):

• берут прямоугольную систему координат - обычно на центральной оси;

• задаются окружной скоростью любого центрального звена (солнечное колесо, водило), например, солнечного колеса, и изображают эту скорость вектором произвольной длины Щ, соединяя конец этого вектора с точкой на оси вращения колеса, имеющей окружную скорость, равную нулю (т. О), проводят линию распределения скоростей точек звена колеса 1;

- используем точку К, где скорости звеньев 1 (солнечное колесо) и 2 (сателлит) равны между собой У, = у₂;

- найдем мгновенный центр вращения блока сателлитов, им является точка А, значит в т. А у₂ =о. Для блока сателлитов имеем две скорости: Ул = о и у_к = У\ = У₂, через т. А и т. С проводим линию скоростей сателлитов;

- отметим: окружные скорости для сателлита и водила в точке М одинаковы V? = Уг = у_н- Вектор Ш выражает скорость точек 2 и 2' блока сателлитов, а значит, и скорость водила. Соединив конец вектора У_нс центром скоростей - т.О, получим линию скоростей водила;

-издОВС, ^«пропорционален Щ; изйОДЕ, 1%(5 пропорционален со_н

- на произвольном расстоянии ОР проведем прямую х'-х', параллельную линии х-х /.а = га,; а/3 = аД.

из ОР1_#Д=^,

из ОРИ «4~", тогда ^Л&ЛЗ^.

*"■ ОР '" _гф ОРР1 РЬ

то есть Ш_щ - отношение отрезков ^ и Р1, измеренное на чертеже в мм.

Знак передаточного отношения определяется так: если углы а, и Днаходятся по разные стороны от прямой ОР - то «и» имеет знак «-», если по одну сторону - то ни» имеет знак «+». В нашем случае «и» имеет знак «-», это значит, что ведомое звено (водило) вращается в противоположную сторону от вращения ведущего звена - солнечного колеса.

Для построения плана чисел оборотов (задано число оборотов колеса п,) выбирают удобный масштаб, в котором от произвольной точки О' откладывают отрезок 0"|, представляющий собой заданное число оборотов ведущего звена, через т. О' проводят к нему перпендикуляр О'Р, а через т. 1 - прямую, параллельную линии

скоростей солнечного колеса 1, через т. Р (пересечение прямых О'Р и 1Р) проводят лучи Р-Н, Р-2, параллельные линиям скоростей каждого звена (водила и сателлита). Отрезки О'Н, 0'2 пропорциональны числам оборотов

«„=от7//„; Ц,-~~, -»-53./4.

Передаточное отношение имеет знак минус, т.к. отрезки расположились по разные стороны от т. О'. Из плана чисел оборотов видно, что сателлиты и водило вращаются в одну сторону, солнечное колесо - в другую.

2.4.2.2. Типовые схемы планетарных механизмов

Схема 1

Редуктор Джемса.

Передаточное отношение определяется формулой:

И,„= 3 + 10. Знак передаточного отношения всегда положителен.

Схема 2

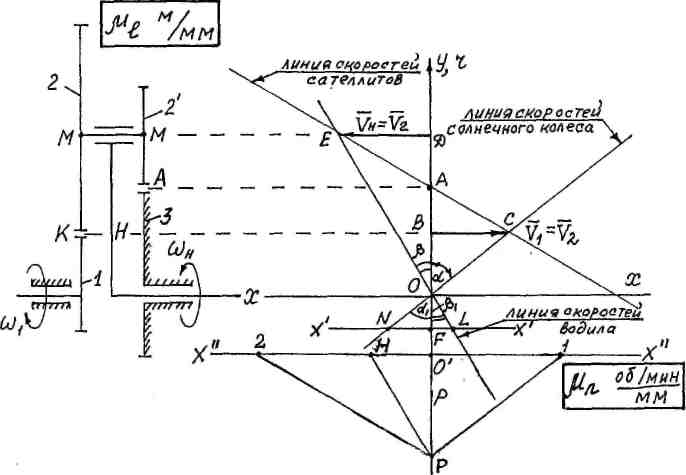
Схема 3

Редуктор со сдвоенными сателлитами.

Передаточное отношение определяется формулой:

Редуктор используется в

диапазоне «,„=7*25. Знак

передаточного отношения всегда положителен.

Редуктор Давида.

Передаточное отношение определяется формулой:

2,2,

Знак и$ может быть «+» и «-» в зависимости от отношения величин

зуЗбеа колес. Вели число зыВыВ колес тако&о, гто %*%&, -*1,

2, 2_г'

то Ичн-+0, Л и_Н1-+^со-

Рис. 24. План скоростей и план чисел оборотов планетарного механизма

Редуктор используетс передачах, так как КПД эти