Раздел 2. Расчет напряженного состояния толстостенной трубы в пределах и за пределами упругости

1. Расчетная схема и исходные данные

a = 20

b = 100

Труба находится в условиях плоской деформации, так как l>>d; где l – длина трубы, а d – диаметр трубы.

– модуль упругости;

Рисунок 2 – Расчетная схема

a

– модуль упругости;

–предел текучести;

– параметр упрочнения;

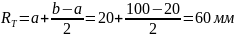– радиус, отделяющий область пластической деформации от упругой.

Труба находится под действием внутреннего давления . Для определения внутреннего давления соответствующего принятому значению RT воспользуемся формулой (39):

;

2. Расчет напряжений в пределах линейной упругости

Распределение напряжений вдоль свода трубы, в рамках линейной упругости следует из зависимостей (18, 19, 20):

;

;

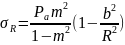где

;

.

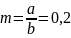
Полученные значения напряжений сводим в таблицу 1.

	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
	-1,697	-0,715	-0,371	-0,212	-0,126	-0,074	-0,039	-0,016	0
	1,839	0,856	0,513	0,354	0,267	0,215	0,181	0,158	0,141
	0,071	0,071	0,071	0,071	0,071	0,071	0,071	0,071	0,071

Таблица 1 – Результаты расчетов напряжений в пределах линейной упругости.

По данным расчетным значениям строим график распределения напряжения вдоль свода толстостенной трубы (Рисунок 3, Приложение 1).

3. Расчет напряжений в зоне пластического деформирования трубы для диаграммы материала с линейным упрочнением

Для определения напряжений в зоне пластического деформирования трубы для диаграммы материала с линейным упрочнением воспользуемся расчетными зависимостями (38):

;

;

.

Полученные значения напряжений сводим в таблицу 2.

Таблица 2 – Результаты расчетов напряжений в зоне пластического деформирования трубы.

	0,2	0,3	0,4	0,5	=0,6
	-1,698	-1,187	-0,842	-0,581	-0,369
	-0,377	0,03	0,338	0,583	0,785
	-1,038	-0,578	-0,252	0,001	0,208

По данным расчетным значениям строим график распределения напряжения вдоль свода толстостенной трубы (Рисунок 3, Приложение 1).

4. Расчет напряжений в зоне упругого деформирования трубы для диаграммы материала с линейным упрочнением

В зоне упругого деформирования трубы для определения напряжений воспользуемся расчетными зависимостями (40):

Таблица 3 – Результаты расчетов напряжений в зоне упругого деформирования трубы.

	=0,6	0,7	0,8	0,9	1
	-0, 369	-0,216	-0,117	-0,049	0
	0,785	0,632	0,533	0,464	0,416
	0,208	0,208	0,208	0,208	0,208

По полученным расчетным значениям строим график распределения напряжения вдоль свода толстостенной трубы (Рисунок 3, Приложение 1).