Федеральное агентство по образованию

Бийский технологический институт (филиал)

государственное образовательное учреждение

высшего профессионального образования

«Алтайский государственный технический университет

им. И.И. Ползунова»

Кафедра ТМ

Дисциплина: «Физические основы пластической деформации»

Расчетно-графическая работа

Методика и расчет распределения напряжений вдоль свода толстостенной трубы в условиях упругопластического деформирования при осесимметричном нагружении

Пояснительная записка

Выполнил: Студент гр. ВУАС-81 Серов В.А.

Проверил: проф. Казанцев В.Г.

Содержание

Раздел 1. Методика расчета напряженного состояния толстостенной

трубы в пределах и за пределами упругости 3

1. Вывод соотношений для оценки напряженно-деформирован-

ного состояния трубы 3

2. Соотношения для напряженного состояния трубы в пределах

упругости 7

3. Соотношения для напряженного состояния трубы при ее упругопластическом деформировании для диаграммы

деформирования с линейным упрочнением 9

Раздел 2. Расчет напряженного состояния толстостенной трубы в

пределах и за пределами упругости 13

1. Расчетная схема и исходные данные 13

2. Расчет напряжений в пределах линейной упругости 14

3. Расчет напряжений в зоне пластического деформирования

трубы для диаграммы материала с линейным упрочнением 15

4. Расчет напряжений в зоне упругого деформирования трубы

для диаграммы материала с линейным упрочнением 16

5. Анализ и обсуждение механического поведения толстостенной

трубы при ее деформировании в пределах и за пределами

упругости 17

Раздел 3. Методика расчета резерва прочности 18

3.1 Закон разгрузки и повторное нагружение. Резерв прочности 18

3.2 Расчет резерва прочности 21

Раздел 1. Методика расчета напряженного состояния толстостенной трубы в пределах и за пределами упругости

1. Вывод соотношений для оценки напряженно-деформированного состояния трубы

Рассмотрим решение задачи об упругопластическом напряженно-деформированном состоянии (НДС) полого толстостенного цилиндра, подверженного внутреннему давлению .

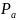Для осесимметричного нагружения в пределах упругости наиболее напряженной зоной цилиндра является область в виде кольца, примыкающего к его внутренней поверхности. Поэтому именно в этой области начинаю возникать пластические деформации, которые по мере увеличения давления развиваются в радиальном направлении вдоль свода сечения толстостенного цилиндра. Пусть степень развития пластических деформаций характеризуется некоторым радиусом , который отделяет пластическую и упругую области в радиальном сечении цилиндра, (рисунок 1. a)

Рисунок 1 - Упругопластическое состояние полого цилиндра.

Рассмотрим случай плоского деформированного состояния полого цилиндра 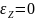, полагая материал цилиндра несжимаемым с некоторой известной, но достаточно произвольной диаграммой деформирования:

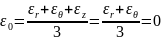; ; (1)

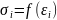, (2)

Силовая составляющая задачи – уравнение равновесие для элементарного объема цилиндра не зависит от механических свойств материала, поэтому соответствует уравнению:

. (3)

Интегрирую уравнение (3) получим:

, (4)

Заметим, что из третьего уравнения определяющих соотношений на основании (1) можно получить:

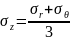, и (5)

Интенсивность напряжений для случая плоской деформации в полярных координатах с учетом зависимости (5) примет вид:

. (6)

При помощи связи (6) приведем соотношение (4) к виду:

. (7)

Для связи силовой (уравнение 7) и деформационной составляющих задачи, определим закон изменения интенсивности деформаций.

Примем во внимание, что геометрические соотношения Коши, справедливы как в условиях линейно-упругого деформирования материала, так и за пределами. В полярных системах координат соотношения Коши имеют следующие представления:

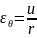; . (8)

Дифференциальное уравнение для радиальных перемещений u получим, использую зависимости (1):

.

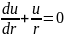Интеграл этого уравнения известен, имеет вид:

, (9)

где С – постоянная интегрирования.

В полярных координатах выражение для интенсивности деформаций в условиях плоской деформации , с учетом соотношений (1) примет вид:

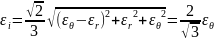. (10)

Со ссылкой на зависимости (8) и (9) из уравнения (10) получим:

. (11)

Дифференцируя соотношение (11) придем:

,

или 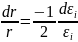(12)

Возвращаясь к соотношению (7), использую при этом выражение (12), для радиальных напряжений получим:

,

или с учетом (2) найдем:

. (13)

Окружные тангенциальные напряжения получим из соотношений (6) и (13):

. (14)

При помощи выражения (5) определим осевое напряжение:

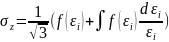. (15)

Таким образом, напряженное состояние полого толстостенного цилиндра определяется выражениями (13 – 15) при заданной диаграмме деформирования материала (2). Для продолжения решения задачи необходимо определиться с физическими свойствами материала цилиндра.

Рассмотрим напряженное состояние полого цилиндра под действием внутреннего давления для некоторых вариантов схематизации диаграммы деформирования материала – в виде линейного закона, линейного закона с линейным упрочнением и линейного закона со степенным упрочнением.